高中数学必修4教案：1_2_1任意角的三角函数(1)

高中数学必修4教案：1_2_1任意角的三角函数(1)

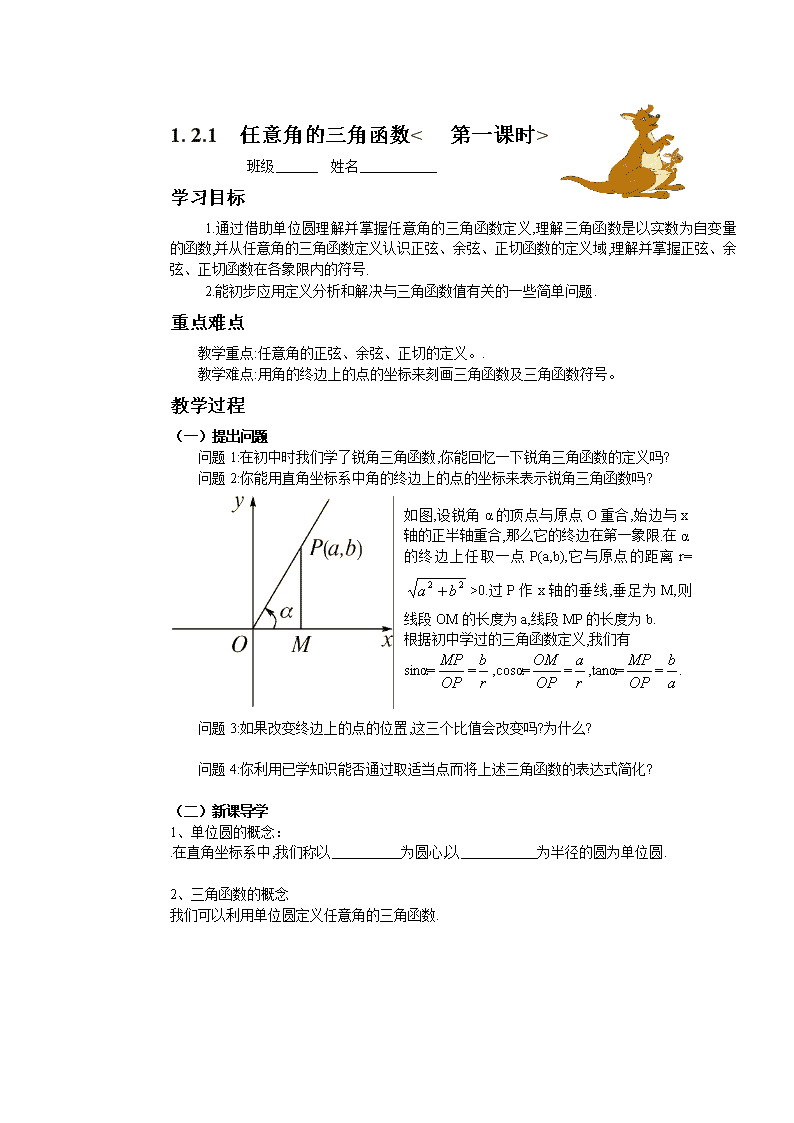
‎1. 2.1 任意角的三角函数< 第一课时>‎ 班级 姓名 ‎ 学习目标 ‎1.通过借助单位圆理解并掌握任意角的三角函数定义,理解三角函数是以实数为自变量的函数,并从任意角的三角函数定义认识正弦、余弦、正切函数的定义域,理解并掌握正弦、余弦、正切函数在各象限内的符号.‎ ‎ 2.能初步应用定义分析和解决与三角函数值有关的一些简单问题.‎ 重点难点 教学重点:任意角的正弦、余弦、正切的定义。.‎ 教学难点:用角的终边上的点的坐标来刻画三角函数及三角函数符号。‎ 教学过程 ‎（一）提出问题 ‎ 问题1:在初中时我们学了锐角三角函数,你能回忆一下锐角三角函数的定义吗?‎ ‎ 问题2:你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗?‎ 如图,设锐角α的顶点与原点O重合,始边与x轴的正半轴重合,那么它的终边在第一象限.在α的终边上任取一点P(a,b),它与原点的距离r=>0.过P作x轴的垂线,垂足为M,则线段OM的长度为a,线段MP的长度为b.‎ 根据初中学过的三角函数定义,我们有 sinα==,cosα==,tanα==.‎ 问题3:如果改变终边上的点的位置,这三个比值会改变吗?为什么?‎ 问题4:你利用已学知识能否通过取适当点而将上述三角函数的表达式简化?‎ ‎（二）新课导学 ‎1、单位圆的概念：‎ ‎.在直角坐标系中,我们称以 为圆心,以 为半径的圆为单位圆.‎ ‎2、三角函数的概念 我们可以利用单位圆定义任意角的三角函数.‎ 图2‎ ‎ 如图2所示,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:‎ ‎(1)y叫做α的正弦,记作sinα,即sinα=y;‎ ‎ (2)x叫做α的余弦,记作cosα,即cosα=x;‎ ‎(3)叫做α的正切,记作tanα,即tanα=(x≠0).‎ 所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数.‎ 注意:(1)正弦、余弦、正切、都是以角为自变量,以比值为函数值的函数.‎ ‎(2)sinα不是sin与α的乘积,而是一个比值;三角函数的记号是一个整体,离开自变量的“sin”“tan”等是没有意义的.‎ ‎（3）由相似三角形的知识,对于确定的角α,这三个比值不会随点P在α的终边上的位置的改变而改变.‎ ‎3、例1：已知角α的终边与单位圆的交点是 求角α的正弦、余弦和正切值。‎ ‎ ‎ 练习1：已知角α的终边经过点 ，求角α正弦、余弦和正切值。‎ 例2 求 的正弦、余弦和正切值.‎ 练习2：用三角函数的定义求 的三个三角函数值 ‎4、定义推广：‎ 设角是一个任意角，P（x,y）是其终边上的任意一点，‎ 点P与原点的距离 那么① 叫做的正弦，即 ‎ ② 叫做的余弦，即 ‎③ 叫做的正切，即 ‎4、 探究 .三角函数的定义域 三角函数 定义域 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎5、例题讲解 例3 已知角的终边经过点P(-3,-4)，求角的正弦、余弦和正切值 .‎ 练习3. 已知角的终边过点P(-12,5) ,求的正弦、余弦和正切三个三角函数值.‎ ‎5、探究三角函数值在各象限的符号 ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎（ ） ）‎ ‎6、例题讲解 例4、 求证:当且仅当下列不等式组成立时,角θ为第三象限角.反之也对。‎ 变式训练 ‎（1、） (2007北京高考)已知cosθ·tanθ<0,那么角θ是( )‎ A.第一或第二象限角 B.第二或第三象限角 C.第三或第四象限角 D.第一或第四象限角 ‎（2、）教材第15页第6题 ‎（三）课堂小结 知识 ‎ ‎ 能力 ‎ ‎（四）作业布置 习题1.2A组第2,9题