- 2021-07-01 发布 |
- 37.5 KB |
- 7页
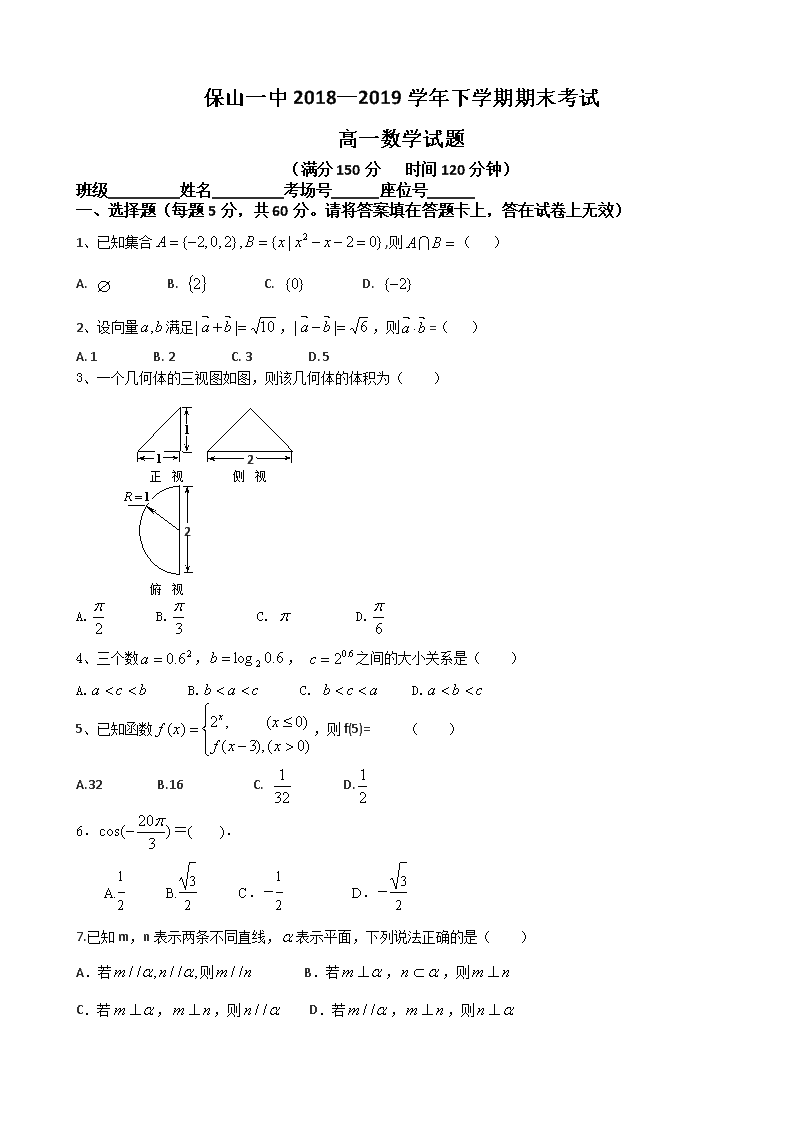

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年云南省保山市第一中学高一下学期期末考试数学试题
保山一中2018—2019学年下学期期末考试 高一数学试题 (满分150分 时间120分钟) 班级_________姓名_________考场号______座位号______ 一、选择题(每题5分,共60分。请将答案填在答题卡上,答在试卷上无效) 1、已知集合,则( ) A. B. C. D. 2、设向量满足,,则=( ) A. 1 B. 2 C. 3 D. 5 3、一个几何体的三视图如图,则该几何体的体积为( ) 侧视图 正视图 俯视图 2 2 A. B. C. D. 4、三个数,, 之间的大小关系是( ) A. B. C. D. 5、 已知函数,则f(5)= ( ) A.32 B.16 C. D. 6.=( ). A. B. C.- D.- 7.已知m,n表示两条不同直线,表示平面,下列说法正确的是( ) A.若则 B.若,,则 C.若,,则 D.若,,则 8、已知函数在[1,2]上的最大值与最小值之和为,则的值为 ( ) A.2 B.4 C. D. 9、为了得到函数的图象,可以将函数的图象( ) A.向右平移个单位长 B.向右平移个单位长 C.向左平移个单位长 D.向左平移个单位长 10、 ,则 ( ) A. B. C. D. 11、函数y=cos2x-2sinx+1的最大值是 ( ) A.-2 B.2 C. D. 12、方程的实根个数为( ) A.6 B.7 C.8 D.9 二、填空题(每题5分,共20分,请将答案填在答题卡上,答在试卷上无效) 13、在平行四边形中,对角线与交于点,,则_____; 14、已知正方形ABCD的边长为2,E为BC的 中点,则________. 15、 执行右侧的程序框图,若输入,则输出 16. 已知函数,则下列四个结论中正确的有________个; ①y=f(x)的图象关于点对称;②y=f(x)的图象关于直线对称; ③y=f(x)在上是增函数;④当时,f(x)的值域为。 三、解答题(第17题10分,其余每题12分,共70分。请将答案填在答题卡上,答在试卷上无效) 17、已知点A(1,-1),B(5,1),直线经过点A,且斜率为, (Ⅰ)求直线的方程; (Ⅱ)求以B为圆心,并且与直线相切的圆的标准方程。 18.假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料: 2 3 4 5 6 y 2.2 3.8 5.5 6.5 7.0 若由资料知,y对x呈线性相关关系,试求: (Ⅰ)请根据上表提供的数据,求出y关于x的线性回归方程; (Ⅱ)估计使用年限为10年时,维修费用约是多少? () 19、已知向量, 设函数. (Ⅰ) 求f (x)的最小正周期. (Ⅱ) 求f (x)的单调递增区间。 20、 从某企业生产的某种产品中抽取20件,测量这些产品的一项质量指标值,由测量得到如图的频率分布直方图,从左到右各组的频数依次记为; i = i +1 开始 结束 否 输出S i<5? 是 S=0,i = 2 (Ⅰ)求图中的值; (Ⅱ)下图是统计图中各组频数的一个算法流程图,求输出的结果S; (Ⅲ)在样本中从质量指标值分布在[80,90)、[110,120)的产品中随机抽取2件产品,求所抽取两件产品的质量指标值之差大于10的概率. 20、 如图:在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AD=AC=AB=DE=1, ∠DAC=90°,F是CD的中点. (Ⅰ)求证:AF∥平面BCE; (Ⅱ)求点D到平面BCE的距离. 22、 若的最大值为m,且直线y=m与y=f(x)的图像相邻两交点的横坐标相差个单位。 (1) 求和m的值; (2) 已知,求的值。 保山一中2018—2019学年下学期期末考试 高一数学参考答案 一、选择题(本大题共12小题,每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A D B D C B A A D C C 二、 填空题(本大题共4小题,每小题5分,共20分) 13、 2 14、 -2 15、7 16、 3 三、 解答题(第17题10分,其余每题12分,共70分) 17、解:(1)直线的方程为 即 (2) 所以圆B的方程为 18、 解:(1), y关于x的线性回归方程为 (2) 当x=10时, 所以使用年限为10年时,维修费用约是12.38万元。 19、 解: (1) (2) 令 20、 解:(1) (2) (3)质量指标在[80,90)的产品有件,记为a; 质量指标在[110,120)的产品有件,记为1,2,3,4 则从5件产品中任取2件产品的基本事件有 (a,1),(a,2),(a,3),(a,4),(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共10个,记事件A为所抽取的两件产品的质量指标值之差大于10,则事件A包含的基本事件有(a,1),(a,2),(a,3),(a,4)共4个, 21、解:(1)取取CE的中点M,连结MF,MB, ∵F是CD的中点 ∵AB⊥平面ACD,DE⊥平面ACD ∴AB∥DE,∵AB=DE ∴四边形ABMF是平行四边形 AF∥BM,又AF平面BCE,BM平面BCE ∴AF∥平面BCE (2) ,, , 记点D到平面BCE的距离为d 点D到平面BCE的距离为 解:(1) (2) 查看更多