2020长春地区高三一模(文数)答案

2020长春地区高三一模(文数)答案

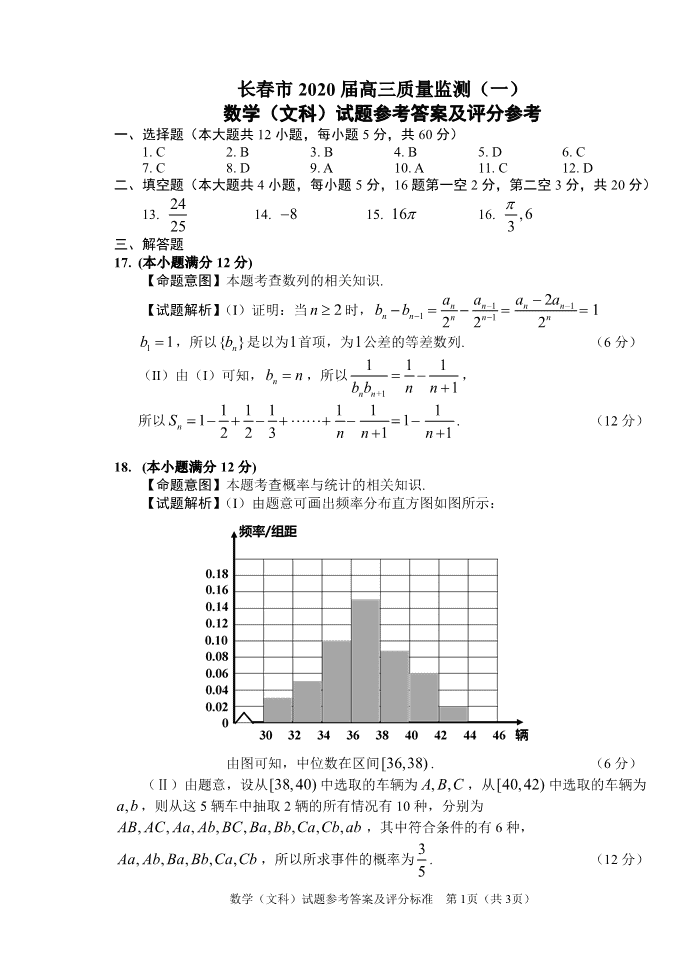
数学（文科）试题参考答案及评分标准 第 1页（共 3页） 长春市 2020 届高三质量监测（一） 数学（文科）试题参考答案及评分参考 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分） 1. C 2. B 3. B 4. B 5. D 6. C 7. C 8. D 9. A 10. A 11. C 12. D 二、填空题（本大题共 4 小题，每小题 5 分，16 题第一空 2 分，第二空 3 分，共 20 分） 13. 24 25 14. 8 15. 16 16. ,63  三、解答题 17. (本小题满分 12 分) 【命题意图】本题考查数列的相关知识. 【试题解析】（Ⅰ）证明：当 2n  时， 1 1 1 1 2 12 2 2 n n n n n n n n n a a a ab b          1 1b  ，所以{ }nb 是以为1首项，为1公差的等差数列. （6 分） （Ⅱ）由（Ⅰ）可知， nb n ，所以 +1 1 1 1 1n nb b n n    ， 所以 1 1 1 1 1 11 12 2 3 1 1nS n n n           . （12 分） 18. (本小题满分 12 分) 【命题意图】本题考查概率与统计的相关知识. 【试题解析】（Ⅰ）由题意可画出频率分布直方图如图所示： 由图可知，中位数在区间[36,38) . （6 分） （Ⅱ）由题意，设从[38,40) 中选取的车辆为 , ,A B C ，从[40,42) 中选取的车辆为 ,a b ，则从这 5 辆车中抽取 2 辆的所有情况有 10 种，分别为 , , , , , , , , ,AB AC Aa Ab BC Ba Bb Ca Cb ab ，其中符合条件的有 6 种， , , , , ,Aa Ab Ba Bb Ca Cb ，所以所求事件的概率为 3 5 . （12 分） 数学（文科）试题参考答案及评分标准 第 2页（共 3页） 19. (本小题满分 12 分) 【命题意图】本题考查立体几何的相关知识. 【试题解析】（Ⅰ）证明：在 ABC 内取一点 P ，作 ,PD AC PE BC  ， 因为平面 ABC  平面 1 1ACC A ，其交线为 AC ，所以 PD  平面 1 1ACC A ， 1PD CC ， 同理 1PE CC ，所以 1CC  平面 ABC ， 1 1,CC AC CC BC  ， 同理 AC BC ，故 1, ,CC AC BC 两两垂直. （6 分） （Ⅱ）由（Ⅰ）可知，三棱锥 1 1A BCB 的高为 1 1AC a ， 1 2 1 1 1 2 2BCBS BC BB a    ，所以三棱锥 1 1B A BC 的体积为 31 6 a . （12 分） 20. (本小题满分 12 分) 【命题意图】本小题考查圆锥曲线中的最值问题等知识. 【试题解析】解：（Ⅰ）由定义法可得， P 点的轨迹为椭圆且 2 4a  ， 1c  . 因此椭圆的方程为 2 2 14 3 x y  . （4 分） （Ⅱ）设直线l 的方程为 3x ty  与椭圆 2 2 14 3 x y  交于点 1 1( , )A x y ， 2 2( , )B x y ，联立直线与椭圆的方程消去 x 可得 2 2(3 4) 6 3 3 0t y ty    ，即 1 2 2 6 3 3 4 ty y t    ， 1 2 2 3 3 4y y t   . AOB 面积可表示为 2 1 2 1 2 1 2 1 1| | | | 3 ( ) 42 2AOBS OQ y y y y y y       △ 2 2 2 2 2 2 2 2 1 6 3 3 3 2 3 63 ( ) 4 9 3 4 3 12 3 4 3 4 2 3 4 3 4 t t t tt t t t                令 23 1t u  ，则 1u ≥ ，上式可化为 2 6 6 333 u u u u   ≤ ， 当且仅当 3u  ，即 6 3t   时等号成立， 因此 AOB 面积的最大值为 3 ，此时直线l 的方程为 6 33x y   . （12 分） 21. (本小题满分 12 分) 【命题意图】本小题考查函数与导数的相关知识. 【试题解析】解：（Ⅰ）令 2 1( ) 0xf x x    ， 1x  （2 分） x (0,1) 1 (1, ) ( )f x  0 + ( )f x  极小值  ( ) = (1) 2f x f 极小值 ，无极大值； （4 分） 数学（文科）试题参考答案及评分标准 第 3页（共 3页） （II）由题意可知， 0a  ，则原不等式等价于 2 ( 1) ln 01 a x xx    ， 令 2 ( 1)( ) ln (0 1)1 a xg x x xx     ， 2 2 ( (2 4 ) 1)( ) ( 1) x a xg x x x       ， ①当 0 1a  时， 2 (2 4 ) 1 0x a x    ， ( ) 0g x  ， ( )g x 在 (0,1) 上单调递减， ( ) (1) 0g x g  ，成立； ②当 1a  时， 2 0 0 0(0,1), (2 4 ) 1 0x x a x      ，使得当 0(0, )x x 时， ( ) 0g x  ， ( )g x 单调递减，当 0( ,1)x x 时， ( ) 0g x  ， ( )g x 单调递增，故当 0( ,1)x x 时， ( ) (1) 0g x g  ，不成立；综上所述， 0 1a  . （12 分） 22. (本小题满分 10 分) 【命题意图】本小题主要考查极坐标与参数方程的相关知识. 【试题解析】解：（Ⅰ）直线l 的普通方程为 3 0x y   ， 圆C 的直角坐标方程为 2 2 4 3 0x y x    . （5 分） （Ⅱ）联立直线l 的参数方程与圆C 的直角坐标方程可得 2 22 2 2(1 ) (2 ) 4(1 ) 3 02 2 2t t t       ，化简可得 2 3 2 2 0t t   . 则 1 2| | | | | | 2PA PB t t   . （10 分） 23. (本小题满分 10 分) 【命题意图】本小题主要考查不等式的相关知识. 【试题解析】（Ⅰ）由题意 ( 3) (1 ) 3 4 3 ( ) ( 3) (1 ) 3 1 2 2 3 1 ( 3) ( 1) 1 4 1 x x x x f x x x x x x x x x x                                ≤ ≤ ≤ ≤ 当 3x   时， 4 1x ≥ ，可得 5x ≤ ，即 5x ≤ . 当 3 1x ≤ ≤ 时， 2 2 1x x ≥ ，可得 1x ≥ ，即 1 1x ≤ ≤ . 当 1x  时， 4 1x ≥ ，可得 3x ≤ ，即1 3x ≤ . 综上，不等式 ( ) 1f x x ≥ 的解集为 ( , 5] [ 1,3]   . （5 分） （Ⅱ）由（Ⅰ）可得函数 )(xf 的最大值 4M  ，且 1 4ab a b    ， 即 23 ( ) ( )2 a ba b ab    ≤ ，当且仅当 a b 时“=”成立， 可得 2( 2) 16a b  ≥ ，即 2a b ≥ ，因此 ba  的最小值为 2. （10 分）