山西省实验中学2019-2020高三3月开学摸底考试数学（文）试卷

山西省实验中学2019-2020高三3月开学摸底考试数学（文）试卷

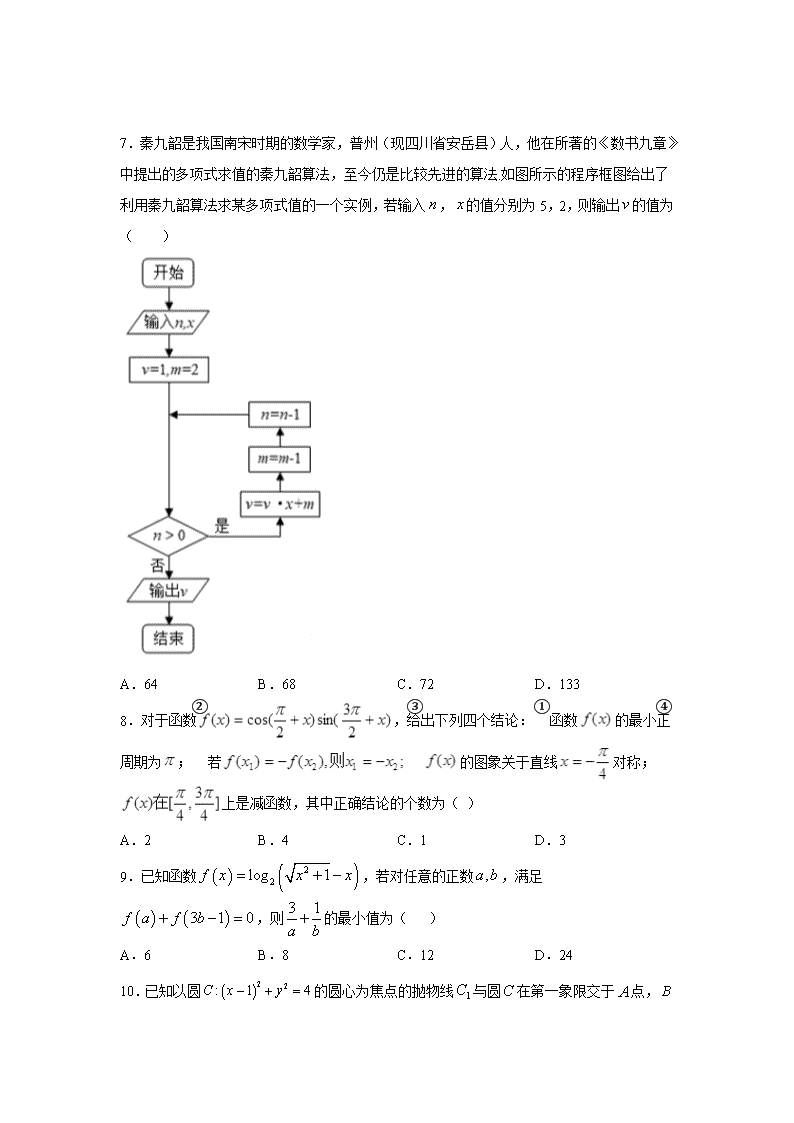
数 学 试 题 （文史类 A 卷） 注意事项： 1. 本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。 2. 答题前，考生务必将自己的姓名、准考证号填写在相应位置。 3. 全部答案在答题卡上完成，答在本试卷上无效。 4. 考试结束后，将本试题和答题卡一并交回。 第 I 卷 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的） 1．设集合 ， ，则 （ ） A． B． C． D． 2．已知 是虚数单位，则复数 的共轭复数的虚部是（ ） A． B． C． D．1 3．向量 （1，﹣2）， （2，﹣1），则 （　 　） A．9 B．11 C．13 D．15 4．已知各项均为正数的等比数列 的前 项和为 ，且满足 ， ， 成等差数列， 则 ( ) A．3 B．9 C．10 D．13 5．现有甲班 三名学生，乙班 两名学生，从这 名学生中选 名学生参加某项 活动，则选取的 名学生来自于不同班级的概率是（ ） A． B． C． D． 6．函数 的图象大致为( ) A． B． C． D． { }2|log 1M x x= < { }2| 2 0N x x x= + − > RM N = ( 2,2)− [ 2,2)− (0,1] (0,1) i 4 3 3 4 iz i += − i− i 1− a = b = ( )2a b a+ ⋅   = { }na n nS 6a 43a 5a− 4 2 S S , ,A B C ,D E 5 2 2 1 5 3 10 2 5 3 5 1 ln sin1 ln xy xx −= ⋅+ 7．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》 中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了 利用秦九韶算法求某多项式值的一个实例，若输入 ， 的值分别为 5，2，则输出 的值为 （ ） A．64 B．68 C．72 D．133 8．对于函数 ，给出下列四个结论：①函数 的最小正 周期为 ；②若 ③ 的图象关于直线 对称；④ 上是减函数，其中正确结论的个数为（ ） A．2 B．4 C．1 D．3 9．已知函数 ，若对任意的正数 ，满足 ，则 的最小值为（ ） A．6 B．8 C．12 D．24 10．已知以圆 的圆心为焦点的抛物线 与圆 在第一象限交于 点， n x v ( ) ( )2 2log 1f x x x= + − ,a b ( ) ( )3 1 0f a f b+ − = 3 1 a b + ( )2 2: 1 4C x y− + = 1C C A B 点是抛物线： 上任意一点， 与直线 垂直，垂足为 ，则 的最大值为( ) A．1 B．2 C． D．8 11．如图，正方体 的对角线 上存在一动点 ，过点 作垂直于平面 的直线，与正方体表面相交于 两点.设 ， 的面积为 ，则当 点 由点 运动到 的中点时，函数 的图象大致是（ ） A． B． C． D． 12．已知 ，若不等式 在 上有解，则实数 的取值范围是（ ） A． B． C． D． 第 II 卷（非选择题，共 90 分） 本卷包括必考题和选考题两部分，第 13 题~第 21 题为必考题，每个试题 考生都必须作答.第 22 题~第 23 题为选考题，考生根据要求作答. 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分） 13．若实数 满足约束条件 ，则 的最小值是____. 14．已知点 分别是圆 及直线 上的动点， 是 坐标原点则 最小值为_____. 2 :C 2 8x y= BM 2y = − M BM AB− 1− 1 1 1 1ABCD A B C D− 1BD P P 1 1BB D D ,M N BP x= BMN∆ S P B 1BD ( )S f x= ( ) ( )x xf x x e e−= − ( ) ( )1 2f ax f x- > - [ ]3,4x∈ a ( ) 2- 0 3  ∞ ∪ + ∞  ， ， 1 2- - 4 3    ∞ ∪ + ∞      ， ， 1 3- - 4 4    ∞ ∪ + ∞      ， ， ( ) 3- 0 4  ∞ ∪ + ∞  ， ， ,x y 4 1 0, 1 4 x y y x y − − ≥  ≥  + ≤ ln lnz y x= − ,P Q 2 2: ( 2) ( 1) 1C x y+ + − = :3 4 0l x y− = O | |OP OQ−  15．若侧面积为 的圆柱有一外接球 O，当球 O 的体积取得最小值时，圆柱的表面积为 _______. 16．已知数列 的前 项和 ，若不等式 ，对 恒成立，则整数 的最大值为______． 三、解答题：解答应写出文字说明，证明过程或演算步骤。 17．（本小题满分 12 分） 在 中，角 A，B，C 对边分别为 ， ， ，且 是 与 的等 差中项. （1）求角 A； （2）若 ，且 的外接圆半径为 1，求 的面积. 18.（本小题满分 12 分） 《汉字听写大会》不断创收视新高，为了避免“书写危机”，弘扬传统文化，某市大约 10 万 名市民进行了汉字听写测试.现从某社区居民中随机抽取 50 名市民的听写测试情况，发现被 测试市民正确书写汉字的个数全部在 160 到 184 之间，将测试结果按如下方式分成六组： 第 1 组 ，第 2 组 ，…，第 6 组 ，如图是按上述分组方法得 到的频率分布直方图. { }na n 12 2n n nS a += − 22 3 (5 ) nn n aλ− − < − n N +∀ ∈ λ ABC∆ a b c sin 2c A π −   cosa B cosb A 2a b c= + ABC∆ ABC∆ [ )160,164 [ )164,168 [ ]180,184 （1）若电视台记者要从抽取的市民中选 1 人进行采访，求被采访人恰好在第 2 组或第 6 组 的概率； （2）试估计该市市民正确书写汉字的个数的众数与中位数； （3）已知第 4 组市民中有 3 名男性，组织方要从第 4 组中随机抽取 2 名市民组成弘扬传统 文化宣传队，求至少有 1 名女性市民的概率. 19.（本小题满分 12 分） 如图，已知四棱锥 P-ABCD 的底面是边长为 的菱形， ，点 E 是棱 BC 的 中点， ，点 P 在平面 ABCD 的射影为 O，F 为棱 PA 上一点． (1)求证：平面 PED 平面 BCF； (2)若 BF//平面 PDE，PO=2，求四棱锥 F-ABED 的体积． 2 3 60BAD∠ =  DE AC O∩ = ⊥ 20. （本小题满分 12 分） 已知 是椭圆 的左右顶点， 点为椭圆 上一点，点 关于 轴的对称点为 ，且 . （1）若椭圆 经过圆 的圆心，求椭圆 的方程； （2）在（1）的条件下，若过点 的直线与椭圆 相交于不同的 两点，设 为椭 圆 上一点，且满足 （ 为坐标原点），当 时，求实数 的取值 范围. 21. (本小题满分 12 分) 已知函数 ， ， 在点 处的切线与 轴平行. （1）求 的单调区间； （2）若存在 ，当 时，恒有 成立，求 的取 值范围. 请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一题计分。 ,Q R 2 2 2 2: 1( 0)x yC a ba b + = > > P C P x H 1 2PQ RHk k⋅ = C 2 2( 1) 4x y+ − = C (2,0)M C ,A B P C OA OB tOP+ =   O 2 5| | 3AB < t ( ) ( )ln 1f x x a x= − + a R∈ ( )f x ( )( )1, 1f x ( )f x 0 1x > ( )01,x x∈ ( ) ( )2 12 12 2 xf x x k x− + + > − k 22. 在平面直角坐标系 中，曲线 的参数方程为 为参数），以坐标原点 为极点， 轴的正半轴为极轴建立极坐标系，并使得它与直角坐标系 有相同的长度单 位，直线 的直角坐标方程为 ． （1）求曲线 的极坐标方程； （2）若曲线 的极坐标方程为 ，与直线 在第三象限交于 点，直线 与 在第一象限的交点为 ，求 ． 23. 已知函数 （1）当 时，求不等式 的解集； （2）对于任意的实数 ，存在实数 ，使得不等式 成立，求实数 的 取值范围。 xOy 1C cos (2sin x t ty t =  = x xOy l 3y x= 1C 2C 8cos 0ρ θ+ = l A l 1C B AB ( ) | | | 2 2 | ( 0)f x x m x m x= + − − > 1 2m = 1( ) 2f x ≥ x t ( ) | 3| | 4 |f x t t+ − < + m 参考答案 1．B 【解析】 【分析】 求出集合 ，再由集合的运算计算． 【详解】 由题意 ， ， ∴ ， ， ， ∴ ． 故选：B. 【点睛】 本题考查集合的运算，考查解对数不等式及一元二次不等式，掌握对数函数的性质是解题关 键． 2．C 【解析】 【分析】 由复数除法求出复数 ，再写出共轭复数，得其虚部． 【详解】 由题意 ， ，虚部为 ． 故选：C. 【点睛】 本题考查复数的除法运算，考查共轭复数的概念及复数的概念．解题关键是掌握复数除法法 则． 3．C 【解析】 【分析】 先得出 ，再根据向量数量积的坐标表示即可得解. ,M N 2log 1 0 2x x< ⇒ < < 2 2 0 ( 1)( 2) 0 2 1x x x x x+ − > ⇒ − + > ⇒ − < < (0,2)M = ( , 2) (1, )N = −∞ − +∞ 2{ | 2 0} [ 2,1]R N x x x= + − ≤ = − ( ) [ 2,2)RM N = −  z 24 3 (4 3 )(3 4 ) 12 16 9 12 3 4 (3 4 )(3 4 ) 25 i i i i i iz ii i i + + + + + += = = =− − + z i= − 1− ( )2 5, 4a b+ = −  【详解】 由题意 ，则 . 故选：C. 【点睛】 本题考查了向量线性运算的坐标表示和向量数量积的坐标表示，属于基础题. 4．C 【解析】 【分析】 设 的公比为 ，由 成等差数列，可得 ，解得 ， 再利用求和公式即可得结果. 【详解】 设各项均为正数的等比数列 的公比为 ， 满足 成等差数列， ， ，解得 ， 则 ，故选 C. 【点睛】 本题主要考查等比数列的通项公式与求和公式，属于中档题. 等比数列基本量的运算是等比 数列的一类基本题型，数列中的五个基本量 ，一般可以“知二求三”，通过列 方程组所求问题可以迎刃而解，解决此类问题的关键是熟练掌握等比数列的有关性质和公式， 并灵活应用，在运算过程中，还应善于运用整体代换思想简化运算过程. 5．D 【解析】 【详解】 解：从这 名学生中选 名学生参加某项活动， ( )2 5, 4a b+ = −  ( ) ( ) ( )2 5 1 4 2 13a b a+ ⋅ = × + − × − =   { }na 0q > 6 4 5,3 ,a a a− 2 6 0, 0q q q− − = > q { }na 0q >  6 4 5,3 ,a a a− ( )2 4 6 5 4 46 , 6 , 0a a a a a q q q∴ = − ∴ = − > 2 6 0, 0q q q∴ − − = > 3q = ( ) ( ) 4 1 24 2 2 1 3 1 3 1 3 1 10 3 1 3 1 a S S a − −= = + = − − 1, , , , ,n na q n a S 5 2 基本事件总数 n 10， 抽到 2 名学生来自于同一班级包含的基本事件个数 m 4， ∴抽到 2 名学生来自于不同班级的概率是 P ． 故选 D 【点睛】 本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，考查函数 与方程思想，是基础题． 6．A 【解析】 设 ，由 得 ，则函数的定义域为 ． ∵ ， ∴函数 为奇函数，排除 D． 又 ，且 ，故可排除 B． ，且 ，故可排除 C．选 A． 7．B 【解析】 【分析】 根据已知的程序框图可得，该程序的功能是利用循环结构计算并输出变量 v 的值，模拟程序 的运行过程，可得答案． 【详解】 模拟程序的运行，可得： n＝5，x＝2， 2 5C= = 2 2 3 2C C= + = 4 31 1 10 5 m n = − = − = 1 ln( ) sin1 ln xf x xx −= ⋅+ 1 ln 0x+ ≠ 1x e ≠ ± 1 1 1 1( , ) ( , ) ( , )e e e e −∞ − ∪ − ∪ +∞ 1 ln 1 ln( ) sin( ) sin ( )1 ln 1 ln x xf x x x f xx x − − −− = ⋅ − = − ⋅ = −+ − + ( )f x 11 e > (1) sin1>0f = 2 1 1 e e < 2 2 2 2 2 11 ln 1 1 ( 2) 1 1( ) sin sin 3 sin 01 1 21 ln ef x e e e e − − −= ⋅ = ⋅ = − ⋅ <−+ v＝1，m＝2， 满足进行循环的条件 n＞0，执行循环体，v＝ 4，m＝1，n＝4， 满足进行循环的条件 n＞0，执行循环体，v＝ 9，m＝0，n＝3， 满足进行循环的条件 n＞0，执行循环体，v＝ 18，m＝﹣1，n＝2， 满足进行循环的条件 n＞0，执行循环体，v＝ 35，m＝﹣2，n＝1， 满足进行循环的条件 n＞0，执行循环体，v＝ 68，m＝﹣3，n＝0， 不满足进行循环的条件 n＞0，退出循环，输出 v 的值为 68． 故选：B． 【点睛】 本题考查的知识点是程序框图，当循环次数不多，或有规律可循时，可采用模拟程序法进行 解答，属于基础题． 8．D 【解析】 解：根据题意得：函数 =（-sinα）•（-cosα）=sinαcosα= sin2α， ①根据周期公式可得：f（x）= sin2x 的周期为 π．所以①正确； ②f（π 6 ）=-f（2π 3 ），但是不满足 x1=-x2，所以②错误； ③f（x）= sin2x 的所有对称轴为 x=kπ 2 +π 4 ，显然③正确； ④f（x）= sin2x 的单调减区间为[kπ+π 4 ，kπ+3π 4 ]，（k∈Z），显然④正确， 则其中正确结论的个数为 3． 故选 D 9．C 【解析】 【分析】 先确定函数奇偶性与单调性，再根据奇偶性与单调性化简方程得 ，最后根据基本 不等式求最值. 【详解】 因为 所以定义域为 ， 1 2 2× + = 4 2 1× + = 9 2 0× + = 18 2 1× − = 35 2 2× − = 1 2 1 2 ÷ ÷ 1 2 ÷ ÷ 1 2 ÷ ÷ 3 1a b+ = 2 21 0,x x x x x x+ − > − ≥ − = R 因为 ，所以 为减函数 因为 ， ,所以 为奇函数， 因为 ，所以 ，即 ， 所以 ， 因为 ， 所以 （当且仅当 ， 时，等号成立），选 C. 【点睛】 本题考查函数奇偶性与单调性以及基本不等式求最值，考查基本分析求解能力，属中档题. 10．A 【解析】 分析：由圆的标准方程求得圆心，可得抛物线 方程，利用运用抛物线的定义可得 ，从而可得结果. 详解：因为 的圆心 所以，可得以 为焦点的抛物线方程为 ， 由 ，解得 ， 抛物线 的焦点为 ，准线方程为 ， 即有 ， 当且仅当 在 之间）三点共线，可得最大值 ，故选 A. 点睛：本题主要考查抛物线的定义和几何性质，以及平面向量的数量积公式，属于难题.与 焦点、准线有关的问题一般情况下都与拋物线的定义有关，解决这类问题一定要注意点到点 ( ) 2 2 1log 1 f x x x = + + ( )f x ( ) 2 2 1log 1 f x x x = + + ( ) ( )2 2log 1f x x x− = + + ( ) ( ) ( )f x f x f x= − − ， ( ) ( )3 1 0f a f b+ − = ( ) ( )1 3 1 3f a f b a b= − = −， 3 1a b+ = ( )3 1 3 1 93 6b aa ba b a b a b  + = + + = + +   9 92 6b a b a a b a b + ≥ × = 3 1 12a b + ≥ 1 2a = 1 6b = 1C 1BM AB BF AB AF− = − ≤ = ( )2 2: 1 4C x y− + = ( )1,0 ( )1,0 2 4y x= ( ) 2 2 2 4 1 4 y x x y  = − + = ( )1,2A 2 2 : 8C x y= ( )0,2F 2y = − 1BM AB BF AB AF− = − ≤ = , , (A B F A ,B F 1 的距离与点到直线的距离的转化：（1）将抛线上的点到准线距离转化为该点到焦点的距离； (2)将抛物线上的点到焦点的距离转化为到准线的距离，使问题得到解决. 11．D 【解析】 设 ，而 由 运动到 的中点的过程中， ， 由相似三角形，可知 为定值，设正方体的边长为 ，当 为线段 的中点时， ，则 的面积为 ，故选 D. 12．A 【解析】 【分析】 利用导数分析函数单调性，再利用单调性求解不等式即可. 【详解】 因为 在区间 上 故 是增函数，又 ，则该函数为偶函数， 则不等式 等价于 在 有解 等价于 在区间 有解 即： 或 等价于 ，或 在区间 有解 等价于 或 2MN y= P B 1BD tan1 2 BP BP x BMPMP yMN = = = ∠ tan BMP∠ a P 1BD 3 62tan 22 2 a BMP a ∠ = = 6 ,3y x BMN= ∆ 1 2S MN BP= × × ( )2 21 2 6 6 02 3 3 x x x= × = > ( ) ( )x x x xf x e e x e e− −= − + +′ [ ]3,4 ( ) 0f x′ > ( )f x ( ) ( )f x f x= − ( ) ( )1 2f ax f x- > - 1 2ax x− > − [ ]3,4区间 1 2ax x− > − [ ]3,4 1 2ax x− > − 1 2ax x− < − 11a x > − 3 1a x < − [ ]3,4 11 min a x  > −   3 1 max a x  < −   解得 或 故 故选：A. 【点睛】 本题考查利用函数单调性奇偶性解不等式，涉及用导数判断函数单调性. 13．－ln3 【解析】 【分析】 由约束条件作出可行域，目标函数 z＝lny﹣lnx＝ln ，由图求出 的最大值即可． 【详解】 由实数 x，y 满足约束条件 作出可行域如图所示，联立 ，解得 B （3,1）， 由目标函数 z＝lny﹣lnx＝ln ，而 的最小值为 ＝ ，∴z＝lny﹣lnx 的最小值是 ﹣ln3． 故答案为﹣ln3． 【点睛】 本题考查简单的线性规划，考查了数形结合的解题思想方法，属于中档题． 14．1 【解析】 2 3a > 0a < ( ) 2,0 ,3a  ∈ −∞ ∪ +∞   y x y x 4 1 0, { 1 4 x y y x y − − ≥ ≥ + ≤ 4{ 1 x y y + = = y x y x OBk 1 3 【分析】 因为 ，表示圆上的点到直线上点的距离，要求最小值，则转化为圆上的点 到直线的距离，为此最小值即为圆心到直线的距离减去半径，所以再求圆心到直线的距离即 可. 【详解】 因为 ，表示两点间的距离， 又因为 分别是圆 及直线 上的动点， 所以 的最小值为圆心到直线的距离减半径， 圆心到直线的距离 所以圆上的点到直线的最小值为 所以 最小值为 1 故答案为：1 【点睛】 本题主要考查了向量模的几何意义和直线与圆的位置关系，还考查了数形结合的思想和运算 求解的能力，属于中档题. 15． 【解析】 【分析】 设圆柱的底面圆的半径为 ，高为 ，则球的半径 ，由圆柱的侧面积，求得 ， 得出 ，得到 得最小值，进而求得圆柱的表面积. 【详解】 由题意，设圆柱的底面圆的半径为 ，高为 ，则球的半径 . 因为球体积 ，故 最小当且仅当 最小. 圆柱的侧面积为 ，所以 ，所以 ，所以 ， 当且仅当 时，即 时取“=”号，此时 取最小值， | | | |− =  OP OQ QP | | | |− =  OP OQ QP ,P Q 2 2: ( 2) ( 1) 1C x y+ + − = :3 4 0l x y− = | | | |− =  OP OQ QP 10 25d = = 1d r− = | |OP OQ−  所以 ,圆柱的表面积为 . 【点睛】 本题主要考查了球的体积公式，以及圆柱的侧面公式的应用，其中解答中根据几何体的结构 特征，得出求得半径和圆柱的底面半径的关系式，求得圆柱的底面半径是解答的关键，着重 考查了空间想象能力，以及推理与运算能力，属于中档试题. 16．4 【解析】 【详解】 当 时， ，得 ， 当 时， ， 又 ， 两式相减得 ，得 ， 所以 ． 又 ，所以数列 是以 2 为首项，1 为公差的等差数列， ，即 ． 因为 ，所以不等式 ，等价于 ． 记 ， 时， ． 所以 时， ． 所以 ，所以整数 的最大值为 4． 考点：1．数列的通项公式；2．解不等式． 17．（1） ；（2） . 1n = 2 1 12 2S a= − 1 4a = 2n ≥ 1 2 2n n nS a− = − 12 2n n nS a += − 12 2 2n n n na a a −= − − 12 2n n na a −= + 1 1 12 2 n n n n a a − −− = 1 1 22 a = 2 n n a    12 n n a n= + ( 1) 2n na n= + ⋅ 0na > 22 3 (5 ) nn n aλ− − < − 2 35 2n nλ −− > 1 2 2 3 1 1, ,2 2 4n n nb b b −= = − = 2n ≥ 11 2 1 2 12 2 3 4 6 2 nn n n n b n nb n ++ − −= =− − 3n ≥ 1 max 3 31,( ) 8 n n n b b bb + < = = 3 3 375 , 58 8 8 λ λ− > < − = λ 3 π 3 3 4 【解析】 【分析】 （1）由题意，得 ，由正弦定理，化简 ， 进而得到 ，即可求解； （2）设 的外接圆半径为 ，求得 ，利用余弦定理求得 ， 进而利用面积公式，即可求解． 【详解】 （1）因为 是 与 的等差中项. 所以 . 由正弦定理得 ， 从而可得 ， 又 为三角形的内角，所以 ，于是 ， 又 为三角形内角，因此 . （2）设 的外接圆半径为 ，则 ， ， 由余弦定理得 ， 即 ，所以 . 所以 的面积为 . 【点睛】 在解有关三角形的题目时，要有意识地考虑用哪个定理更合适，或是两个定理都要用，要抓 住能够利用某个定理的信息．一般地，如果式子中含有角的余弦或边的二次式时，要考虑用 余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明 显时，则要考虑两个定理都有可能用到． 18．（1）0.32 ；（2）众数是 170，中位数是 168.25 ；（3） 【解析】 2 cos cos cosc A a B b A= + 2sin cos sinC A C= cos A ABC∆ R 2 sin 3a R A= = 3bc = sin 2c A π −   cosa B cosb A 2 cos cos cosc A a B b A= + 2sin cos sin cos sin cosC A A B B A= + 2sin cos sinC A C= C sin 0C ≠ 1cos 2A = A 3A π= ABC∆ R 1R = 2 sin 3a R A= = ( )22 2 2 2 cos 33a b c bc b c bc π= + − = + − 3 12 3bc= − 3bc = ABC∆ 1 3 3sin2 4S bc A= = 4 5 【分析】 （1）利用频率分布直方图能求出被采访人恰好在第 2 组或第 6 组的概率； （2）利用频率分布直方图能求出众数和中位数； （3）共 50×0.12＝6 人，其中男生 3 人，设为 a，b，c，女生三人，设为 d，e，f，利用列举 法能求出至少有 1 名女性市民的概率． 【详解】 （1）被采访人拾好在第 2 组或第 6 组的概率 . （2）众数： ； 设中位数为 ，则 ∴中位数 . （3）共 人，其中男生 3 人，设为 ， ， ，女生三人，设为 ， ， ， 则任选 2 人， 可能为 ， ， ， ， ， ， ， ， ， ， ， ， ， ， ，共 15 种， 其中两个全是男生的有 ， ， ，共 3 种情况， 设事件 ：至少有 1 名女性，则至少有 1 名女性市民的概率 . 【点睛】 本题考查概率、众数、中位数的求法，考查频率分布直方图、列举法等基础知识，考查运算 求解能力，属于基础题． 19．（1）见解析；（2） 【解析】 【分析】 （1）推导出 BC⊥PO，BC⊥DE，从而 BC⊥平面 PED，由此能证明平面 PED⊥平面 BCF； （2）取 AD 的中点 G，连结 BG，FG，从而 BG∥DE，进而 BG∥平面 PDE，平面 BGF∥平面 PDE，由此能求出四棱锥 F﹣ABED 的体积． 4 0.07 4 0.01 0.32p = × + × = 168 172 1702 + = x ( ) ( )0.05 4 0.07 4 168 0.08 0.2 0.28 168 0.08 0.5x x× + × + − × = + + − × = 0.5 0.48 168 168.250.08x −= + = 50 0.12 6× = a b c d e f { },a b { },a c { },a d { },a e { },a f { },b c { },b d { },b e { },b f { },c d { },c e { },c f { },d e { },d f { },e f { },a b { },a c { },b c A ( ) 3 41 15 5P A = − = 3 3 2 【详解】 证明： 平面 ABCD， 平面 ABCD， ， 依题意 是等边三角形，E 为棱 BC 的中点， ， 又 ，PO， 平面 PED， 平面 PED， 平面 BCF， 平面 平面 BCF． 解： Ⅱ 取 AD 的中点 G，连结 BG，FG， 底面 ABCD 是菱形，E 是棱 BC 的中点， ， 平面 PDE， 平面 PDE， 平面 PDE， 平面 PDE， ， 平面 平面 PDE， 又平面 平面 ，平面 平面 ， ， 为 PA 的中点， ， 点 F 到平面 ABED 的距离为 ， 四棱锥 的体积： ． 【点睛】 本题考查面面垂直的证明，考查四棱锥的体积的求法，考查空间中线线、线面、面面间的位 置关系，考查运算求解能力，考查函数与方程思想，是中档题． 20．（1） （2） 或 【解析】 【分析】 ( )1 PO ⊥ BC ⊂ BC PO∴ ⊥ BCD BC DE∴ ⊥ PO DE O∩ = DE ⊂ BC∴ ⊥ BC ⊂ ∴ PED ⊥ ( )  / /BG DE∴ BG ⊄ DE ⊂ / /BG∴ / /BF BF BG B∩ = ∴ / /BGF BGF ∩ PAD GF= PDE ∩ PAD PD= / /GF PD∴ F∴ 3 1 9 32 3 2 3 sin602 2 2ABEDS  四边形 = × × × × = 12 POd = = ∴ F ABED− 1 1 9 3 3 313 3 2 2F ABED ABEDV S d四边形− = ⋅ ⋅ = × × = 2 2 12 x y+ = 2 62 3t− < < − 2 6 23 t< < （1）设 ，由 在椭圆上求出 ，再由椭圆过点 得 ，从而可得 ，得椭圆方程； （2）由题意可知直线 的斜率存在，设 ， ， ， ，直线方程与椭圆方程联立，并消元后应用韦达定理得 ，同时注意 ，由弦长公式表示出 后可得 的取值范围，由向量线性运算求出 点坐标，交 代入椭圆方程得出 的关系，从而得 的范围． 【详解】 （1）设 ，因为 ，则点 关于 轴的对称点 . ， ，又由椭圆的方程得 ， 所以 ， 又椭圆 过圆 的圆心 ， 所以 ， ，所以椭圆 的标准方程为 ； （2）由题意可知直线 的斜率存在，设 ， ， ， 由 得： 由 ，得： ， . ， ( , )P x y P 2 2 2 2 2 1 2PQ RH y bk k a x a ⋅ = = =− (0,1) 2 1b = 2a AB : ( 2)AB y k x= − ( )1 1,A x y ( )2 2,B x y ( )0 0,P x y 1 2 1 2,x x x x+ > 0∆ AB k P ,t k t ( , )P x y ( ,0), ( ,0)Q a R a− P x ( , )H x y− PQ yk x a = + RH yk a x = − ( )2 2 2 2 2 2 2 21 x by b a xa a  = − = −   2 2 2 2 2 1 2PQ RH y bk k a x a ⋅ = = =− C 2 2( 1) 4x y+ − = (0,1) 2 2a = 2 1b = C 2 2 12 x y+ = AB : ( 2)AB y k x= − ( )1 1,A x y ( )2 2,B x y ( )0 0,P x y 2 2 ( 2) 12 y k x x y = − + = ( )2 2 2 21 2 8 8 2 0k x k x k+ − + − = ( )( )4 2 264 4 2 1 8 2 0k k k∆ = − + − > 2 1 (*)2k < 2 1 2 2 8 1 2 kx x k ∴ + = + 2 1 2 2 8 2 1 2 kx x k −= + 2 5| | 3AB < ( )22 2 1 2 1 2 1 2 2 51 1 4 3k x x k x x x x∴ + − = + ⋅ + − < ， ，结合（*）得： . ， . 从而 ， . ∵点 在椭圆上， ， 整理得： 即 ， ， 或 . 【点睛】 本题考查求椭圆的标准方程，考查直线与椭圆相交问题．直线与椭圆相交一般采取设而不求 思想，即设交点坐标为 ，由直线方程与椭圆方程联立方程组消元后应用韦 达定理得 ，并把这个结论代入题中其他条件中求解． 21．(1)增区间 减区间 (2) 【解析】 试题分析： 先求出函数的导数，令导函数大于 ，解出即可； （2）构造新函数 ，求导，分类讨论 的取值，在不同情 况下讨论，取得最后结果 解析：（1）由已知可得 的定义域为 ( ) ( ) 4 2 2 2 22 64 8 2 201 4 1 2 91 2 k kk kk  − ∴ + − × < ++  2 1 4k∴ > 21 1 4 2k< < OA OB tOP+ =    ( ) ( )1 2 1 2 0 0, ,x x y y t x y∴ + + = ( ) 2 1 2 0 2 8 1 2 x x kx t t k += = + ( ) ( )1 2 0 1 2 2 1 44 1 2 y y ky k x x kt t t k + −= = + − =   + P ( ) ( ) 2 2 2 2 2 8 42 2 1 2 1 2 k k t k t k    −   ∴ + = + +       ( )2 2 216 1 2k t k= + 2 2 88 1 2t k = − + 28 43 t∴ < < 2 62 3t∴− < < − 2 6 23 t< < 1 1 2 2( , ),( , )x y x y 1 2 1 2,x x x x+ 01)（ ， (1, )+∞ ( ,1).−∞ ( )1 0 ( ) ( )2 1ln 12 2 xg x x x k x= − + − − − k ( )f x ( )0, .+∞ ( ) 1 ,f x ax =′ − ( )1 1 0,f a∴ = − =′ 1.a∴ = ( ) 1 11 ,xf x x x −∴ = − =′ ( ) 0 0 1,f x x>′ < <令 得 ( ) 0 1,f x x′令 得 ( ) 01 1 + .f x∴ ∞的单调递增区间为（ ，），单调递减区间为（， ） （2）不等式 可化为 ， ， 不适合题意. 适合题意. 适合题意. 综上， 的取值范围是 点睛：含有参量的不等式题目有两种解法，一是分离含参量，二是带着参量一起计算，本题 在处理问题时含有参量运算，然后经过分类讨论，求得符合条件情况的参量范围 22．（1） ；（2） . 【解析】 【分析】 （1）先将 化为普通方程，再由 ，即可得到极坐标方程. （2）根据题意求得 A、B 两点的坐标，得到极径 ，再由 可得结果. ( ) ( )2 12 12 2 xf x x k x− + + > − ( )2 1ln 12 2 xx x k x− + − > − ( ) ( )2 1ln 1 ,( 1),2 2 xg x x x k x x= − + − − − >令 ( ) ( )2 1 11 1 ,x k xg x x kx x − + − += − + − =′令 1,x > ( ) ( )2 1 1,h x x k x= − + − +令 ( ) 1 ,2 kh x x −=的对称轴为 1 1 1,2 k k − ≤ ≥ −当 时，即 ( ) 01 ) ,h x x易知 在（， 上单调递减 ( ) ( )1 1 ,h x h k∴ < = − ( )1, 0,k h x≥ ≤若 则 ( ) 0,g x∴ ′ ≤ ( ) 01 ) ,g x x∴ 在（， 上单调递减 ( ) ( )1 0g x g∴ < = ( )-1 1, 1 0,k h≤若 则 ( )0 01 ) 0,x x x g x∴ ∈ >′必存在 使得 （， 时 ( ) 01 ) ,g x x∴ 在（， 上单调递增 ( ) ( )1 0 ,g x g∴ > = 恒成立 1 1 1,2 k k − > < −当 时，即 ( )0 01 ) ,x h x x易知必存在 使得 在（， 上单调递增 ( ) ( )1 1 0,h x h k∴ > = − > ( ) 0,g x∴ ′ > ( ) 01 ) ,g x x∴ 在（， 上单调递增 ( ) ( )1 0 ,g x g∴ > = 恒成立 k ( ),1 .−∞ 2 2 2 1 sincos 4 θθρ = + 4 7 47 + 1C cos sin x y ρ θ ρ θ =  = ,A B ρ ρ A BAB ρ ρ= − 【详解】 （1）由题意知 的直角坐标方程为 ，由 ，可得 的极坐标方程 为 ，化简整理得 . （2）由题意得直线 的极坐标方程为 ，所以 可得 ．同理 可得 ， . 【点睛】 本题考查参数方程与普通方程的互化、普通方程与极坐标方程的互化，极坐标方法求两点间 的距离，需熟记公式，考查学生化简计算的能力，属基础题． 23．（1） ； （2） . 【解析】 【分析】 （1）去掉绝对值符号，得到分段函数，然后求解不等式的解集． （2）不等式 　，根据已知条件，结合绝对值 不等式的几何意义，转化求解 即可． 【详解】 因为 ，所以 ． （1）当 时， 1C 2 2 14 yx + = cos sin x y ρ θ ρ θ =  = 1C 2 2 2 2 sincos 14 ρ θρ θ + = 2 2 2 sin 1cos 4 θθ ρ+ = l 3 πθ = 3 8cos 0 πθ ρ θ  =  + = ( 4, )3A π− 2 2 2 3 sin 1cos 4 πθ θθ ρ  =  + = 4 7( , )7 3B π 4 7 47A BAB ρ ρ= − = + 1 13x x  ≤ ≤    70, 2      ( ) ( )3 4 4 3f x t t f x t t+ − < + ⇔ ≤ + − − ( ) ( )max maxf x g t≤ 0m > ( ) 3 , 2 2 3 , 3 , x m x m f x x m x m x m m x m x m x m − ≤ − = + − − = − − < <  − + ≥ 1 2m = ( ) 3 1,2 2 1 1 13 , ,2 2 2 3 1,2 2 x x f x x x x x  − ≤ − = − − < <   − + ≥ 所以由 ，可得 或 或 ， 解得 或 ， 故原不等式的解集为 ． （2）因为 ， 令 ，则由题设可得 ， 由 ，得 ． 因为 ，所以 ． 故 ，从而 ，即 ， 又已知 ，故实数 的取值范围是 ． 【点睛】 本题考查了绝对值不等式的解法，考查了绝对值不等式的几何意义的应用；绝对值不等式问 题中的求参数范围问题，一般思路是：借助绝对值的几何意义、零点分段法等，先求出相关 函数的最值或值域，再根据题目要求求解. ( ) 1 2f x ≥ 3 1 ,2 2 1 2 x x  − ≥  ≤ − 1 13 ,2 2 1 1 2 2 x x  − ≥ − < < 3 1 2 2 1 2 x x − + ≥  ≥ 1 1 3 2x≤ < 1 12 x≤ ≤ 1 13x x  ≤ ≤    ( ) ( )3 4 4 3f x t t f x t t+ − < + ⇔ ≤ + − − ( ) 4 3g t t t= + − − ( ) ( )max maxf x g t≤ ( ) 3 , 3 , 3 , x m x m f x x m m x m x m x m − ≤ − = − − < <  − + ≥ ( ) ( )max 2f x f m m= = ( ) ( )4 3 4 3 7t t t t+ − − ≤ + − − = ( )7 7g t− ≤ ≤ ( )max 7g t = 2 7m < 7 2m < 0m > m 70, 2     