2020届二轮复习随机变量及其分布列教案（全国通用）

2020届二轮复习随机变量及其分布列教案（全国通用）

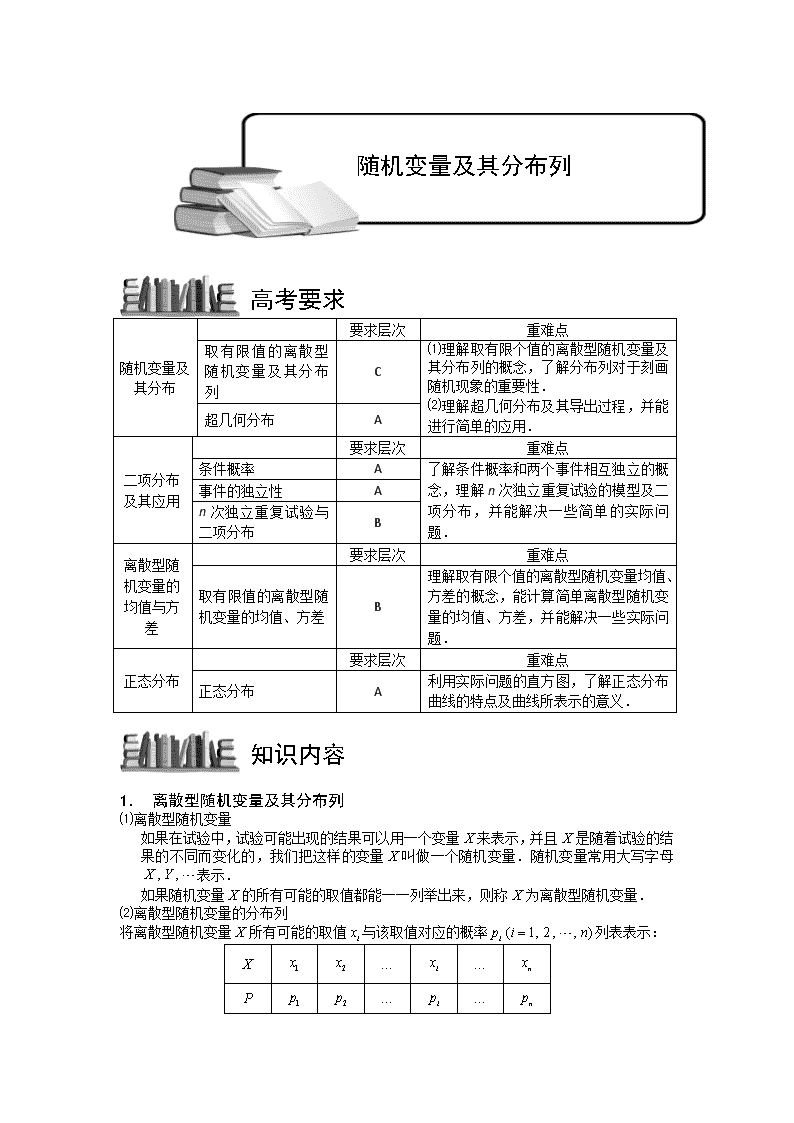
要求层次 重难点 取有限值的离散型 随机变量及其分布 列 C随机变量及 其分布 超几何分布 A ⑴理解取有限个值的离散型随机变量及 其分布列的概念，了解分布列对于刻画 随机现象的重要性． ⑵理解超几何分布及其导出过程，并能 进行简单的应用． 要求层次 重难点 条件概率 A 事件的独立性 A 二项分布 及其应用 n 次独立重复试验与 二项分布 B 了解条件概率和两个事件相互独立的概 念，理解 n 次独立重复试验的模型及二 项分布，并能解决一些简单的实际问 题． 要求层次 重难点离散型随 机变量的 均值与方 差 取有限值的离散型随 机变量的均值、方差 B 理解取有限个值的离散型随机变量均值、 方差的概念，能计算简单离散型随机变 量的均值、方差，并能解决一些实际问 题． 要求层次 重难点 正态分布 正态分布 A 利用实际问题的直方图，了解正态分布 曲线的特点及曲线所表示的意义． 1． 离散型随机变量及其分布列 ⑴离散型随机变量 如果在试验中，试验可能出现的结果可以用一个变量 来表示，并且 是随着试验的结 果的不同而变化的，我们把这样的变量 叫做一个随机变量．随机变量常用大写字母 表示． 如果随机变量 的所有可能的取值都能一一列举出来，则称 为离散型随机变量． ⑵离散型随机变量的分布列 将离散型随机变量 所有可能的取值 与该取值对应的概率 列表表示： … … … … X X X , ,X Y  X X X ix ip ( 1, 2, , )i n=  X 1x 2x ix nx P 1p 2p ip np 知识内容 高考要求 随机变量及其分布列 我们称这个表为离散型随机变量 的概率分布，或称为离散型随机变量 的分布列． 2．几类典型的随机分布 ⑴两点分布 如果随机变量 的分布列为 其中 ， ，则称离散型随机变量 服从参数为 的二点分布． 二点分布举例：某次抽查活动中，一件产品合格记为 ，不合格记为 ，已知产品的合格率 为 ，随机变量 为任意抽取一件产品得到的结果，则 的分布列满足二点分布． 两点分布又称 分布，由于只有两个可能结果的随机试验叫做伯努利试验，所以这种分 布又称为伯努利分布． ⑵超几何分布 一般地，设有总数为 件的两类物品，其中一类有 件，从所有物品中任取 件 ，这 件中所含这类物品件数 是一个离散型随机变量，它取值为 时的概率 为 ， 为 和 中较小的一个 ． 我们称离散型随机变量 的这种形式的概率分布为超几何分布，也称 服从参数为 ， ， 的超几何分布．在超几何分布中，只要知道 ， 和 ，就可以根据公式求出 取不同值时的概率 ，从而列出 的分布列． ⑶二项分布 1．独立重复试验 如果每次试验，只考虑有两个可能的结果 及 ，并且事件 发生的概率相同．在相同 的条件下，重复地做 次试验，各次试验的结果相互独立，那么一般就称它们为 次独 立重复试验． 次独立重复试验中，事件 恰好发生 次的概率为 ． 2．二项分布 若将事件 发生的次数设为 ，事件 不发生的概率为 ，那么在 次独立重复 试验中，事件 恰好发生 次的概率是 ，其中 ．于 是得到 的分布列 … … … … 由 于 表 中 的 第 二 行 恰 好 是 二 项 展 开 式 各对应项的值，所以称这样的散型随机变量 服从参数为 ， 的二项分布， 记作 ． 二项分布的均值与方差： 若离散型随机变量 服从参数为 和 的二项分布，则 ， ． ⑷正态分布 X X X X 1 0 P p q 0 1p< < 1q p= − X p 1 0 80% X X X 1 0 P 0.8 0.2 0 1− N M n ( )n N≤ n X m C C( ) C m n m M N M n N P X m − −= = (0 m l≤ ≤ l n M ) X X N M n N M n X ( )P X m= X A A A n n n A k ( ) C (1 )k k n k n nP k p p −= − ( 0, 1, 2, , )k n=  A X A 1q p= − n A k ( ) Ck k n k nP X k p q −= = 0, 1, 2, ,k n=  X X 0 1 k n P 0 0C n n p q 1 1 1C n n p q − Ck k n k n p q − 0Cn n n p q 0 0 1 1 1 0( ) C C C Cn n n k k n k n n n n n nq p p q p q p q p q− −+ = + + + +  X n p ~ ( , )X B n p X n p ( )E X np= ( )D x npq= ( 1 )q p= − 1． 概率密度曲线：样本数据的频率分布直方图，在样本容量越来越大时， 直方图上面的折线所接近的曲线．在随机变量中，如果把样本中的任一数据看作随机变 量 ，则这条曲线称为 的概率密度曲线． 曲线位于横轴的上方，它与横轴一起所围成的面积是 ，而随机变量 落在指定的两个 数 之间的概率就是对应的曲边梯形的面积． 2．正态分布 ⑴定义：如果随机现象是由一些互相独立的偶然因素所引起的，而且每一个偶然因素 在总体的变化中都只是起着均匀、微小的作用，则表示这样 的随机现象的随机变量的概率分布近似服从正态分布． 服从正态分布的随机变量叫做正态随机变量，简称正态变量． 正态变量概率密度曲线的函数表达式为 ， ，其中 ， 是参数，且 ， ． 式中的参数 和 分别为正态变量的数学期望和标准差．期望 为 、标准差为 的正态分布通常记作 ． 正态变量的概率密度函数的图象叫做正态曲线． ⑵标准正态分布：我们把数学期望为 ，标准差为 的正态分布叫做标准正态分布． ⑶重要结论： ①正态变量在区间 ， ， 内，取值的概率分 别是 ， ， ． ②正态变量在 内的取值的概率为 ，在区间 之外的取值的概率 是 ，故正态变量的取值几乎都在距 三倍标准差之内，这就是正态分布的 原则． ⑷若 ， 为其概率密度函数，则称 为概率分布 函数，特别的， ，称 为标准正态分布函数． ． 标准正态分布的值可以通过标准正态分布表查得． 分布函数新课标不作要求，适当了解以加深对密度曲线的理解即可． 3．离散型随机变量的期望与方差 1．离散型随机变量的数学期望 定义：一般地，设一个离散型随机变量 所有可能的取的值是 ， ，…， ，这些 值对应的概率是 ， ，…， ，则 ，叫做这个离散型随 机变量 的均值或数学期望（简称期望）． 离散型随机变量的数学期望刻画了这个离散型随机变量的平均取值水平． 2．离散型随机变量的方差 一般地，设一个离散型随机变量 所有可能取的值是 ， ，…， ，这些值对应的 概率是 ， ，…， ，则 叫 做这个离散型随机变量 的方差． 离散型随机变量的方差反映了离散随机变量的取值相对于期望的平均波动的大小（离散 程度）． 的算术平方根 叫做离散型随机变量 的标准差，它也是一个衡量离散型随 X X 1 X a b， 2 2 ( ) 21( ) 2π x f x e µ σ σ −− = ⋅ x∈R µ σ 0σ > µ−∞ < < +∞ µ σ µ σ 2( , )N µ σ 0 1 ( , )µ σ µ σ− + ( 2 , 2 )µ σ µ σ− + ( 3 , 3 )µ σ µ σ− + 68.3% 95.4% 99.7% ( )−∞ + ∞， 1 ( 3 3 )µ σ µ σ− +， 0.3% x µ= 3σ 2~ ( )Nξ µ σ， ( )f x ( ) ( ) ( )x F x P x f t dtξ −∞ = = ∫≤ 2~ (0 1 )N ξ µ σ − ， 2 21( ) 2 tx x e dtφ − −∞ = ∫ π ( ) ( )xP x µξ φ σ −< = X 1x 2x nx 1p 2p np 1 1 2 2( ) n nE x x p x p x p= + + + X X 1x 2x nx 1p 2p np 2 2 2 1 1 2 2( ) ( ( )) ( ( )) ( ( ))n nD X x E x p x E x p x E x p= − + − + + − X ( )D X ( )D x X 机变量波动大小的量． 3． 为随机变量， 为常数，则 ； 4． 典型分布的期望与方差： ⑴二点分布：在一次二点分布试验中，离散型随机变量 的期望取值为 ，在 次二 点分布试验中，离散型随机变量 的期望取值为 ． ⑵二项分布：若离散型随机变量 服从参数为 和 的二项分布，则 ， ． ⑶超几何分布：若离散型随机变量 服从参数为 的超几何分布， 则 ， ． 4．事件的独立性 如果事件 是否发生对事件 发生的概率没有影响，即 ， 这时，我们称两个事件 ， 相互独立，并把这两个事件叫做相互独立事件． 如果事件 ， ，…， 相互独立，那么这 个事件都发生的概率，等于每个事件发 生的概率的积，即 ，并且上式中任意多个事 件 换成其对立事件后等式仍成立． 5．条件概率 对于任何两个事件 和 ，在已知事件 发生的条件下，事件 发生的概率叫做条件概 率，用符号“ ”来表示．把由事件 与 的交（或积），记做 （或 ）． 版块一：离散型随机变量及其分布列 【例1】 以下随机变量中，不是离散型随机变量的是： ⑴ 某城市一天之内发生的火警次数 ； ⑵ 某城市一天之内的温度 ． 【考点】离散型随机变量的定义 【难度】1 星 【题型】解答 【关键词】无 【解析】略 【答案】⑴ 是随机变量，其取值为 ； ⑵ 不是随机变量，它可以取某一范围内的所有实数，无法一一列举． 【例2】 抛掷两颗骰子，所得点数之和为 ，那么 表示的随机试验结果是（ ） A．一颗是 3 点，一颗是 1 点 B．两颗都是 2 点 C．两颗都是 4 点 D．一颗是 3 点，一颗是 1 点或两颗都是 2 点 【考点】离散型随机变量的定义 X a b， 2( ) ( ) ( ) ( )E aX b aE X b D aX b a D X+ = + + =， X p n X np X n p ( )E X np= ( )D x npq= ( 1 )q p= − X N M n， ， ( ) nME X N = 2 ( )( )( ) ( 1) n N n N M MD X N N − −= − A B ( | ) ( )P B A P B= A B 1A 2A nA n 1 2 1 2( ) ( ) ( ) ( )n nP A A A P A P A P A= × × ×   iA A B A B ( | )P B A A B D A B=  D AB= X Y X 0 1 2 ，， ， Y ξ 4ξ = 典例分析 【难度】1 星 【题型】选择 【关键词】无 【解析】对 A，B 中表示的随机试验的结果，随机变量均取值 4， 而 D 是 代表的所有试验结果．掌握随机变量的取值与它刻画的随机试验 的结果的对应关系是理解随机变量概念的关键． 【答案】D； 【例3】 如果 是一个离散型随机变量，则假命题是（ ） A． 取每一个可能值的概率都是非负数； B． 取所有可能值的概率之和为 1； C． 取某几个值的概率等于分别取其中每个值的概率之和； D． 在某一范围内取值的概率大于它取这个范围内各个值的概率之和 【考点】离散型随机分布列的性质 【难度】1 星 【题型】选择 【关键词】无 【解析】略 【答案】D； 【例4】 有六节电池，其中有 2 只没电，4 只有电，每次随机抽取一个测试，不放回， 直至分清楚有电没电为止，所要测试的次数 为随机变量，求 的分布列． 【考点】离散型随机分布列的性质 【难度】3 星 【题型】解答 【关键词】无 【解析】略 【答案】容易知道 ． ∵ 表示前 2 只测试均为次品，∴ ∵ 表示前两次中一好一坏，第三次为坏，∴ ∵ 表示前四只均为好，或前三只中一坏二好，第四个为坏， ∴ ∵ 表示前四只三好一坏，第五只为坏或前四只三好一坏第五只为好 ∴ ∴ 分布列为 4ξ = ξ ξ ξ ξ ξ ξ ξ 2, 3, 4, 5ξ = 2ξ = 2 2 2 6 A 1( 2) A 15P ξ = = = 3ξ = 1 1 2 2 4 2 3 6 2( 3) 15 C C AP A ξ = = = 4ξ = 1 2 34 2 4 34 4 4 6 6 1 1 4( 4) 15 5 15 C C AAP A A ξ = = + = + = 5ξ = 1 3 4 1 3 4 2 4 4 2 4 4 5 5 6 6 8( 5) 15 C C A C C AP A A ξ = = + = 2 3 4 5 【例5】 设随机变量 所有可能取值为 ，且已知概率 与 成正比，求 的分布． 【考点】离散型随机分布列的性质 【难度】2 星 【题型】解答 【关键词】无 【解析】略 【 答 案 】 （ 为 常 数 ），由 分 布 列 的 性 质 有 ， 解 得 ． 因此 的分布为 ． 【例6】 一批产品分为一、二、三级，其中一级品是二级品的两倍，三级品为二级品的 一 半 ， 从 这 批 产 品 中 随 机 抽 取 一 个 检 验 ， 其 级 别 为 随 机 变 量 ， 则 （ ） A． B． C． D． 【考点】离散型随机分布列的性质 【难度】3 星 【题型】选择 【关键词】无 【解析】设二级品有 个，一级品有 个，三级品有 个，总数为 个． ∴ 分布列为 【答案】D； 【例7】 随 机 变 量 的 分 布 列 ， 为 常 数 ， 则 （ ） ξ P 1 15 2 15 4 15 8 15 ξ 1 2 3 4， ， ， ( )P kξ = k ξ ( )P k akξ = = a 2 3 4 1a a a a+ + + = 1 10a = ξ ( ) 10 kP kξ = = ξ 1 5 3 3P ξ  =  ≤ ≤ 1 7 2 7 3 7 4 7 k 2k 2 k 7 2 k 1 5 4( ) ( 1)3 3 7P Pξ ξ= = =≤ ≤ X ( ) ( 1 2 3 4)( 1) pP X k kk k = = =+ ， ， ， p 1 5 2 2P X < < =   A． B． C． D． 【考点】离散型随机分布列的性质 【难度】3 星 【题型】选择 【关键词】无 【解析】 的分布列为 ， ∴ ． ． 【答案】D； 【例8】 在第 路公共汽车都要依靠的一个站（假设这个站只能停靠一辆汽 车），有一位乘客等候第 路或第 路汽车．假定当时各路汽车首先到站的可 能 性 都 是 相 等 ， 则 首 先 到 站 正 好 是 这 位 乘 客 所 需 求 的 汽 车 的 概 率 等 于 ． 【考点】离散型随机分布列的计算 【难度】1 星 【题型】填空 【关键词】无 【解析】略 【答案】 ； 【例9】 （2018 广东高考） 已知随机量 服从正态分布 ，且 ，则 （ ） A． B． C． D． 【考点】离散型随机分布列的计算 【难度】2 星 【题型】选择 【关键词】2018 年，广东高考 【解析】当 时，有 ，即 ， 2 3 3 4 4 5 5 6 X 1 1 1 1 1 1 11 11 2 2 3 3 4 4 5 2 2 3 3 4 4 5 p p p p p         + + + = − + − + − + − =        × × × ×          5 4p = ( )1 5 5 1 1 51 ( 2)2 2 4 1 2 2 3 6P X P X P X   < < = = + = = × + =   × ×    1 3 6 8 16， ， ， ， 6 16 2 5 X ( )3 1N ， ( )2 4 0.6826P X =≤ ≤ ( )4P X > = 0.1588 0.1587 0.1586 0.1585 ( )3, 1X N ( )3 0, 11 X N −  ( )3 0.6826P X − =- 1≤ ≤1 X 1 2 3 4 P 1 2 p × 2 3 p × 3 4 p × 4 5 p × ， 于是 【答案】B； 【例10】袋中装有黑球和白球共 个，从中任取 个球都是白球的概率为 ，现有甲、 乙两人从袋中轮流摸取 球，甲先取，乙后取，然后甲再取……取后不放回， 直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能 的，用 表示取球终止所需要的取球次数． ⑴ 求袋中所有的白球的个数； ⑵ 求随机变量 的概率分布； ⑶ 求甲取到白球的概率． 【考点】离散型随机分布列的计算 【难度】3 星 【题型】解答 【关键词】无 【解析】略 【答案】⑴ 设袋中原有 个白球，由题意知 ， 可得 或 （舍去）即袋中原有 个白球． ⑵ 由题意， 的可能取值为 ， ， ， ， ， ． 所以 的分布列为： ⑶ 因为甲先取，所以甲只有可能在第一次，第三次和第 次取球，记“甲取到白球” 为事件 ， 则 ． 【例11】某种电子玩具按下按钮后，会出现红球或绿球，已知按钮第一次按下后，出现 红球与绿球的概率都是 ，从按钮第二次按下起，若前次出现红球，则下一次 出现红球、绿球的概率分别为 ；若前次出现绿球，则下一次出现红球、绿 球的概率分别为 ；记 第 次按下按钮后出现红球的概率为 ． ⑴求 的值； ( ) 1< 3 0.6826 0.34132P X − = ⋅ =0 ≤1 ( ) ( )4 3 1 0.5 0.3413 0.1587P X P X> = − > = − = 7 2 1 7 1 X X n 2 2 7 ( 1) C1 ( 1)2 7 67 C 7 6 2 n n n n n − −= = =× × 3n = 2n = − 3 X 1 2 3 4 5， ， ， ， 3( 1) 7P X = = ( ) 4 3 22 7 6 7P X ×= = =× 4 3 3 6( 3) 7 6 5 35P X × ×= = =× × 4 3 2 3 3( 4) 7 6 5 4 35P X × × ×= = =× × × 4 3 2 1 3 1( 5) 7 6 5 4 3 35P X × × × ×= = =× × × × X X 1 2 3 4 5 P 3 7 2 7 6 35 3 35 1 35 5 A ( ) ( ) ( ) 22( ) 1 3 5 35P A P X P X P X= = + = + = = 1 2 1 2 3 3 ， 3 2 5 5 ， ( *)n n∈N nP 2P ⑵当 时，求用 表示 的表达式； ⑶求 关于 的表达式． 【考点】离散型随机分布列的计算 【难度】5 星 【题型】解答 【关键词】无 【解析】略 【答案】⑴ 是“第二次按下按钮后出现红球”． 若第一次，第二次均出现红球，则概率为： 第一次出现绿球，第二次出现红球的概率为： ． 故所求概率为： ． ⑵第 次按下按钮出现红球的概率为： ，则出现绿球的概率为： 若第 次，第 次均出现红球，其概率为： ． 若第 次，第 次依次出现绿球，红球，其概率为： ． 于是 ； ⑶由⑵ ， 引入代定参数 ，使得 ． 上式即为 ，与 的表达式对比 ，因此 ． 于是 ． ． 版块二：几类典型的随机分布 1． 超几何分布 【例12】一盒子内装有 个乒乓球，其中 个旧的， 个新的，从中任意取 个，则取 到新球的个数的期望值是 ． 【考点】超几何分布 【难度】2 星 【题型】填空 【关键字】无 【解析】超几何分布， ． 【答案】 ； 【例13】以随机方式自 5 男 3 女的小群体中选出 5 人组成一个委员会，求该委员会中女 2n n∈N， ≥ 1nP − nP nP n 2P 1 1 1 2 3 6 ⋅ = 1 3 3 2 5 10 ⋅ = 2 1 3 7 6 10 15P = + = 1n − 1( 2)nP n− ≥ 11 nP −− 1n − n 1 1 3 nP − 1n − n 1 3(1 ) 5nP −− ⋅ 1 1 1 1 3 4 3(1 )3 5 15 5n n n nP P P P− − −= + − ⋅ = − + 1 1 1 1 3 4 3(1 )3 5 15 5n n n nP P P P− − −= + − ⋅ = − + x 1 4 ( )15n nP x P x−+ = − + 1 4 19 15 15n nP P x−= − − nP 19 3 15 5x− = 9 19x = − 1 1 1 1 9 4 9 4 9 4 1( ) ( ) ( ) ( )19 15 19 15 19 15 38 n n n nP P P− − −− = − − = = − − = − ⋅ 14 1 9( ) ( 2)15 38 19 n nP n n−= − ⋅ + ∈N， ≥ 10 3 7 4 4 7 2.810 × = 2.8 性委员人数的概率分布、期望值与方差． 【考点】超几何分布 【难度】3 星 【题型】解答 【关键字】无 【解析】设女性委员的人数为 ，则 服从参数为 的超几何分布，其概率分布 为 ， 期望 ，方差 ． 【答案】概率分布： ， 期望： ，方差： ． 【例14】在 个同类型的零件中有 2 个次品，抽取 3 次进行检验，每次任取一个，并且 取出不再放回，若以 和 分别表示取出次品和正品的个数．求 的期望值 及方差． 【考点】超几何分布 【难度】3 星 【题型】解答 【关键字】无 【解析】抽取样本连续抽取 3 次，也可认为一次抽取 3 个，所以 服从参数为 的 超几何分布． 服从参数为 的超几何分布．且 ． 于是 ， ． 【答案】 ， ． 【例15】某人可从一个内有 2 张 元，3 张 元的袋子里任取 2 张，求他获得钱数的 期望值． 【考点】超几何分布 【难度】3 星 【题型】解答 【关键字】无 【解析】方法一：设他取得 元的张数为 ，则 服从参数为 的超几何分 布． ． 时他所获得的钱数分别为 ． 因此他获得钱数的期望值为： 元． X X (8 3 5)， ， 1 15 30 10( 0) ( 1) ( 2) ( 3)56 56 56 56P X P X P X P X= = = = = = = =， ， ， 3 5 15( ) 8 8E X ×= = 2 5 (8 5) (8 3) 3 225( ) 0.50228 (8 1) 448D X × − × − ×= = ≈× − 1 15 30 10( 0) ( 1) ( 2) ( 3)56 56 56 56P X P X P X P X= = = = = = = =， ， ， 15 8 0.5022 12 ξ η ξ η， ξ 12 2 3， ， η 12 10 3， ， 3ξ η+ = 2 2 3 1 5 3(12 3) 2(12 2) 15312 2 2 12 (12 1) 44E E E Dξ η ξ ξ× − × −= = = − = = =−， ， 2 15( 1) 44D Dη ξ= − = 1 5 15 2 2 44E E Dξ η ξ= = =， ， 15 44Dη = 100 50 100 X X 5 2 2， ， 0 2 1 1 2 0 2 3 2 3 2 3 2 2 2 5 5 5 C C C C C C3 6 1( 0) ( 1) ( 2)C 10 C 10 C 10P X P X P X= = = = = = = = =， ， 0 1 2X = ，， 100 150 200， ， 100 ( 0) 150 ( 1) 200 ( 2) 140P X P X P X= + = + = = 方法二：设他取得 元的张数为 ，则 服从参数为 的超几何分布． 由公式知 ． 因此他获得钱数的期望值为： 元． 【答案】 ． 【例16】某人有一张 元与 张 元，他从中随机地取出 张给孙儿、孙女，每人一 张，求孙儿获得钱数的期望值． 【考点】超几何分布 【难度】3 星 【题型】解答 【关键字】无 【解析】方法一：设他取出 元的张数为 ，则 服从参数为 的超几何分 布． ． 时他所取出的钱数分别为 ． 因此他取出钱数的期望值为： ． 孙儿获得钱数的期望值为 ． 方法二：设他取得 元的张数为 ，则 服从参数为 的超几何分布． 由公式知 ． 因此他取出钱数的期望值为： 元． 【答案】 ． 【例17】甲、乙两人参加一次英语口语考试，已知在备选的 10 道题中，甲能答对其中 的 6 题，乙能答对其中的 8 题．规定每次考试都从备选题中随机抽出 3 题进行 测试，至少答对 2 题才算合格． ⑴ 求甲答对试题数 的分布列、数学期望与方差； ⑵ 求甲、乙两人至少有一人考试合格的概率． 【考点】超几何分布 【难度】3 星 【题型】解答 【关键字】无 【解析】⑴ 依题意， 可能取的值为 ， ． 甲答对试题数 的分布列如下： 甲答对试题数 的数学期望 ． 100 X X 5 2 2， ， 2 2 4 5 5EX ×= = 4 4100 50 (2 ) 1405 5 × + × − = 140 100 4 10 2 100 X X 5 1 2，， 0 2 1 1 1 4 1 4 2 2 5 5 C C C C6 4( 0) ( 1)C 10 C 10P X P X= = = = = =， 0 1X = ， 20 110， 20 ( 0) 110 ( 1) 12 44 56P X P X= + = = + = 1 56 282 ⋅ = 100 X X 5 1 2，， 1 2 2 5 5EX ×= = 2 2100 10 (2 ) 565 5 × + × − = 56 X X 0 1 2 3，， ， 3 6 4 3 10 C C( ) 0 1 2 3C k k P X k k −⋅= = =， ， ， ， X X 0 1 2 3 P 1 30 3 10 1 2 1 6 X 1 3 1 1 9( ) 0 1 2 330 10 2 6 5E X = × + × + × + × = ； （注： 服从参数为 的超几何分布，故由公式得 ） ⑵ 设甲、乙两人考试合格的事件分别为 、 ， 则 ， ． 因为事件 、 相互独立， 法一： ∴ 甲 、 乙 两 人 考 试 均 不 合 格 的 概 率 为 ． ∴甲、乙两人至少有一人考试合格的概率为 ． 法二： ∴甲、乙两人至少有一个考试合格的概率为 ． 【答案】⑴ 甲答对试题数 的分布列如下： ． ；⑵ ． 2． 二项分布 【例18】已知随机变量 服从二项分布， ，则 等于 ． 【考点】二项分布 【难度】1 星 【题型】填空 【关键字】无 【解析】 【答案】 ； 【例19】某人参加一次考试， 道题中解对 道则为及格，已知他的解题正确率为 ， 则他能及格的概率为_________（保留到小数点后两位小数） 【考点】二项分布 【难度】2 星 【题型】填空 【关键字】无 【 解 析 】 他 能 及 格 则 要 解 对 道 题 中 解 对 道 或 道 ： 解 对 道 的 概 率 为 2 2 2 29 1 9 3 9 1 9 1( ) 0 1 2 35 30 5 10 5 2 5 6D X        = − × + − × + − × + − ×               14 25 = X 10 6 3， ， 3 6 9( ) 10 5E X ×= = A B 1 1 2( ) 2 6 3P A = + = 2 1 3 8 2 8 3 10 C C C 56 56 14( ) C 120 15P B + += = = A B 2 14 1( ) ( ) ( ) 1 13 15 45P A B P A P B   ⋅ = = − − =     1 441 ( ) 1 45 45P P A B= − ⋅ = − = ( ) ( ) ( )P P A B P A B P A B= ⋅ + ⋅ + ⋅ ( ) ( ) ( ) ( ) ( ) ( )P A P B P A P B P A P B= + + 2 1 1 14 2 14 44 3 15 3 15 3 15 45 = × + × + × = X X 0 1 2 3 P 1 30 3 10 1 2 1 6 9( ) 5E X = ( )D X = 14 25 44 45 ξ 1~ (4 )3Bξ ， ( 2)P ξ = 2 2 2 4 1 1 8C ( ) (1 )3 3 27 − = 8 27 4 3 0.4 4 3 4 3 ，解对 道的概率为 ，且 与 互斥， 他能及格的概率为 ． 【答案】 ； 【例20】从一批由 9 件正品，3 件次品组成的产品中，有放回地抽取 5 次，每次抽一件， 求恰好抽到两次次品的概率（结果保留 位有效数字）． 【考点】二项分布 【难度】2 星 【题型】解答 【关键字】无 【解析】略 【答案】有放回地抽取 5 件，视为 5 重 Bernoulli 实验． 设 A 表示“一次实验中抽到次品”， ．记 为抽到的次品数，则 ，于是 ． 【例21】某厂生产电子元件，其产品的次品率为 ，现从一批产品中的任意连续取出 2 件，求次品数 的概率分布列及至少有一件次品的概率． 【考点】二项分布 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】 的取值分别为 0、1、2 =0 表示抽取两件均为正品， ． =1 表示抽取一件正品一件次品， ． =2 表示抽取两件均为次品， ． ∴ 的概率分布列为： 0 1 2 ． 【例22】某万国家具城进行促销活动，促销方案是：顾客每消费 元，便可获得奖券 一张，每张奖券中奖的概率为 ，若中奖，则家具城返还顾客现金 元．某 顾客消费了 元，得到 3 张奖券． 3 3 4( ) C 0.4 0.6P A = ⋅ ⋅ 4 4 4 4( ) C 0.4P B = A B 3 3 4 4 4 4( ) C 0.4 0.6 C 0.4 0.18P A B+ = ⋅ ⋅ + ⋅ ≈ 0.18 2 3 1( ) 12 4P A = = X 1~ (5 )4X B ， 2 2 3 5 1 1( 2) C ( ) (1 ) 0.264 4P X = = − = 5% ξ ξ ξ 0 2 2( 0) C (1 0.05) 0.9025P ξ = = − = ξ 1 2( 1) C (1 0.05) 0.05 0.095P ξ = = − ⋅ = ξ 2 2 2( 2) C (0.05) 0.0025P ξ = = = ξ ξ P 0.9025 0.095 0.0025 ( 1) 0.095 0.0025 0.0975P ξ = + =≥ 1000 1 5 200 3400 ⑴求家具城恰好返还该顾客现金 元的概率； ⑵求家具城至少返还该顾客现金 元的概率． 【考点】二项分布 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴家具城恰好返还给该顾客现金 元，即该顾客的三张奖券有且只有一张中 奖．所求概率为 ． ⑵设家具城至少返还给该顾客现金 元为事件 ，这位顾客的三张奖券有且 只有一张中奖为事件 ，这位顾客有且只有两张中奖为事件 ，这位顾客有且 只有三张中奖为事件 ，则 ，且 是互斥事件． ． 也可以用间接法求： ． 【例23】（05 浙江） 袋子 和 中装有若干个均匀的红球和白球，从 中摸出一个红球的概率是 ， 从 中摸出一个红球的概率为 ． ⑴从 A 中有放回地摸球，每次摸出一个，有 3 次摸到红球即停止． ①求恰好摸 5 次停止的概率； ②记 5 次之内（含 5 次）摸到红球的次数为 ，求随机变量 的分布． ⑵若 两个袋子中的球数之比为 ，将 中的球装在一起后，从中摸出一 个红球的概率是 ，求 的值． 【考点】二项分布 【难度】4 星 【题型】解答 【关键字】2018 年，浙江高考 【解析】略 【答案】⑴恰好摸 5 次停止，则第 5 次摸到的是红球，前面 4 次独立重复试验摸到两次 红球，所求概率为： 随 机 变 量 的 取 值 为 ． 由 次 独 立 重 复 试 验 概 率 公 式 ，得 ， ， 200 200 200 1 2 3 1 4 48C ( ) ( )5 5 125p = ⋅ = 200 A 1A 2A 3A 1 2 3A A A A= + + 1 2 3A A A， ， 1 2 3( ) ( ) ( ) ( )P A P A P A P A= + + 1 2 2 2 3 3 3 3 3 1 4 1 4 1C ( ) ( ) C ( ) ( ) C ( )5 5 5 5 5 = ⋅ + ⋅ + 48 12 1 125 125 125 = + + 61 125 = 34 61( ) 1 ( ) 1 ( )5 125P A P A= − = − = A B A 1 3 B p ξ ξ A B， 1: 2 A B， 2 5 p 2 2 2 4 1 2 1 8C ( ) ( )3 3 3 81 × = ξ 0 1 2 3，， ， n ( ) C (1 )k k n k n nP k p p −= − 0 5 5 1 32( 0) C (1 )3 243P ξ = = × − = 1 4 5 1 1 80( 1) C (1 )3 3 243P ξ = = × × − = ， ． ⑵设袋子 中有 个球，则袋子 中有 个球，且 中红球数为 ， 中红 球数为 ，由 ，解得 ． 【例24】假设飞机的每一台发动机在飞行中的故障率都是 ，且各发动机互不影 响．如果至少 的发动机能正常运行，飞机就可以顺利地飞行．问对于多大 的 而言，四发动机飞机比二发动机飞机更安全？ 【考点】二项分布 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】分析： 台发动机中要有 台（或 、 台）正常运行，而这 台可以是任意 的．故属 次独立重复试验问题． 台发动机的情形同理．建立不等式求解． 解：四发动机飞机成功飞行的概率为 二发动机飞机成功飞行的概率为 要 使 四 发 动 机 飞 机 比 二 发 动 机 飞 机 安 全 ， 只 要 ，解得 ． 答：当发动机不出故障的概率大于 时，四发动机飞机比二发动机飞机安 全． 注：计算飞机成功飞行的概率时可从反面考虑：四发动机为 ，二发动机为 ，这样更简 单． 【例25】已知 ，求 与 ． 【考点】二项分布 【难度】1 星 【题型】解答 【关键字】无 【解析】略 【答案】由二项分布的期望与方差公式得 ． 【例26】已知随机变量 服从参数为 的二项分布，则它的期望 ， 2 2 3 5 1 1 80( 2) C ( ) (1 )3 3 243P ξ = = × × − = 32 80 2 17( 3) 1 243 81P ξ + ×= = − = A m B 2m A 1 3 m B 2mp 1 2 23 3 5 m mp m + = 13 30p = 1 P− 50% P 4 2 3 4 2 n 2 2 2 2 3 3 1 4 4 4 4 4C (1 ) C (1 ) CP P P P P⋅ ⋅ − + ⋅ ⋅ − + ⋅ 2 2 3 46 (1 ) 4 (1 )P P P P P= − + − + 1 2 2 2 2 2C (1 ) C 2 (1 )P P P P P P⋅ ⋅ − + = − + 2 2 3 4 26 (1 ) 4 (1 ) 2 (1 )P P P P P P P P− + − + > − + 2( 1) (3 2) 0P P P⇒ − − > 2 13 P< < 2 3 0 0 4 1 1 3 4 41 C (1 ) C (1 )P P P P− ⋅ ⋅ − − ⋅ ⋅ − 0 0 2 21 C (1 )P P− ⋅ ⋅ − (10 0.8)X B ，~ ( )E X ( )D X ( ) 8 ( ) (1 ) 1.6E X np D X np p= = = − =， X 6 0.4， ( )E X = 方差 ． 【考点】二项分布 【难度】2 星 【题型】填空 【关键字】无 【解析】略 【答案】 ． 【例27】同时抛掷 枚均匀硬币 次，设 枚硬币正好出现 枚正面向上， 枚反面向上 的次数为 ，则 的数学期望是（ ） A． B． C． D． 【考点】二项分布 【难度】3 星 【题型】选择 【关键字】无 【解析】抛掷一次， 枚硬币正好出现 枚正面向上， 枚反面向上的概率是 ，故 ，因此数学期望为 ，选 C． 【答案】C； 【例28】某班级有 人，设一年 天中，恰有班上的 （ ）个人过生日的天数 为 ，求 的期望值以及至少有两人过生日的天数的期望值． 【考点】二项分布 【难度】5 星 【题型】解答 【关键字】无 【解析】略 【答案】 个人在哪天过生日可看成 次独立重复试验，设某天过生日的人数为 ，则 ，因此 ， 天 每 天 有 多 少 人 过 生 日 ， 又 可 看 作 次 独 立 重 复 试 验 ， 因 此 ． 由二项分布的期望值公式知： ． 没有人过生日的天数期望值为 ． 恰有一人过生日的天数期望值为 ． 因此至少有两人过生日的天数的期望值为： ． ( )D X = 2.4 1.44， 4 80 4 2 2 ξ ξ 20 25 30 40 4 2 2 2 4 4 C 3 2 8 = 3~ (80 )8Bξ ， 380 308 × = n 365 m m n≤ X X n n Y 1~ ( )365Y B n， 1 364 364( ) C ( ) ( ) C365 365 365 n m m m n m m n n nP Y m − −= = = 365 365 ~ (365 ( ))X B P Y m=， 1 364( ) 365 ( ) C 365 n m m n nE X P Y m − −= ⋅ = = 0 1 1 364 364C 365 365 n n n n n− −= 1 1 1 1 1 364 364C 365 365 n n n n nn − − − −= 1 1 1 364 364365 365 365 n n n nn − − −− − ⋅ 【例29】将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下 落．小球在下落的过程中，将 次遇到黑色障碍物，最后落入 袋或 袋中．已 知小球每次遇到黑色障碍物时，向左、右两边下落的概 率都是 ． ⑴ 求小球落入 袋中的概率 ； ⑵ 在容器入口处依次放入 个小球，记 为落入 袋中 的小球个数，试求 的概率和 的数学期望． 【考点】二项分布 【难度】4 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴ 记“小球落入 袋中”为事件 ，“小球落入 袋中”为事件 ， 则事件 的对立事件为 ，而小球落入 袋中当且仅当小球一直向左落下 或一直向右落下，故 ， 从而 ； ⑵ 显 然 ， 随 机 变 量 ， 故 ， ． 3． 正态分布 【例30】下列函数是正态分布密度函数的是（ ） A． B． C． D． 【考点】正态分布 【难度】2 星 【题型】选择 【关键字】无 【解析】略． 【答案】B； 【例31】对于标准正态分布 的概率密度函数 ，下列说法不正确的 是（ ） A． 为偶函数 3 A B 1 2 A ( )P A 4 ξ A 3ξ = ξ A A B B A B B 3 31 1 1( ) 2 2 4P B    = + =       1 3( ) 1 ( ) 1 4 4P A P B= − = − = 3~ 4 4Bξ     ， 3 3 4 3 1 27( 3) C 4 4 64P ξ  = = × × =   34 34Eξ = × = 2( ) 21( ) 2 x r f x e σ σ − = π 2 22π( ) 2π x f x e −= 2( 1) 41( ) 2 2 x f x e − = π 2 21( ) 2 x f x e= π ( )0 1N ， ( ) 2 21 2π x f x e −= ( )f x B． 最大值为 C． 在 时是单调减函数，在 时是单调增函数 D． 关于 对称 【考点】正态分布 【难度】2 星 【题型】选择 【关键字】无 【解析】 关于 对称． 【答案】D； 【例32】设 ，且总体密度曲线的函数表达式为： ， ． ⑴求 ；⑵求 及 的值． 【考点】正态分布 【难度】3 星 【题型】解答 【关键字】无 【解析】⑴ ，因此 ． ⑵ ， 由 正 态 变 量 在 区 间 内 取 值 的 概 率 是 知 ： ． ， 由对称性知 ， 所 以 ， 于是 ． 【答案】⑴ ． ⑵ ， ． 【例33】某市组织一次高三调研考试，考试后统计的数学成绩服从正态分布，其密度函 数为 ，则下列命题中不正确的是（ ） A．该市这次考试的数学平均成绩为 分 B．分数在 120 分以上的人数与分数在 分以下的人数相同 C．分数在 110 分以上的人数与分数在 分以下的人数相同 D．该市这次考试的数学标准差为 【考点】正态分布 ( )f x 1 2π ( )f x 0x > 0x ≤ ( )f x 1x = ( )f x 0x = 2~ ( )X N µ σ， 2 2 1 41( ) e 2 π x x f x − +−= x∈R µ σ， (| 1| 2)P x − < (1 2 1 2 2)P x− < < + 22 2 ( 1)2 1 2( 2)41 1( ) e e 2 π 2π 2 xx x f x −− + −−= = ⋅ 1 2µ σ= =， (| 1| 2) (1 2 1 2)P x P x− < = − < < + ( , )µ σ µ σ− + 68.3% (| 1| 2) 0.683P x − < = (1 2 1 2 2) (1 2 1 2) (1 2 1 2 2)P x P x P x− < < + = − < < + + + < +≤ 0.683 (1 2 1 2 2)P x= + + < +≤ (1 2 1 2 2) (1 2 2 1 2)P x P x+ < + = − < −≤ ≤ 1(1 2 1 2 2) [ (1 2 2 1 2 2) (1 2 1 2)]2P x P x P x+ < + = − < < + − − < < +≤ 1 (0.954 0.683) 0.13552 = − = (1 2 1 2 2) 0.683 0.1355 0.8185P x− < < + = + = 1 2µ σ= =， (1 2 1 2 2)P x+ < +≤ 0.1355= (1 2 1 2 2) 0.8185P x− < < + = 2( 80) 2001( ) 10 2 x f x eπ −−= 80 60 50 10 【难度】2 星 【题型】选择 【关键字】无 【解析】不难知道 ，由正态分布曲线的特点知答案为 B． 【答案】B； 【例34】设随机变量 服从正态分布 ， ，则下列结论正确的个数是 ． ⑴ ⑵ ⑶ ⑷ 【考点】正态分布 【难度】3 星 【题型】填空 【关键字】无 【解析】⑴⑵⑷正确． 【答案】 ； 【例35】正态变量 ， 为常数， ，若 ， 求 的值． 【考点】正态分布 【难度】3 星 【题型】解答 【关键字】无 【解析】因为 和 的区间长度相等，要使 成立， 只能是 和 关于 对称．因此 ，即 ． 于是 ． 【答案】 ； 【例36】（06 湖北） 在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布 ．已知成绩在 分以上（含 分）的学生有 名． ⑴试问此次参赛学生总数约为多少人？ ⑵若该校计划奖励竞赛成绩排在前 名的学生，试问设奖的分数线约为多少分？ 附：标准正态分布表 ． 【考点】正态分布 【难度】3 星 【题型】解答 【关键字】2018 年，湖北高考 【解析】⑴设参赛学生的分数为 ，因为 ，所以 80 10µ σ= =， ξ (0 1)N ， 0a > ____ (| | ) (| | ) (| | )P a P a P aξ ξ ξ< = < + = (| | ) 2 ( ) 1P a P aξ ξ< = < − (| | ) 1 2 ( )P a P aξ ξ< = − < (| | ) 1 (| | )P a P aξ ξ< = − > 3 2~ (1 )X N σ， c 0c > ( 2 ) (2 3 ) 0.4P c X c P c X c< < = < < = ( 0.5)P X ≤ ( 2 )c c， (2 3 )c c， ( 2 ) (2 3 )P c X c P c X c< < = < < ( 2 )c c， (2 3 )c c， 1x = 2 1c = 0.5c = ( 0.5) ( 1) (0.5 1) 0.5 0.4 0.1P X P X P X= < − < < = − =≤ 0.1 (70 100)N ， 90 90 12 50 (1.30) 0.9032 (1.31) 0.9049 (1.32) 0.9066φ φ φ= = =， ， ξ ~ (70 100)Nξ ， ． 这说明成绩在 90 分以上（含 90 分）的学生人数约占全体参赛人数的 ， 因此参赛总人数约为 （人）． ⑵假定设奖的分数线为 分，则 ， 即 ，查表得 ，解得 ． 故设奖得分数线约为 分． 【答案】⑴设参赛总人数约为 人． ⑵奖得分数线约为 分． 【例37】如果随机变量 ，求 的值． 【考点】正态分布 【难度】3 星 【题型】解答 【关键字】无 【解析】由已知有 ． 由正态变量在 内取值的概率为 知 ． 由对称性知 ． 【答案】 【例38】灯泡厂生产的白炽灯寿命 （单位： ），已知 ，要使灯泡的 平均寿命为 的概率为 ，则灯泡的最低使用寿命应控制在 小时 以上． 【考点】正态分布 【难度】2 星 【题型】填空 【关键字】无 【解析】因为灯泡寿命 ，故 在 即 内取值的概率为 ，故灯泡的最低使用寿命应控制在 小时以上．答案 为 ． 【答案】 ． 【例39】某班有 名同学，一次考试后的数学成绩服从正态分布，平均分为 ，标准 差为 ，理论上说在 分到 分的人数是 ． 1 1( 90) ( 50) [1 (50 90)] (1 0.954) 0.0232 2P P Pξ ξ ξ= = − < < = − =≥ ≤ 2.3% 12 5220.023 ≈ x 70 50( ) 1 ( ) 1 ( ) 0.0957910 522 xP x P xξ ξ φ −= − < = − = ≈≥ 70( ) 0.904210 xφ − = 70 1.3110 x − ≈ 83.1x = 83.1 522 83.1 2~ ( ) 1N E Dξ µ σ ξ ξ= =， ， ( 1 1)P ξ− < < 1µ σ= = ( 2 , 2 )µ σ µ σ− + 95.4% ( 1 3) 0.954P ξ− < < = 1 1( 1 1) ( 1 3) 0.954 0.4772 2P Pξ ξ− < < = − < < = × = 0.477 ξ h 2~ (1000 30 )Nξ ， 1000h 99.7% _____ 2~ (1000 30 )Nξ ， ξ (1000 3 30 1000 3 30)− × + ×， (910 1090)， 99.7% 910 910 910 48 80 10 80 90 ______ 【考点】正态分布 【难度】3 星 【题型】填空 【关键字】无 【解析】数学成绩是 ， ． ． 分到 分的人数约为 ． 【答案】 ． 【例40】某城市从南郊某地乘公共汽车前往北区火车站有两条路线可走，第一条路线穿 过市区，路程较短，但交通拥挤，所需时间（单位为分）服从正态分布 ； 第二条路线沿环城公路走，路程较长，但交通阻塞少，所需时间服从正态分布 ⑴若只有 分钟可用，问应走哪条路线？ ⑵若只有 65 分钟可用，又应走哪条路线？ 【考点】正态分布 【难度】4 星 【题型】解答 【关键字】无 【解析】⑴走第一条路线，及时赶到的概率为 走第二条路线及时赶到的概率为 因此在这种情况下应走第二条路线． ⑵走第一条路线及时赶到的概率为 走第二条路线及时赶到的概率为 因此在这种情况下应走第一条路线． 【答案】⑴应走第二条路线． ⑵应走第一条路线． 板块三：随机变量的期望与方差 2~ (80 10 )X N ， 80 10µ σ= =， 1(80 90) ( ) ( ) 34.15%2P X P X P Xµ µ σ µ σ µ σ= + = − + =≤ ≤ ≤ ≤ ≤ ≤ 80 90 48 34.15% 16.392 16× = ≈ 16 ( )250, 10N ( )260, 4N 70 ( ) ( )70 50 0 50 70 500 70 2 0.977210 10 10P ξ − − −     < = Φ − Φ ≈ Φ = Φ =          ≤ ( ) ( )70 600 70 2.5 0.99384P ξ − < ≈ Φ = Φ =  ≤ ( ) ( )65 500 65 1.5 0.933210P ξ − < ≈ Φ = Φ =  ≤ ( ) ( )65 600 65 1.25 0.89444P ξ − < ≈ Φ = Φ =  ≤ 【例41】同时抛掷 枚均匀硬币 次，设 枚硬币正好出现 枚正面向上， 枚反面向 上的次数为 ，则 的数学期望是（ ） A． B． C． D． 【考点】数学期望 【难度】2 星 【题型】选择 【关键字】无 【解析】略 【答案】C； 【例42】（广东省揭阳市 2018 年高中毕业班高考调研测试） 一个篮球运动员投篮一次得 3 分的概率为 ，得 2 分的概率为 ，不得分的概率 为 （ 、 、 ），已知他投篮一次得分的数学期望为 2（不计其它得分 情况），则 的最大值为（ ） A． B． C． D． 【考点】数学期望 【难度】3 星 【题型】选择 【关键字】2018 年，广东省揭阳市高中毕业班高考调研测试 【解析】由已知得 ，即 ， ∴ ． 【答案】D； 【例1】 （2018 湖北高考） 某射手射击所得环数 的分布列如下： 7 8 9 10 已知 的期望 ，则 的值为 ． 【考点】离散型随机变量的期望与方差 【难度】1 星 【题型】填空 【关键词】2018 年，湖北高考 【解析】由数学期望的计算公式， 有 又由 ．解得 ． 【答案】 ； 【例43】一家保险公司在投保的 50 万元的人寿保险的保单中，估计每一千保单每年有 15 个理赔，若每一保单每年的营运成本及利润的期望值为 200 元，试求每一保 单的保费． 4 80 4 2 2 ξ ξ 20 25 30 40 a b c a b ( )0 1c∈ ， ab 1 48 1 24 1 12 1 6 3 2 0 2a b c+ + × = 3 2 2a b+ = 21 1 3 2 13 26 6 2 6 a bab a b + = ⋅ ⋅ =  ≤ ξ ξ P x 0.1 0.3 y ξ 8.9Eξ = y 7 8 0.1 9 0.3 10 8.9 7 10 5.4E x y x yξ = + ⋅ + ⋅ + ⋅ = ⇒ + = 0.1 0.3 1 0.6x y x y+ + + = ⇒ + = 0.4y = 0.4 【考点】数学期望 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】依题意知，利润的期望值 元． 设 表示保费，则理赔费为 ， 于是 解出 元． 即每一保单每年的保费应定在 元． 【例44】甲乙两人独立解出某一道数学题的概率依次为 ，已知该题被甲或 乙解出的概率为 ，甲乙两人同时解出该题的概率为 ，求： ⑴ ； ⑵解出该题的人数 的分布列及 ． 【考点】数学期望 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴设甲、乙两人解出该数学题分别为事件 和 ，则 ， 所以 ，即 解之得 ． ⑵ 的可能取值为 ， ， ， ． 列出分布列： 所以 ． 【例45】（08 湖南） 甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示 只要面试合格就签约．乙、丙则约定：两人面试都合格就一同签约，否则两人 都不签约．设每人面试合格的概率都是 ，且面试是否合格互不影响．求签约 人数 的数学期望． 【考点】数学期望 【难度】3 星 【题型】解答 【关键字】2018 年，湖南高考 【解析】略 【答案】用 A，B，C 分别表示事件甲、乙、丙面试合格．由题意知 A，B，C 相互独立，且 ( ) 200E X = x (500000 )x− − ( ) 0.985 0.015[ (500000 )] 200E X x x= + − − = 7700x = 7700 1 2 1 2( )P P P P>， 0.8 0.3 1 2P P， X EX A B 1 2( ) ( )P A P P B P= =， 1 ( ) 0.8 ( ) 0.3 P A B P A B  − ⋅ = ⋅ = 1 2 1 2 1 (1 )(1 ) 0.8 0.3 P P PP − − − =  = 1 20.6 0.5P P= =， X 0 1 2，， ( 0) 0.4 0.5 0.2P X = = × = ( 1) 0.6 0.5 0.4 0.5 0.5P X = = × + × = ( 2) 0.6 0.5 0.3P X = = × = X 0 1 2 P 0.2 0.5 0.3 0 0.2 0.5 1 0.3 2 1.1EX = × + × + × = 1 2 ξ ． 的可能取值为 ． = = ． ． ． 所以， 的期望 ． 【例46】学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有 人，会跳舞 的有 人，现从中选 人．设 为选出的人中既会唱歌又会跳舞的人数，且 ． ⑴求文娱队的人数； ⑵写出 的概率分布列并计算期望． 【考点】数学期望 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】设既会唱歌又会跳舞的有 人，则文娱队中共有 人， 那么只会一项的人数是 人． ⑴∵ ，∴ ．即 ． 化简： ．解得 ． 故文娱队共有 人． ⑵ 的可能取值为 ， ， ． 的概率分布列为： 于是期望为 ．（ ） 【例47】袋中编号为 ， ， ， ， 的五只小球，从中任取 只球，以 表示取出的 1( ) ( ) ( ) 2P A P B P C= = = ξ 0 1 2 3，， ， ( 0) ( ) ( ) ( )P P ABC P ABC P ABCξ = = + + ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )P A P B P C P A P B P C P A P B P C= + + 3 2 31 1 1 3( ) ( ) ( )2 2 2 8 = + + = ( 1) ( ) ( ) ( )P P ABC P ABC P ABCξ = = + + ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )P A P B P C P A P B P C P A P B P C+ + 3 3 31 1 1 3( ) ( ) ( )2 2 2 8 + + = 1( 2) ( ) ( ) ( ) ( ) 8P P ABC P A P B P Cξ = = = = 1( 3) ( ) ( ) ( ) ( ) 8P P ABC P A P B P Cξ = = = = ξ 3 3 1 10 1 2 3 18 8 8 8Eξ = × + × + × + × = 2 5 2 ξ 7( 0) 10P ξ > = ξ x (7 )x− (7 2 )x− 7( 0) 1 ( 0) 10P Pξ ξ> = − = = 3( 0) 10P ξ = = 2 7 2 2 7 C 3 C 10 x x − − = (7 2 )(6 2 ) 3 (7 )(6 ) 10 x x x x − − =− − 2x = 5 ξ 0 1 2，， 2 5 1 1( 2) C 10P ξ = = = 1 1 2 3 2 5 C C 3( 1) C 5P ξ = = = ξ ξ 0 1 2 P 3 10 3 5 1 10 3 3 1 40 1 210 5 10 5Eξ = × + × + × = 2 2 5Eξ ×= 1 2 3 4 5 3 ξ 球的最大号码，则 _________， _________． 【考点】期望与方差 【难度】2 星 【题型】填空 【关键字】无 【解析】略 【答案】 的可能取值为 ． ， ， ， 于是 ， ． 【例48】编号 的三位学生随意入座编号为 ， ， 的三个座位，每位学生坐一个 座位，设与座位编号相同的学生的个数是 ． ⑴ 求随机变量 的概率分布； ⑵ 求随机变量 的数学期望和方差． 【考点】期望与方差 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴ ， ， ． ∴随机变量 的概率分布为 ⑵ ． ． 【例49】（08 湖北） 袋中有 个大小相同的球，其中记上 号的有 个，记上 号的有 个 （ ）．现从袋中任取一球， 表示所取球的标号． ⑴求 的分布列，期望和方差； ⑵若 ， ， ，试求 的值． 【考点】期望与方差 【难度】4 星 【题型】解答 Eξ = Dξ = ξ 3 4 5， ， 2 2 3 5 C( 3) 0.1CP ξ = = = 2 3 3 5 C( 4) 0.3CP ξ = = = 2 4 3 5 C( 5) 0.6CP ξ = = = 0.1 3 0.3 4 0.6 5 4.5Eξ = × + × + × = 2 2 2(3 4.5) 0.1 (4 4.5) 0.3 (5 4.5) 0.6 0.315Dξ = − × + − × + − × = 1 2 3， ， 1 2 3 X X X 3 3 2 1( 0) 3P X = = = Α 1 3 3 3 C 1( 1) 2P X = = = Α 3 3 1 1( 3) 6P X = = = Α X X 0 1 3 P 1 3 1 2 1 6 1 1 1( ) 0 1 3 13 2 6E X = × + × + × = 2 2 21 1 1( ) (1 0) (1 1) (3 1) 13 2 6D X = − × + − × + − × = 20 0 10 n n 1 2 3 4n = ， ， ， ξ ξ a bη ξ= + 1Eη = 11Dη = a b， 【关键字】2018 年，湖北高考 【解析】略 【答案】⑴ 的分布列为： ∴ ⑵由 ，得 ，即 ．又 ，所以 当 时，由 ，得 ；当 时，由 ，得 ． ∴ 或 即为所求． 板块四：事件的独立性 【例50】判断下列各对事件是否是相互独立事件 ⑴容器内盛有 5 个白乒乓球和 3 个黄乒乓球，“从 8 个球中任意取出 个，取出的 是白球”与“从剩下的 个球中任意取出 个，取出的还是白球”． ⑵一筐内有 6 个苹果和 3 个梨，“从中任意取出 个，取出的是苹果”与“把取出的苹 果放回筐子，再从筐子中任意取出 个，取出的是梨”． ⑶甲组 名男生、 名女生；乙组 名男生、 名女生，今从甲、乙两组中各选 名 同学参加演讲比赛，“从甲组中选出 名男生”与“从乙组中选出 1 名女生”． 【考点】独立事件的判断 【难度】1 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴ “从 个球中任意取出 个，取出的是白球”的概率为 ， 若这一事件发生了，则“从剩下的 个球中任意取出 个，取出的仍是白球”的概率 为 ；若前一事件没有发生，则后一事件发生的概率为 ． 可见，前一事件是否发生对后一事件发生的概率有影响，所以二者不是相互独立事 件． ⑵ 由于把取出的苹果又放回筐子，故对“从中任意取出 个， 取出的是梨”的概率没有影响．所以二者是相互独立事件． ⑶“从甲组选出 名男生”这一事件是否发生，对“从乙组选出 名女生” 这一事件发生的概率没有影响，所以它们是相互独立事件． 【例51】若 与 相互独立，则下面选项中不是相互独立事件的是（ ） A． 与 B． 与 C． 与 D． 与 【考点】独立事件的判断 【难度】2 星 ξ ξ 0 1 2 3 4 P 1 2 1 20 1 10 3 20 1 5 1 1 1 3 10 1 2 3 4 1.5.2 20 10 20 5Eξ = × + × + × + × + × = 2 2 2 2 21 1 1 3 1(0 1.5) (1 1.5) (2 1.5) (3 1.5) (4 1.5) 2.75.2 20 10 20 5Dξ = − × + − × + − × + − × + − × = D a Dη ξ= 2 2 2.75 11a × = 2a = ± E aE bη ξ= + 2a = 2 1.5 1b× + = 2b = − 2a = − 2 1.5 1b− × + = 4b = 2 2 a b =  = − 2 4 a b = −  = 1 7 1 1 1 3 2 2 3 1 1 8 1 5 8 7 1 4 7 5 8 1 1 1 A B A A A B A B A B 【题型】解答 【关键字】无 【解析】从直观上讲，事件 独立即意味着彼此的发生与否不受对方影响． 而对于事件 ，其中一个发生即意味着另外一个一定不发生，于是 不 可能独立． 同理可以理解 与 ， 与 ， 与 独立． 若需从公式上给予一个严格证明，则需依据： 事件 独立 ． 当 与 相互独立，即 时， 对于 A 选项： ，故 不独立； 对于 B 选项： ， 故 独立； C，D 的独立证明是类似的，暂不详述． 【答案】A； 【例52】从一副不含大小王的扑克牌中任取一张， 记 {抽到 }， {抽到的牌是 黑色的}， 问事件 ， 是否独立? 【考点】独立事件的判断 【难度】2 星 【题型】解答 【关键字】无 【解析】略 【答案】事件 是独立的，证明如下： 一副扑克牌包含 13 种 4 种花色的牌一共 52 张． 抽到 包含 4 种情形， ； 抽到的牌是黑色的包含 26 种情形， ； 抽到黑色的 包含 2 种情形，于是 ； 于是 ． 于是事件 是独立的． 【例53】在一段时间内，甲去某地的概率是 ，乙去此地的概率是 ，假定两人的行动 相互之间没有影响，那么在这段时间内至少有 1 人去此地的概率是（ ） A． B． C． D． 【考点】依赖于独立性的概率计算 ,A B ,A A ,A A A B A B A B ,A B ( ) ( ) ( )P AB P A P B⇔ = ⋅ A B ( ) ( ) ( )P AB P A P B= ⋅ ( ) ( ) ( ) ( ) ( )0 1P AA P A P A P A P A= ≠ ⋅ = ⋅ −   ,A A ( ) ( ) ( ) ( ) ( ) ( )P AB P A P AB P A P A P B= − = − ⋅ ( ) ( ) ( ) ( )1P A P B P A P B= ⋅ − = ⋅   ,A B =A K =B A B ,A B K ( ) 4 1 52 13P A = = ( ) 26 1 52 2P B = = K ( ) 2 1 52 26P A B = = ( ) ( ) ( )P AB P A P B= ⋅ ,A B 1 4 1 5 3 20 1 5 2 5 9 20 【难度】2 星 【题型】选择 【关键字】无 【解析】至少有 1 人去此地的概率是 ． 【答案】C； 【例54】（2004 年辽宁高考） 甲乙两人独立地解同一问题，甲解决这个问题的概率是 ，乙解决这个问题的 概率是 ，那么恰好有 1 人解决这个问题的概率是（ ） A． B． C． D． 【考点】依赖于独立性的概率计算 【难度】2 星 【题型】选择 【关键字】2004 年，辽宁高考 【解析】恰好 1 人解决问题的概率即为仅有甲解决问题或者仅有乙解决问题． 前 者 的 概 率 为 ， 后 者 的 概 率 为 ． 于 是 答 案 为 ． 【答案】B； 【例55】从甲口袋内摸出 1 个白球的概率是 ，从乙口袋内摸出 1 个白球的概率是 ， 从两个口袋内各摸出 1 个球，那么 等于（ ） A．2 个球都是白球的概率 B．2 个球都不是白球的概率 C．2 个球不都是白球的概率 D．2 个球中恰好有 1 个是白球的概率 【考点】依赖于独立性的概率计算 【难度】2 星 【题型】选择 【关键字】无 【解析】不妨记从甲口袋摸出球的颜色为白球为 ， 从乙口袋摸出球的颜色为白球为 ，容易知道事件 为独立事件．于是 对于 A 选项： ； 对于 B 选项： ； 对于 C 选项： ； 对于 D 选项： ； 注记：对于事件 的交 ，有时候记为 ；事件的并 有时候记为 ． 某些参考资料中 仅表示不相容事件 的并． 1 1 21 1 14 5 5    − − ⋅ − =       1p 2p 1 2p p ( ) ( )1 2 2 11 1p p p p− + − 1 21 p p− ( )( )1 21 1 1p p− − − ( )1 21p p− ( )1 21 p p− ( ) ( )1 2 2 11 1p p p p− + − 1 3 1 2 5 6 A B ,A B ( ) ( ) ( ) 1 1 1 3 2 6P AB P A P B= ⋅ = ⋅ = ( ) ( ) ( ) 1 1 11 13 2 3P AB P A P B    = ⋅ = − ⋅ − =       ( ) ( ) ( ) ( ) 51 1 6P A B P A B P A P B= − = − ⋅ =  ( ) ( )( ) ( ) ( ) ( ) ( ) 1 2P AB AB P A P B P A P B= ⋅ + ⋅ = ,A B A B AB A B A B+ A B+ ,A B 【答案】C； 【例56】甲， 乙两人进行乒乓球比赛， 每局甲胜的概率为 ， 。问对甲而言， 采用三局二胜制有利， 还是采用五局三胜制有利． 设各局胜负相互独立． 【考点】依赖于独立性的概率计算 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】容易计算得知， 采用三局二胜制，甲的胜率为 ； 采用五局三胜制， 甲的胜率为 而 。 于是采用五局三胜制比较有利。 备注：直观上讲，对局数越多，所得的结果越可能体现选手的真实实力。在本 体中，甲选手的的实力要等同于或者强于乙，于是对局数越多，甲越可能凭实 力胜利。所谓的孤注一掷，是因为只实验一次，所以出现不合常理的可能性比 较大。 【例57】如图，开关电路中，某段时间内，开关 开或关的概率均为 ，且是相 互独立的，求这段时间内灯亮的概率． 【考点】依赖于独立性的概率计算 【难度】4 星 【题型】解答 【关键字】无 【解析】略 【答案】我们把“开关 合上”记为事件 ，“开关 合上”记为事件 ， “开关 合上”记为事件 ， 是相互独立事件且由已知，它们的概率都是 ，由物理学知识，要求灯亮，有两种可能性， 一个是 、 两开关合上，即事件 发生，另一个是 开关合上，即事件 发生， 也就是灯亮相当于事件 发生． 分别记“开关 合上”、“开关 合上”、“开关 合上”为事件 ，由已知， p 1 2p≥ ( )2 2 2 3 1 2 1 3 2P p p p p p= + − = − ( ) ( )25 4 4 3 3 5 4 3 2 5 51 1 6 15 10P p C p p C p p p p p= + − + − = − + ( ) ( )22 2 1 1 2 1 0P P p p p− = − − ≥ a b c、 、 1 2 c ba a A b B C C A B C、 、 1 2 a b AB c C AB C+ a b c A B C、 、 是相互独立事件且概率都是 ． 开关 、 合上或开关 合上时灯亮，所以这段时间内灯亮的概率为： ． 版块五：条件概率 【例58】把一枚硬币抛掷两次，事件 “第一次出现正面”，事件 “第二次出现反 面”， 则 ． 【考点】条件概率 【难度】2 星 【题型】填空 【关键字】无 【解析】 ． 【答案】 ； 【例59】掷两枚均匀的骰子，记 “点数不同”， “至少有一个是 点”，求 与 ． 【考点】条件概率 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】法一： 由题意得： ； ； （在第一次或第二次得到 点）； 故 ； ． 法二： 掷两枚骰子的所有基本事件有： ， 且每个基本事件发生的概率相同． 两次点数不同包含 个基本事件，其中至少含有一个 点的有 个， A B C、 、 1 2 a b c ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )P AB C P ABC P ABC P ABC P ABC P ABC P ABC P ABC P ABC+ = + + = + + + + ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )P A P B P C P A P B P C P A P B P C P A P B P C P A P B P C= + + + + 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 5 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 8 = × × + × × + × × + × × + × × = A = B = ( ) _____P B A = 1 1 ( ) 1( ) ( ) ( | )2 4 ( ) 2 P ABP A P AB P B A P A = = = =， ， 1 2 A = B = 6 ( | )P A B ( | )P B A 6 5 5( ) 6 6 6P A ×= =× 5 5 11( ) 1 ( ) 1 6 6 36P B P B ×= − = − =× 5 5( ) 26 6 18P A B = × =× 6 ( ) 1( | ) ( ) 3 P A BP B A P A = = ( ) 10( | ) ( ) 11 P A BP A B P B = = (1 1) (1 2) (1 6) (2 1) (2 2) (2 6) (6 1) (6 2) (6 6)     ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， 36 6 30− = 6 10 故 ； 在 含 有 的 个 基 本 事 件 中 ， 两 个 点 数 不 同 的 情 况 包 含 其 中 的 个 ， 故 ． 【例60】设某批产品有 是废品，而合格品中的 是一等品，任取一件产品是一等 品的概率是 ． 【考点】条件概率 【难度】2 星 【题型】填空 【关键字】无 【解析】设 “任取一件产品为一等品”， “任取一件产品为合格品”，所求概率为 ． 【答案】 ； 【例61】从 个整数中，任取一数，已知取出的—数是不大于 的数，求它是 2 或 3 的倍数的概率． 【考点】条件概率 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】用 A 表示“取出的数 ”，B 表示“取出的数是 2 或 3 的倍数”，问题即为求 ．不大于 的数中 2 或 3 的倍数共有 个（ 表示 不 超 过 的 最 大 整 数 ），于 是 ， 而 ， 因 此 由 公 式 ．直接求的话就是 ． 【例62】袋中装有 个白球， 个黑球，一次取出 个球，发现都是同一种颜色的， 问这种颜色是黑色的概率是多少? 【考点】条件概率 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】设 A 表示“取出 个球是同一种颜色”，B 表示“ 个球的颜色是黑色的”， 问题即为求 ． ， ， 10 1( | ) 30 3P B A = = 6 11 10 10( | ) 11P A B = 4% 75% A = B = ( ) ( ) ( | ) (1 0.04) 0.75 0.72P A P B P A B= ⋅ = − × = 0.72 1~100 50 50≤ ( | )P B A 50 50 50 50[ ] [ ] [ ] 332 3 6 + − = [ ]x x 33( ) 100P A B = 50( ) 100P A = ( )( | ) 0.66( ) P A BP B A P A = = 33( | ) 0.6650P B A = = 2 1n − 2n n n n ( | )P B A 2 4 1 C( ) C n n n n P A B − = 2 1 2 4 C +C( ) C n n n n n n P A −= 因此由公式 ． 直接求的话就是 ． 【例63】有两箱同类零件，第一箱内装 50 件，其中 10 件是一等品；第二箱内装 30 件， 其中 18 件是一等品．现从两箱中随意挑出一箱，然后从该箱中先后随机取出 两个零件（取出的零件均不放回），试求： ⑴先取出的零件是一等品的概率； ⑵在先取出的零件是一等品的条件下后取出的仍然是一等品的概率．（保留三位有 效数字） 【考点】条件概率 【难度】3 星 【题型】解答 【关键字】无 【解析】略 【答案】⑴两个箱子被挑到的概率都是 ，两个箱子先取出的是一等品的概率分别为 ，故先取出的是一等品的概率为 ． ⑵设 表示“第一次取出的是一等品”， 表示“第二次取出的是一等品”，问题即为 求 ． 两个箱子“两次抽到的都是一等品”的概率分别为： 因此 ． 故由公式 ． 2 2 1 2 C( ) 2( | ) ( ) C +C 3 n n n n n n P A BP B A P A − = = = 2 2 1 2 C 2( | ) C +C 3 n n n n n n P B A − = = 0.5 10 18( 0.2) ( 0.6)50 30 = =， 0.5 0.2 0.5 0.6 0.4⋅ + ⋅ = A B ( | )P B A 2 2 10 18 2 2 50 30 9 51 245 145 = =Α Α，Α Α 9 51( ) 0.5 0.5245 145P A B⋅ = ⋅ + ⋅ ( )( | ) ( ) P A BP B A P A ⋅= = 0.486