【数学】2020届一轮复习(理)通用版8-4直线、平面垂直的判定与性质作业
8.4 直线、平面垂直的判定与性质
挖命题
【考情探究】
考点
内容解读
5年考情
预测热度
考题示例
考向
关联考点
1.直线与平面垂直的判定与性质
①以立体几何的有关定义、公理和定理为出发点,认识和理解空间中线面垂直、面面垂直的有关性质与判定定理,并能够证明相关性质定理.
②能运用线面垂直、面面垂直的判定及性质定理证明空间图形的垂直关系
2016课标Ⅱ,19,12分
线面垂直的判定
翻折问题、二面角
★★★
2014课标Ⅰ,19,12分
线面垂直
的判定
二面角
2.平面与平面垂直的判定与性质
2017课标Ⅰ,18,12分
面面垂直的判定
二面角
★★★
2017课标Ⅲ,19,12分
面面垂直的
定义和判定
三棱锥的体积
及二面角
2016课标Ⅰ,18,12分
面面垂直的判定
二面角
2015课标Ⅰ,18,12分
面面垂直的判定
线面垂直的性质、
异面直线所成的角
分析解读 从近5年高考情况来看,线面、面面垂直的判定与性质是高考考查的重点内容,以选择题、填空题的形式出现时,常考查判断命题的真假;以解答题的形式出现时,常考查证明几何体中直线、平面垂直的位置关系.解答时要把定义、判定和性质结合起来,会进行线线、线面、面面问题的相互转化.
破考点
【考点集训】
考点一 直线与平面垂直的判定与性质
1.(2017河南中原名校联盟4月联考,4)已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是( )
A.α⊥β且m⊂α B.α⊥β且m∥α
C.m∥n且n⊥β D.m⊥n且n∥β
答案 C
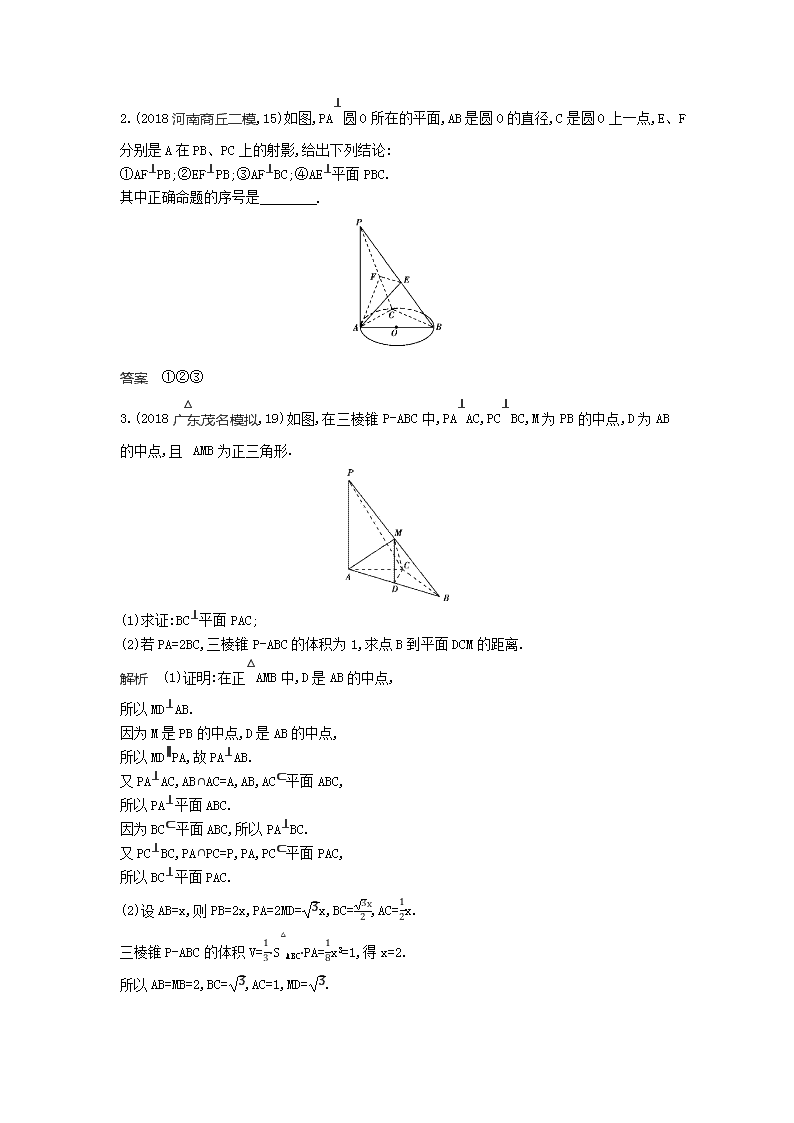
2.(2018河南商丘二模,15)如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上一点,E、F分别是A在PB、PC上的射影,给出下列结论:
①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.
其中正确命题的序号是 .
答案 ①②③
3.(2018广东茂名模拟,19)如图,在三棱锥P-ABC中,PA⊥AC,PC⊥BC,M为PB的中点,D为AB的中点,且△AMB为正三角形.
(1)求证:BC⊥平面PAC;
(2)若PA=2BC,三棱锥P-ABC的体积为1,求点B到平面DCM的距离.
解析 (1)证明:在正△AMB中,D是AB的中点,
所以MD⊥AB.
因为M是PB的中点,D是AB的中点,
所以MD∥PA,故PA⊥AB.
又PA⊥AC,AB∩AC=A,AB,AC⊂平面ABC,
所以PA⊥平面ABC.
因为BC⊂平面ABC,所以PA⊥BC.
又PC⊥BC,PA∩PC=P,PA,PC⊂平面PAC,
所以BC⊥平面PAC.
(2)设AB=x,则PB=2x,PA=2MD=3x,BC=3x2,AC=12x.
三棱锥P-ABC的体积V=13·S△ABC·PA=18x3=1,得x=2.
所以AB=MB=2,BC=3,AC=1,MD=3.
所以S△BCD=12S△ABC=12×12×3×1=34.
由(1)知MD∥PA,PA⊥平面ABC,所以MD⊥DC.
在△ABC中,CD=12AB=1,
所以S△MCD=12MD·CD=12×3×1=32.
设点B到平面DCM的距离为h.
因为VM-BCD=VB-MCD,
所以13S△BCD·MD=13S△MCD·h,即13×34×3=13×32×h.
所以h=32.故点B到平面DCM的距离为32.
考点二 平面与平面垂直的判定与性质
1.(2018湖北重点中学协作体4月联考,5)设m,n是平面α内的两条不同直线,l1,l2是平面β内两条相交直线,则α⊥β 的一个充分不必要条件是( )
A.l1⊥m,l1⊥n B.m⊥l1,m⊥l2
C.m⊥l1,n⊥l2 D.m∥n,l1⊥n
答案 B
2.(2017福建泉州二模,16)如图,一张A4纸的长、宽分别为22a,2a,A,B,C,D分别是其四条边的中点.现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体.下列关于该多面体的命题,正确的是 .(写出所有正确命题的序号)
①该多面体是三棱锥;
②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;
④该多面体外接球的表面积为5πa2.
答案 ①②③④
3.(2018辽宁锦州模拟,18)如图,在四棱锥P-ABCD中,AD∥BC,AD⊥CD,Q是AD的中点,M是棱PC的中点,PA=PD=2,BC=12AD=1,CD=3,PB=6.
(1)求证:PA∥平面MQB;
(2)求证:平面PAD⊥平面ABCD;
(3)求三棱锥B-PQM的体积.
解析 (1)证明:如图,连接AC交BQ于N,连接MN,CQ.
∵BC=12AD,AD∥BC,Q是AD的中点,∴AQ∥BC,且AQ=BC,∴四边形ABCQ是平行四边形,∴N是AC的中点.∵M是棱PC的中点,∴MN∥PA.∵PA⊄平面MQB,MN⊂平面MQB,∴PA∥平面MQB.
(2)证明:∵AD∥BC,BC=12AD=1,Q是AD的中点,∴四边形BCDQ为平行四边形,∴CD∥BQ.∵AD⊥CD,∴QB⊥AD.又PA=PD=2,AD=2,Q是AD的中点,∴PQ=3.又QB=CD=3,PB=6,∴PB2=PQ2+QB2.由勾股定理的逆定理可知PQ⊥QB.又PQ∩AD=Q,∴BQ⊥平面PAD.又BQ⊂平面ABCD,∴平面PAD⊥平面ABCD.
(3)∵PA=PD=2,Q是AD的中点,∴PQ⊥AD.∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.又M是棱PC的中点,故VB-PQM=12VP-BQC=12×13×12×1×3×3=14.
炼技法
【方法集训】
方法1 证明直线与平面垂直的方法
1.(2017山西五校联考,19)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE∶EB=7∶2,点F、G、M分别为线段PA、PD、BC的中点.
(1)求证:PE⊥平面ABCD;
(2)若平面EFG与直线CD交于点N,求二面角P-MN-A的余弦值.
解析 (1)证明:在等腰△APB中,cos∠ABP=12PBAB=13,则由余弦定理可得PE2=29×32+22-2×29×3×2×13=329,∴PE=423.∴PE2+BE2=4=PB2,∴PE⊥AB.
∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PE⊥平面ABCD.
(2)连接EN,由已知可得EN∥AD.所以EN⊥AB.由(1)可知PE⊥EN.
以E为坐标原点,直线EP、EB、EN分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,则P423,0,0,M0,23,1,N(0,0,2),从而PM=-423,23,1,MN=0,-23,1.
设平面PMN的法向量为n=(x,y,z),
则n·PM=0,n·MN=0,
即-423x+23y+z=0,-23y+z=0,
令y=3,可得n=322,3,2.
由(1)知平面AMN的一个法向量为EP=423,0,0,
∴cos
=4423×352=33535,
由图可知二面角P-MN-A的平面角为锐角,
故二面角P-MN-A的余弦值为33535.
2.(2018河北“五个一名校联盟”联考,19)如图1,在直角梯形ABCD中,∠ADC=90°,AB∥CD,AD=CD=12AB=2,E为AC的中点,将△ACD沿AC折起,使折起后的平面ACD与平面ABC垂直,如图2.在图2所示的几何体D-ABC中:
(1)求证:BC⊥平面ACD;
(2)点F在棱CD上,且满足AD∥平面BEF,求几何体F-BCE的体积.
解析 (1)证明:∵AC=AD2+CD2=22,
∠BAC=∠ACD=45°,AB=4,
∴在△ABC中,BC2=AC2+AB2-2AC·AB·cos 45°=8,
∴AB2=16=AC2+BC2,
∴AC⊥BC,(4分)
∵平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,
∴BC⊥平面ACD.(6分)
(2)∵AD∥平面BEF,AD⊂平面ACD,平面ACD∩平面BEF=EF,∴AD∥EF,(7分)
∵E为AC的中点,∴EF为△ACD的中位线,(8分)
∵VF-BCE=VB-CEF=13S△CEF·BC,S△CEF=14S△ACD=14×12×2×2=12,∴VF-BCE=13×12×22=23.(12分)
方法2 证明平面与平面垂直的方法
1.(2017河南百校联盟联考,11)如图,已知等腰直角三角形ABC中,AB=AC,将△ABC沿斜边BC向上翻转,与原图形构成几何体A1-ABC,其外接球表面积为4π,设二面角A1-BC-A的平面角为α,若O为BC的中点,点P,Q分别为线段OA1,AB的中点,则当PQ=32时,角α等于( )
A.π3 B.π2 C.2π3 D.3π4
答案 B
2.(2018河南郑州二模,19)如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,△DAB≌△DCB,E为线段BD上一点,且EB=ED=EC=BC,延长CE交AD于F.
(1)若G为PD的中点,求证:平面PAD⊥平面CGF;
(2)若BC=2,PA=3,求平面BCP与平面DCP所成锐二面角的余弦值.
解析 (1)证明:在△BCD中,EB=ED=EC=BC,故∠BCD=π2,∠CBE=∠CEB=π3,
连接AE,∵△DAB≌△DCB,∴△EAB≌△ECB,
从而有∠FED=∠BEC=∠AEB=π3,AE=CE=DE.(3分)
∴∠AEF=∠FED=π3,故EF⊥AD,AF=FD.
又PG=GD,∴FG∥PA.
又PA⊥平面ABCD,故GF⊥平面ABCD,
∴GF⊥AD,又GF∩EF=F,故AD⊥平面CFG.
又AD⊂平面PAD,∴平面PAD⊥平面CGF.(6分)
(2)以点A为坐标原点建立如图所示的空间直角坐标系,
则A(0,0,0),B(2,0,0),C(3,3,0),D(0,23,0),P(0,0,3).
故BC=(1,3,0),CP=(-3,-3,3),CD=(-3,3,0).
设平面BCP的一个法向量为n1=(1,y1,z1),
则1+3y1=0,-3-3y1+3z1=0,解得y1=-33,z1=23,即n1=1,-33,23.(9分)
设平面DCP的一个法向量为n2=(1,y2,z2),
则-3+3y2=0,-3-3y2+3z2=0,解得y2=3,z2=2,即n2=(1,3,2).
从而平面BCP与平面DCP所成锐二面角的余弦值为|n1·n2||n1||n2|=43169×8=24.(12分)
3.如图,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.
(1)求证:平面PAC⊥平面ABC;
(2)求二面角D-AP-C的正弦值.
解析 (1)证明:因为D是斜边AB的中点,
所以BD=DA.
因为△PDB是等边三角形,
所以BD=DP=BP,则BD=DA=DP,
因此△APB为直角三角形,即PA⊥BP.
又PA⊥PC,PC∩BP=P,
所以PA⊥平面PCB.
因为BC⊂平面PCB,所以PA⊥BC.
又AC⊥BC,PA∩AC=A,所以BC⊥平面PAC.
因为BC⊂平面ABC,所以平面PAC⊥平面ABC.
(2)由(1)知PA⊥PB,
又PA⊥PC,故∠BPC即为二面角D-AP-C的平面角.
由(1)知BC⊥平面PAC,则BP⊥PC.
在Rt△BPC中,BC=4,BP=BD=10,
所以sin∠BPC=BCBP=410=25,
即二面角D-AP-C的正弦值为25.
过专题
【五年高考】
A组 统一命题·课标卷题组
考点一 直线与平面垂直的判定与性质
1.(2016课标Ⅱ,19,12分)如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=54,EF交BD于点H.将△DEF沿EF折到△D'EF的位置,OD'=10.
(1)证明:D'H⊥平面ABCD;
(2)求二面角B-D'A-C的正弦值.
解析 (1)证明:由已知得AC⊥BD,AD=CD.
又由AE=CF得AEAD=CFCD,故AC∥EF.
因此EF⊥HD,从而EF⊥D'H.(2分)
由AB=5,AC=6得DO=BO=AB2-AO2=4.
由EF∥AC得OHDO=AEAD=14.
所以OH=1,D'H=DH=3.
于是D'H2+OH2=32+12=10=D'O2,
故D'H⊥OH.(4分)
又D'H⊥EF,而OH∩EF=H,
所以D'H⊥平面ABCD.(5分)
(2)如图,以H为坐标原点,HF的方向为x轴正方向,建立空间直角坐标系H-xyz.则H(0,0,0),A(-3,-1,0),B(0,-5,0),C(3,-1,0),D'(0,0,3),
AB=(3,-4,0),AC=(6,0,0),AD'=(3,1,3).(6分)
设m=(x1,y1,z1)是平面ABD'的法向量,
则m·AB=0,m·AD'=0,即3x1-4y1=0,3x1+y1+3z1=0,
所以可取m=(4,3,-5).(8分)
设n=(x2,y2,z2)是平面ACD'的法向量,
则n·AC=0,n·AD'=0,即6x2=0,3x2+y2+3z2=0,
所以可取n=(0,-3,1).(10分)
于是cos=m·n|m||n|=-1450×10=-7525,
sin=29525.
因此二面角B-D'A-C的正弦值是29525.(12分)
思路分析 (1)利用已知条件及翻折的性质得出D'H⊥EF,利用勾股定理逆定理得出D'H⊥OH,从而得出结论;
(2)在第(1)问的基础上建立恰当的空间直角坐标系,从而求出两个半平面的法向量,利用向量的夹角公式求其余弦值,从而求出正弦值,最后转化为二面角的正弦值.
2.(2014课标Ⅰ,19,12分)如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值.
解析 (1)证明:连接BC1,交B1C于点O,连接AO.因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.
又AB⊥B1C,所以B1C⊥平面ABO.由于AO⊂平面ABO,故B1C⊥AO.又B1O=CO,故AC=AB1.
(2)因为AC⊥AB1,且O为B1C的中点,所以AO=CO.
又因为AB=BC,所以△BOA≌△BOC.故OA⊥OB,从而OA,OB,OB1两两垂直.
以O为坐标原点,OB的方向为x轴正方向,|OB|为单位长,建立如图所示的空间直角坐标系
O-xyz.
因为∠CBB1=60°,所以△CBB1为等边三角形,又AB=BC,则A0,0,33,B(1,0,0),B10,33,0,C0,-33,0.
AB1=0,33,-33,A1B1=AB=1,0,-33,B1C1=BC=-1,-33,0.
设n=(x,y,z)是平面AA1B1的法向量,
则n·AB1=0,n·A1B1=0,即33y-33z=0,x-33z=0.
所以可取n=(1,3,3).
设m是平面A1B1C1的法向量,
则m·A1B1=0,m·B1C1=0.
同理可取m=(1,-3,3).
则cos=n·m|n||m|=17.
易知二面角A-A1B1-C1为锐二面角,
所以二面角A-A1B1-C1的余弦值为17.
方法点拨 在求解或证明过程中,通常会用到一些初中阶段学习的平面几何知识,如三角形中位线的性质、菱形的性质,等腰三角形的性质,相似(全等)三角形的判定与性质等,在复习时应予以关注.
考点二 平面与平面垂直的判定与性质
1.(2018课标Ⅰ,18,12分)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
解析 (1)证明:由已知可得BF⊥EF,
又已知BF⊥PF,且PF、EF⊂平面PEF,PF∩EF=F,
所以BF⊥平面PEF,
又BF⊂平面ABFD,
所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.
由(1)得,PH⊥平面ABFD.
以H为坐标原点,HF的方向为y轴正方向,|BF|为单位长,建立如图所示的空间直角坐标系H-xyz.
由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=3,
又PF=1,EF=2,故PE⊥PF,
可得PH=32,EH=32,
则H(0,0,0),P0,0,32,D-1,-32,0,DP=1,32,32,HP=0,0,32为平面ABFD的法向量.
设DP与平面ABFD所成角为θ,则sin θ=HP·DP|HP||DP|=343=34.
所以DP与平面ABFD所成角的正弦值为34.
易错警示 利用空间向量求线面角的注意事项
(1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角即为所求.
(2)若求线面角的余弦值,要注意利用平方关系sin2θ+cos2θ=1求出其值,不要误以为直线的方向向量与平面的法向量所夹角的余弦值为所求.
2.(2017课标Ⅰ,18,12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.
解析 本题考查了立体几何中面面垂直的证明和二面角问题.
(1)证明:由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,
又AP∩PD=P,
从而AB⊥平面PAD.
又AB⊂平面PAB,
所以平面PAB⊥平面PAD.
(2)在平面PAD内作PF⊥AD,垂足为F.
由(1)可知,AB⊥平面PAD,
故AB⊥PF,
又AD∩AB=A,可得PF⊥平面ABCD.
以 F为坐标原点,FA的方向为x轴正方向,|AB|为单位长,建立如图所示的空间直角坐标系F-xyz.
由(1)及已知可得A22,0,0,P0,0,22,B22,1,0,C-22,1,0.
所以PC=-22,1,-22,CB=(2,0,0),PA=22,0,-22,AB=(0,1,0).
设n=(x1,y1,z1)是平面PCB的法向量,则
n·PC=0,n·CB=0,即-22x1+y1-22z1=0,2x1=0.
可取n=(0,-1,-2).
设m=(x2,y2,z2)是平面PAB的法向量,则
m·PA=0,m·AB=0,即22x2-22z2=0,y2=0.
可取m=(1,0,1).
则cos=n·m|n||m|=-33.
易知二面角A-PB-C为钝二面角,
所以二面角A-PB-C的余弦值为-33.
方法总结 面面垂直的证明及向量法求解二面角.
(1)面面垂直的证明
证明两个平面互相垂直,可以在一个平面内找一条直线l,证明直线l垂直于另一平面.
(2)利用空间向量求解几何体中的二面角的余弦值.
建立空间直角坐标系,找到点的坐标,求出两个半平面的法向量n1,n2,设二面角的大小为θ,则|cos θ|=|n1·n2||n1||n2|,再根据二面角的范围判断二面角余弦值的正负情况.
3.(2017课标Ⅲ,19,12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.
解析 本题考查面面垂直的证明,二面角的求法.
(1)证明:由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.所以平面ACD⊥平面ABC.
(2)由题设及(1)知,OA,OB,OD两两垂直.以O为坐标原点,OA的方向为x轴正方向,|OA|为单位长,建立如图所示的空间直角坐标系O-xyz.则A(1,0,0),B(0,3,0),C(-1,0,0),D(0,0,1).
由题设知,四面体ABCE的体积为四面体ABCD的体积的12,从而E到平面ABC的距离为D到平面ABC的距离的12,即E为DB的中点,得E0,32,12.故AD=(-1,0,1),AC=(-2,0,0),AE=-1,32,12.
设n=(x,y,z)是平面DAE的法向量,
则n·AD=0,n·AE=0,即-x+z=0,-x+32y+12z=0.可取n=1,33,1.
设m是平面AEC的法向量,则m·AC=0,m·AE=0.
同理可取m=(0,-1,3).
则cos=n·m|n||m|=77.易知二面角D-AE-C为锐二面角,所以二面角D-AE-C的余弦值为77.
方法总结 证明面面垂直最常用的方法是证明其中一个平面经过另一个平面的一条垂线,即在一个平面内,找一条直线,使它垂直于另一个平面.用空间向量法求二面角的余弦值时,要判断二面角是钝角还是锐角.
4.(2016课标Ⅰ,18,12分)
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(1)证明:平面ABEF⊥平面EFDC;
(2)求二面角E-BC-A的余弦值.
解析 (1)证明:由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC.(2分)
又AF⊂平面ABEF,故平面ABEF⊥平面EFDC.(3分)
(2)过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF.
以G为坐标原点,GF的方向为x轴正方向,|GF|为单位长,建立如图所示的空间直角坐标系G-xyz.(6分)
0
由(1)知∠DFE为二面角D-AF-E的平面角,故∠DFE=60°,则|DF|=2,|DG|=3,可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,3).
由已知得,AB∥EF,所以AB∥平面EFDC.(8分)
又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF.
由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°.从而可得
C(-2,0,3).
所以EC=(1,0,3),EB=(0,4,0),AC=(-3,-4,3),AB=(-4,0,0).(10分)
设n=(x,y,z)是平面BCE的法向量,则n·EC=0,n·EB=0,即x+3z=0,4y=0.所以可取n=(3,0,-3).
设m是平面ABCD的法向量,则m·AC=0,m·AB=0.
同理可取m=(0,3,4).则cos =n·m|n||m|=-21919.
又易知二面角E-BC-A为钝二面角,
故二面角E-BC-A的余弦值为-21919.(12分)
思路分析 (1)根据已知条件证出AF⊥平面EFDC,进而得出平面ABEF⊥平面EFDC;(2)根据证得的垂直关系建立空间直角坐标系,求出平面BCE、平面ABCD的法向量,进而可求得二面角E-BC-A的余弦值.
方法总结 对于立体几何问题的求解,首先要熟练掌握平行与垂直的判定与性质,对于面面垂直的证明,寻找平面的垂线往往是解题的关键.
5.(2015课标Ⅰ,18,12分)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC;
(2)求直线AE与直线CF所成角的余弦值.
解析 (1)证明:连接BD.设BD∩AC=G,连接EG,FG,EF.
在菱形ABCD中,不妨设GB=1.由∠ABC=120°,可得AG=GC=3.
由BE⊥平面ABCD,AB=BC,可知AE=EC.
又AE⊥EC,所以EG=3,
且EG⊥AC.
在Rt△EBG中,可得BE=2,故DF=22.
在Rt△FDG中,可得FG=62.
在直角梯形BDFE中,
由BD=2,BE=2,DF=22,
可得EF=322.
从而EG2+FG2=EF2,所以EG⊥FG.
又AC∩FG=G,可得EG⊥平面AFC.
因为EG⊂平面AEC,所以平面AEC⊥平面AFC.(6分)
(2)如图,以G为坐标原点,分别以GB,GC的方向为x轴,y轴正方向,|GB|为单位长,建立空间直角坐标系G-xyz.
由(1)可得A(0,-3,0),E(1,0,2),
F-1,0,22,C(0,3,0),所以AE=(1,3,2),CF=-1,-3,22.(10分)
故cos=AE·CF|AE||CF|=-33.
所以直线AE与直线CF所成角的余弦值为33.(12分)
B组 自主命题·省(区、市)卷题组
考点一 直线与平面垂直的判定与性质
1.(2018北京,16,14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=5,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B-CD-C1的余弦值;
(3)证明:直线FG与平面BCD相交.
解析 (1)证明:在三棱柱ABC-A1B1C1中,
因为CC1⊥平面ABC,
所以四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
所以AC⊥EF.
因为AB=BC,
所以AC⊥BE.
所以AC⊥平面BEF.
(2)由(1)知AC⊥EF,AC⊥BE,EF∥CC1.
又CC1⊥平面ABC,所以EF⊥平面ABC.
因为BE⊂平面ABC,所以EF⊥BE.
如图建立空间直角坐标系E-xyz.
由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1).
所以BC=(-1,-2,0),BD=(1,-2,1).
设平面BCD的法向量为n=(x0,y0,z0),
则n·BC=0,n·BD=0,即x0+2y0=0,x0-2y0+z0=0.
令y0=-1,则x0=2,z0=-4.
于是n=(2,-1,-4).
又因为平面CC1D的一个法向量为EB=(0,2,0),
所以cos=n·EB|n||EB|=-2121.
由题知二面角B-CD-C1为钝角,所以其余弦值为-2121.
(3)证明:由(2)知平面BCD的一个法向量为n=(2,-1,-4),FG=(0,2,-1).
因为n·FG=2×0+(-1)×2+(-4)×(-1)=2≠0,
所以直线FG与平面BCD相交.
2.(2015湖北,19,12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.
(1)证明:PB⊥平面DEF.试判断四面体DBEF是不是鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为π3,求DCBC的值.
解析 解法一:(1)因为PD⊥底面ABCD,所以PD⊥BC,
由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,
所以BC⊥平面PCD,而DE⊂平面PCD,所以BC⊥DE.
又因为PD=CD,点E是PC的中点,所以DE⊥PC.
而PC∩BC=C,所以DE⊥平面PBC.
而PB⊂平面PBC,所以PB⊥DE.
又PB⊥EF,DE∩EF=E,
所以PB⊥平面DEF.
由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,
即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.
(2)如图,在面PBC内,延长BC与FE交于点G,则DG是平面DEF与平面ABCD的交线.
由(1)知,PB⊥平面DEF,所以PB⊥DG.
又因为PD⊥底面ABCD,所以PD⊥DG.
而PD∩PB=P,所以DG⊥平面PBD.
故∠BDF是面DEF与面ABCD所成二面角的平面角,
设PD=DC=1,BC=λ,有BD=1+λ2,
在Rt△PDB中,由DF⊥PB,得∠DPF=∠FDB=π3,
则tanπ3=tan∠DPF=BDPD=1+λ2=3,解得λ=2.
所以DCBC=1λ=22.
故当面DEF与面ABCD所成二面角的大小为π3时,DCBC=22.
解法二:(1)如图,以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.
设PD=DC=1,BC=λ,则D(0,0,0),P(0,0,1),B(λ,1,0),
C(0,1,0),PB=(λ,1,-1),点E是PC的中点,
所以E0,12,12,DE=0,12,12,
于是PB·DE=0,即PB⊥DE.
又已知EF⊥PB,而DE∩EF=E,
所以PB⊥平面DEF.
因PC=(0,1,-1),DE·PC=0,
则DE⊥PC,所以DE⊥平面PBC.
由DE⊥平面PBC,PB⊥平面DEF,
可知四面体BDEF的四个面都是直角三角形,
即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB.
(2)因为PD⊥平面ABCD,所以DP=(0,0,1)是平面ABCD的一个法向量;
由(1)知,PB⊥平面DEF,所以BP=(-λ,-1,1)是平面DEF的一个法向量.
若面DEF与面ABCD所成二面角的大小为π3,
则cosπ3=BP·DP|BP|·|DP|
=1λ2+2=12,
解得λ=2,
所以DCBC=1λ=22.
故当面DEF与面ABCD所成二面角的大小为π3时,DCBC=22.
考点二 平面与平面垂直的判定与性质
(2015北京,17,14分)如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
(1)求证:AO⊥BE;
(2)求二面角F-AE-B的余弦值;
(3)若BE⊥平面AOC,求a的值.
解析 (1)证明:因为△AEF是等边三角形,O为EF的中点,所以AO⊥EF.
又因为平面AEF⊥平面EFCB,AO⊂平面AEF,
所以AO⊥平面EFCB.
所以AO⊥BE.
(2)取BC中点G,连接OG.
由题设知EFCB是等腰梯形,
所以OG⊥EF.
由(1)知AO⊥平面EFCB,
又OG⊂平面EFCB,
所以OA⊥OG.
如图建立空间直角坐标系O-xyz,
则E(a,0,0),A(0,0,3a),B(2,3(2-a),0),EA=(-a,0,3a),BE=(a-2,3(a-2),0).
设平面AEB的法向量为n=(x,y,z),
则n·EA=0,n·BE=0,即-ax+3az=0,(a-2)x+3(a-2)y=0.
令z=1,则x=3,y=-1.
于是n=(3,-1,1).
平面AEF的法向量为p=(0,1,0).
所以cos=n·p|n||p|=-55.
由题设知二面角F-AE-B为钝角,所以它的余弦值为-55.
(3)因为BE⊥平面AOC,所以BE⊥OC,即BE·OC=0.
因为BE=(a-2,3(a-2),0),OC=(-2,3(2-a),0),
所以BE·OC=-2(a-2)-3(a-2)2.
由BE·OC=0及0=n1·n2|n1|·|n2|=31·(6-m)2+62+32=3(6-m)2+45.
而二面角P-QD-A的余弦值为37,因此3(6-m)2+45=37,解得m=4,或m=8(舍去),此时Q(6,4,0).
设DP=λDD1(0<λ≤1),而DD1=(0,-3,6),由此得点P(0,6-3λ,6λ),所以PQ=(6,3λ-2,-6λ).
因为PQ∥平面ABB1A1,且平面ABB1A1的一个法向量是n3=(0,1,0),所以PQ·n3=0,即3λ-2=0,亦即λ=23,从而P(0,4,4).
于是,将四面体ADPQ视为以△ADQ为底面的三棱锥P-ADQ,则其高h=4.故四面体ADPQ的体积V=13S△ADQ·h=13×12×6×6×4=24.
解法二:(1)证明:如图a,取A1A的中点R,连接PR,BR.因为A1A,D1D是梯形A1ADD1的两腰,P是D1D的中点,所以PR∥AD,于是由AD∥BC知,PR∥BC,所以P,R,B,C四点共面.
由题设知,BC⊥AB,BC⊥A1A,所以BC⊥平面ABB1A1,因此BC⊥AB1.①
因为tan∠ABR=ARAB=36=A1B1A1A=tan∠A1AB1,所以∠ABR=∠A1AB1,因此∠ABR+∠BAB1=∠A1AB1+∠BAB1=90°,
于是AB1⊥BR.再由①即知AB1⊥平面PRBC.
又PQ⊂平面PRBC,故AB1⊥PQ.
图a
图b
(2)如图b,过点P作PM∥A1A交AD于点M,则PM∥平面ABB1A1.②
因为A1A⊥平面ABCD,所以PM⊥平面ABCD.过点M作MN⊥QD于点N,连接PN,则PN⊥QD,∠PNM为二面角P-QD-A的平面角,所以cos∠PNM=37,即MNPN=37,从而PMMN=403.③
连接MQ,由PQ∥平面ABB1A1及②知,平面PQM∥平面ABB1A1,所以MQ∥AB.又ABCD是正方形,所以ABQM为矩形,故MQ=AB=6.
设MD=t,则MN=MQ·MDMQ2+MD2=6t36+t2.④
过点D1作D1E∥A1A交AD于点E,则AA1D1E为矩形,所以D1E=A1A=6,AE=A1D1=3,因此ED=AD-AE=3.于是PMMD=D1EED=63=2,所以PM=2MD=2t.
再由③,④得36+t23=403,解得t=2,因此PM=4.故四面体ADPQ的体积V=13S△ADQ·PM=13×12×6×6×4=24.
2.(2014广东,18,13分)如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角D-AF-E的余弦值.
解析 (1)证明:∵PD⊥平面ABCD,∴PD⊥AD,
又CD⊥AD,PD∩CD=D,
∴AD⊥平面PCD,∴AD⊥PC,
又AF⊥PC,AF∩AD=A,
∴PC⊥平面ADF,即CF⊥平面ADF.
(2)解法一:设AB=1,则Rt△PDC中,CD=1,∵∠DPC=30°,
∴PC=2,PD=3,由(1)知CF⊥DF,
∴DF=32,∴CF=12,又FE∥CD,
∴DEPD=CFPC=14,∴DE=34,同理,EF=34CD=34,
如图所示,以D为原点,建立空间直角坐标系,则A(0,0,1),
E34,0,0,F34,34,0,P(3,0,0),C(0,1,0).
设m=(x,y,z)是平面AEF的法向量,
则m⊥AE,m⊥EF,又 AE=34,0,-1,EF=0,34,0,
∴m·AE=34x-z=0,m·EF=34y=0,
令x=4,得z=3,故m=(4,0,3),
由(1)知平面ADF的一个法向量为PC=(-3,1,0),设二面角D-AF-E的平面角为θ,可知θ为锐角,
cos θ=|cos|=|m·PC||m|·|PC|=4319×2=25719,故二面角D-AF-E的余弦值为25719.
解法二:设AB=1,
∵CF⊥平面ADF,∴CF⊥DF.
∴在△CFD中,DF=32,
∵CD⊥AD,CD⊥PD,
∴CD⊥平面ADE.又∵EF∥CD,
∴EF⊥平面ADE.∴EF⊥AE,
∴在△DEF中,DE=34,EF=34,
在△ADE中,AE=194,在△ADF中,AF=72.
由VA-DEF=13·S△ADE·EF=13·S△ADF·hE-ADF,
解得hE-ADF=38,
设△AEF的边AF上的高为h,
由S△AEF=12·EF·AE=12·AF·h,解得h=34×13314,
设二面角D-AF-E的平面角为θ,可知θ为锐角.
则sin θ=hE-ADFh=38×43×14133=13319,
∴cos θ=25719.
考点二 平面与平面垂直的判定与性质
1.(2014福建,17,13分)在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
解析 (1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,AB⊥BD,
∴AB⊥平面BCD.
又CD⊂平面BCD,∴AB⊥CD.
(2)过点B在平面BCD内作BE⊥BD,如图.
由(1)知AB⊥平面BCD,又BE⊂平面BCD,BD⊂平面BCD,
∴AB⊥BE,AB⊥BD.
以B为坐标原点,分别以BE,BD,BA的方向为x轴,y轴,z轴的正方向建立空间直角坐标系.
依题意,得B(0,0,0),C(1,1,0),D(0,1,0),A(0,0,1),M0,12,12,
则BC=(1,1,0),BM=0,12,12,AD=(0,1,-1).
设平面MBC的法向量为n=(x0,y0,z0),
则n·BC=0,n·BM=0,即x0+y0=0,12y0+12z0=0,
取z0=1,得平面MBC的一个法向量为n=(1,-1,1).
设直线AD与平面MBC所成角为θ,
则sin θ=|cos|=|n·AD||n|·|AD|=63,
即直线AD与平面MBC所成角的正弦值为63.
评析 本题主要考查空间直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想.
2.(2014江西,19,12分)如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB=2,PC=2,问AB为何值时,四棱锥P-ABCD的体积最大?并求此时平面BPC
与平面DPC夹角的余弦值.
解析 (1)证明:ABCD为矩形,故AB⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以AB⊥平面PAD,故AB⊥PD.
(2)过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.故PO⊥平面ABCD,BC⊥平面POG,
所以BC⊥PG.
在Rt△BPC中,PG=233,GC=263,BG=63.
设AB=m,则OP=PG2-OG2=43-m2,
故四棱锥P-ABCD的体积V=13·6·m·43-m2=m38-6m2.
因为m8-6m2=8m2-6m4=-6m2-232+83,
故当m=63,即AB=63时,四棱锥P-ABCD的体积最大.
此时,建立如图所示的坐标系,各点的坐标为O(0,0,0),B63,-63,0,C63,263,0,D0,263,0,P0,0,63.
故PC=63,263,-63,BC=(0,6,0),CD=-63,0,0.
设平面BPC的一个法向量为n1=(x,y,1),则由n1⊥PC,n1⊥BC得63x+263y-63=0,6y=0,解得x=1,y=0,所以n1=(1,0,1).
同理可求出平面DPC的一个法向量为n2=0,12,1.
从而平面BPC与平面DPC的夹角θ的余弦值为cos θ=|n1·n2||n1||n2|=12×14+1=105.
评析 本题考查面面垂直的性质定理、线线垂直的判定、空间几何体的体积以及二面角的求解等基础知识,考查空间想象能力、推理论证能力和运算求解能力,正确利用面面垂直的性质定理求出棱锥的高是解决本题的关键.计算失误是失分的主要原因.
【三年模拟】
一、选择题(每小题5分,共10分)
1.(2019届吉林长春质监一,8)在正方体ABCD-A1B1C1D1中,直线A1C1与平面ABC1D1所成角的正弦值为( )
A.1 B.32 C.22 D.12
答案 D
2.(2018湖南衡阳3月模拟,7)设α、β是空间两个平面,m、n、l是空间三条直线,则下列四个命题中,逆命题成立的个数是( )
①当n⊂α时,若n⊥β,则α⊥β
②当l⊥α时,若l⊥β,则α∥β
③当n⊂α,且l⊄α时,若l∥α,则n∥l
④当n⊂α,且l是m在α内的射影时,若n⊥l,则m⊥n.
A.1 B.2 C.3 D.4
答案 C
二、填空题(共5分)
3.(2018广东七校3月联考,15)如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,下列结论中能成立的序号为 .
①ED⊥平面ACD;②CD⊥平面BED;③BD⊥平面ACD;④AD⊥平面BED.
答案 ④
三、解答题(共85分)
4.(2019届河北衡水中学第一次摸底,18)在△ABC中,D,E分别为AB,AC的中点,AB=2BC=2CD,如图1.以DE为折痕将△ADE折起,使点A到达点P的位置,如图2.
(1)证明:平面BCP⊥平面CEP;
(2)若平面DEP⊥平面BCED,求直线DP与平面BCP所成角的正弦值.
解析 (1)证明:在题图1中,AB=2BC=2CD,
且D为AB的中点,由平面几何知识,得∠ACB=90°.
因为E为AC的中点,所以DE∥BC.
在题图2中,CE⊥DE,PE⊥DE,且CE∩PE=E,
所以DE⊥平面CEP,所以BC⊥平面CEP.
又因为BC⊂平面BCP,所以平面BCP⊥平面CEP.
(2)因为平面DEP⊥平面BCED,平面DEP∩平面BCED=DE,EP⊂平面DEP,EP⊥DE,
所以EP⊥平面BCED.
又因为CE⊂平面BCED,所以EP⊥CE.
以E为坐标原点,分别以ED,EC,EP的方向为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系.
在题图1中,设BC=2a,则AB=4a,AC=23a,AE=CE=3a,DE=a.
则P(0,0,3a),D(a,0,0),C(0,3a,0),B(2a,3a,0).
所以DP=(-a,0,3a),BC=(-2a,0,0),CP=(0,-3a,3a).
设n=(x,y,z)为平面BCP的法向量,
则n·BC=0,n·CP=0,即-2ax=0,-3ay+3az=0.
令y=1,则z=1,所以n=(0,1,1).
设DP与平面BCP所成的角为θ,
则sin θ=|cos|=|n·DP||n||DP|=3a2×2a=64.
所以直线DP与平面BCP所成角的正弦值为64.
方法总结 在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直,或者可以通过建系的方法求两个平面的法向量,使得两个面的法向量互相垂直即可.
5.(2019届重庆第一中学10月月考,18)如图,三棱柱ABC-A1B1C1中,A1C⊥B1A1,AB=AA1,∠BAA1=60°.
(1)求证:AC=BC;
(2)若平面ABC⊥平面ABB1A1,且AB=BC,求二面角A1-CC1-B的正弦值.
解析 (1)证明:如图,取AB的中点D,连接CD,A1D,设AB=2,则AD=12AB=1,
又∵∠BAA1=60°,∴AB⊥DA1.∵CA1⊥A1B1,AB∥A1B1,∴CA1⊥AB,又∵CA1∩DA1=A1,∴AB⊥平面CDA1.∵CD⊂平面CDA1,∴AB⊥CD,在△ABC中,由三线合一可得AC=BC.
(2)因为平面ABC⊥平面ABB1A1,平面ABC∩平面ABB1A1=AB,且AB⊥CD,所以CD⊥平面AA1B1B.如图,建立空间直角坐标系,
则D(0,0,0),A1(0,3,0),C(0,0,3),B(-1,0,0),C1(-1,3,3),故CA1=(0,3,-3),CC1=(-1,3,0),CB=(-1,0,-3),
设平面A1CC1的法向量为n1=(x1,y1,z1),
则3y1-3z1=0,-x1+3y1=0⇒n1=(3,1,1),同理,平面BCC1的一个法向量为n2=(3,1,-1),设所求二面角为θ,则|cos θ|=|n1·n2||n1||n2|=35,sin θ=45.
所以二面角A1-CC1-B的正弦值为45.
6.(2019届广东化州一模,19)已知长方形ABCD中,AB=1,AD=2,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
(1)试问:在折叠的过程中,异面直线AB与CD能否垂直?若能垂直,求出相应的a的值;若不垂直,请说明理由;
(2)当四面体A-BCD体积最大时,求二面角A-CD-B的余弦值.
解析 (1)能垂直.若AB⊥CD,因为AB⊥AD,AD∩CD=D,所以AB⊥平面ACD⇒AB⊥AC.
由于AB=1,AD=BC=2,AC=a,所以AB2+a2=BC2,所以12+a2=(2)2⇒a=1,所以在折叠的过程中,异面直线AB与CD可以垂直,此时a的值为1.
(2)要使四面体A-BCD体积最大,因为△BCD面积为定值22,
所以只需三棱锥A-BCD的高最大即可,此时平面ABD⊥平面BCD.过A作AO⊥BD于O,则AO⊥平面BCD,以O为原点建立空间直角坐标系O-xyz(如图),
则A0,0,63,C63,33,0,D0,233,0,显然,平面BCD的一个法向量为OA=0,0,63,设平面ACD的法向量为n=(x,y,z),因为CD=-63,33,0,DA=0,-233,63,所以6x=3y,23y=6z,令y=2,得n=(1,2,2),∴cos=OA·n|OA|·|n|=26363×1+2+4=277.结合图形知,二面角A-CD-B为锐角,故二面角A-CD-B的余弦值为277.
解后反思 传统方法求线面角和二面角,一般有“一作,二证、三求”三个步骤.首先根据二面角的定义结合几何体中的线面关系作出线面角或二面角的平面角,进而求出;而角的计算大多采用建立空间直角坐标系,写出向量的坐标,利用线面角和二面角公式,借助法向量求空间角.
7.(2018安徽江淮十校4月联考,18)四棱锥A-BCDE中,EB∥DC,且EB⊥平面ABC,EB=1,DC=BC=AB=AC=2,F是棱AD的中点.
(1)证明:EF⊥平面ACD;
(2)求二面角B-AE-D的余弦值.
解析 (1)证明:取AC的中点M,连接FM、BM,
∵F是AD的中点,∴FM∥DC,且FM=12DC=1.
又∵EB∥DC,EB=1,∴FM