2021届课标版高考理科数学大一轮复习课件：2-7　函数与方程（讲解部分）

2021届课标版高考理科数学大一轮复习课件：2-7　函数与方程（讲解部分）

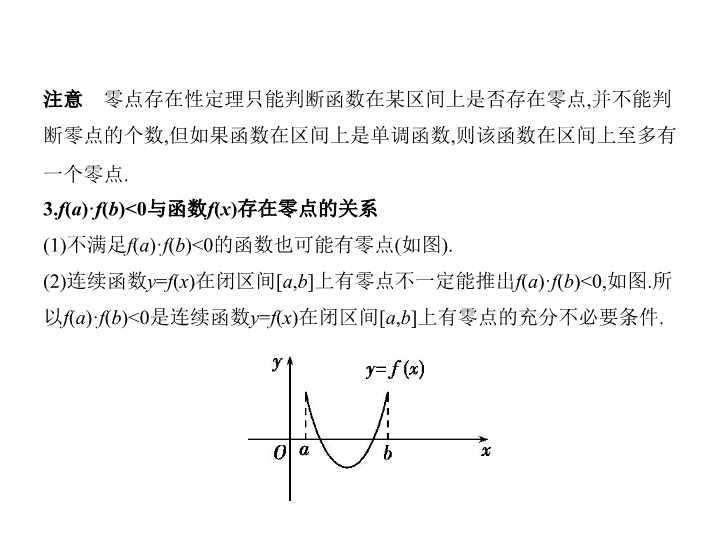
考点    函数的零点与方程的根 考点清单 考向基础 1.函数的零点 (1)函数零点的定义:对于函数 y = f ( x ),把使 f ( x )=0 的实数 x 叫做函数 y = f ( x )的零点. (2)三个等价关系:方程 f ( x )=0有实数根 ⇔ 函数 y = f ( x )的图象与 x 轴 有交点 ⇔ 函数 y = f ( x )有 零点 . 2.函数零点存在性定理   注意 　零点存在性定理只能判断函数在某区间上是否存在零点,并不能判 断零点的个数,但如果函数在区间上是单调函数,则该函数在区间上至多有 一个零点. 3. f ( a )· f ( b )<0与函数 f ( x )存在零点的关系 (1)不满足 f ( a )· f ( b )<0的函数也可能有零点(如图). (2)连续函数 y = f ( x )在闭区间[ a , b ]上有零点不一定能推出 f ( a )· f ( b )<0,如图.所 以 f ( a )· f ( b )<0是连续函数 y = f ( x )在闭区间[ a , b ]上有零点的充分不必要条件.   4.二分法 (1)对于区间[ a , b ]上连续不断的,且 f ( a )· f ( b )<0的函数 y = f ( x ),通过不断地把函 数 f ( x )的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,从而 得到零点近似值的方法,叫做二分法. (2)用二分法求函数 f ( x )零点近似值的步骤 第一步,确定区间[ a , b ],验证 f ( a )· f ( b )<0,给定精确度ε. 第二步,求区间( a , b )的中点 x 1 . 第三步,计算 f ( x 1 ): (i)若 f ( x 1 )=0,则 x 1 就是函数的零点; (ii)若 f ( a )· f ( x 1 )<0,则令 b = x 1 (此时零点 x 0 ∈( a , x 1 )); (iii)若 f ( x 1 )· f ( b )<0,则令 a = x 1 (此时零点 x 0 ∈( x 1 , b )). 第四步,判断是否达到精确度ε,即若| a - b |<ε,则得到零点近似值 a (或 b );否则, 重复第二、三、四步. 考向突破 考向一    确定函数零点所在区间 例1     (2019重庆南开中学3月模拟,4)函数 f ( x )=ln x +2 x -6的零点一定位于区 间   (　　) A.(1,2)内　　　　    B.(2,3)内　　　　    C.(3,4)内　　　　    D.(4,5)内 解析 　函数 f ( x )=ln x +2 x -6在其定义域上连续, f (2)=ln 2+2 × 2-6=ln 2-2<0, f (3)=ln 3+2 × 3-6=ln 3>0. 故函数 f ( x )=ln x +2 x -6的零点在区间(2,3)内,故选B. 答案     B 考向二    函数零点的应用 例2     (2019江西吉安一中、九江一中、新余一中等八所重点中学4月联 考,8)已知 f ( x )=   若关于 x 的方程 a = f ( x )恰有两个不同实根,则 实数 a 的取值范围是   (　　) A.   ∪ [1,2)　　　　    B.   ∪ [1,2) C.(1,2)　　　　    D.[1,2) 解析 　关于 x 的方程 a = f ( x )恰有两个不同实根等价于直线 y = a 、 y = f ( x )的图 象有两个不同的交点,画出直线 y = a 、 y = f ( x )的图象,如图,由图可知,当 a ∈   ∪ [1,2)时,直线 y = a 、 y = f ( x )的图象有两个不同的交点,此时,关于 x 的方 程 a = f ( x )恰有两个不同实根,所以实数 a 的取值范围是   ∪ [1,2).故选B.   答案     B 方法1      判断函数零点所在区间和零点的个数 1.判断函数零点所在区间的常用方法 (1)零点存在性定理,使用条件是函数图象是连续的. (2)数形结合法:画出函数的图象,估算确定区间. 2.判断函数零点个数的常用方法 (1)解方程法:令 f ( x )=0,如果有解,则有几个解就有几个零点. (2)函数零点存在性定理:利用该定理不仅要求函数图象在[ a , b ]上的图象是 连续的曲线,且 f ( a )· f ( b )<0,还必须结合函数的图象和性质(如单调性、奇偶 性、周期性、对称性)才能确定函数有多少个零点. (3)数形结合法:转化为两个函数图象的交点的个数问题,有几个交点就有 几个不同的零点. 方法技巧 例1　 (1)(2019河南百校联盟考前仿真,10)已知单调函数 f ( x )的定义域为(0, + ∞ ),对于定义域内任意 x , f [ f ( x )-log 2 x ]=3,则函数 g ( x )= f ( x )+ x -7的零点所在的 区间为   (　　) A.(1,2)　　　　    B.(2,3)　　　　    C.(3,4)　　　　    D.(4,5) (2)函数 f ( x )=2 x |log 0.5 x |-1的零点个数为   (　　) A.1　　　　    B.2　　　　    C.3　　　　    D.4 解析　 (1)根据题意,对任意的 x ∈(0,+ ∞ ),都有 f [ f ( x )-log 2 x ]=3, f ( x )是定义在 (0,+ ∞ )上的单调函数,则 f ( x )-log 2 x 为定值,设 t = f ( x )-log 2 x ,则 f ( x )=log 2 x + t ,又由 f ( t )=3,所以 f ( t )=log 2 t + t =3,所以 t =2,所以 f ( x )=log 2 x +2,所以 g ( x )=log 2 x + x -5,因为 g (1)<0, g (2)<0, g (3)<0, g (4)>0, g (5)>0,所以零点所在的区间为(3,4). (2)函数 f ( x )=2 x |log 0.5 x |-1的零点个数即为方程|log 0.5 x |=   =   的根的个数, 亦即函数 y 1 =|log 0.5 x |与 y 2 =   的图象的交点个数.两个函数的图象如图所 示,可知两个函数图象有两个交点,故选B. 答案 　(1)C　(2)B 方法2      已知函数有零点(方程有根)求参数值(取值范围)常用的方法 1.直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; 2.分离参数法:先将参数分离,转化成求函数的值域问题加以解决; 3.数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图 象,然后数形结合求解. 例2 　直线 y = x 与函数 f ( x )=   的图象恰有三个公共点,则实数 m 的取值范围是 　　　　　　     . 解析 　根据题意,知直线 y = x 与 y =2( x > m )的图象有一个交点 A (2,2),并且与抛 物线 y = x 2 +4 x +2在(- ∞ , m ]上的部分有两个交点 B 、 C , 由   解得 B (-1,-1), C (-2,-2), ∵抛物线 y = x 2 +4 x +2在(- ∞ , m ]上的部分必须包含 B 、 C 两点,且点 A (2,2)一定 在 y =2( x > m )的图象上,才能使 y = f ( x )的图象与直线 y = x 有3个交点, ∴实数 m 的取值范围是-1 ≤ m <2.   答案 　-1 ≤ m <2