湖北省2020届高三数学理一轮复习典型题专项训练：三角函数

湖北省2020届高三数学理一轮复习典型题专项训练：三角函数

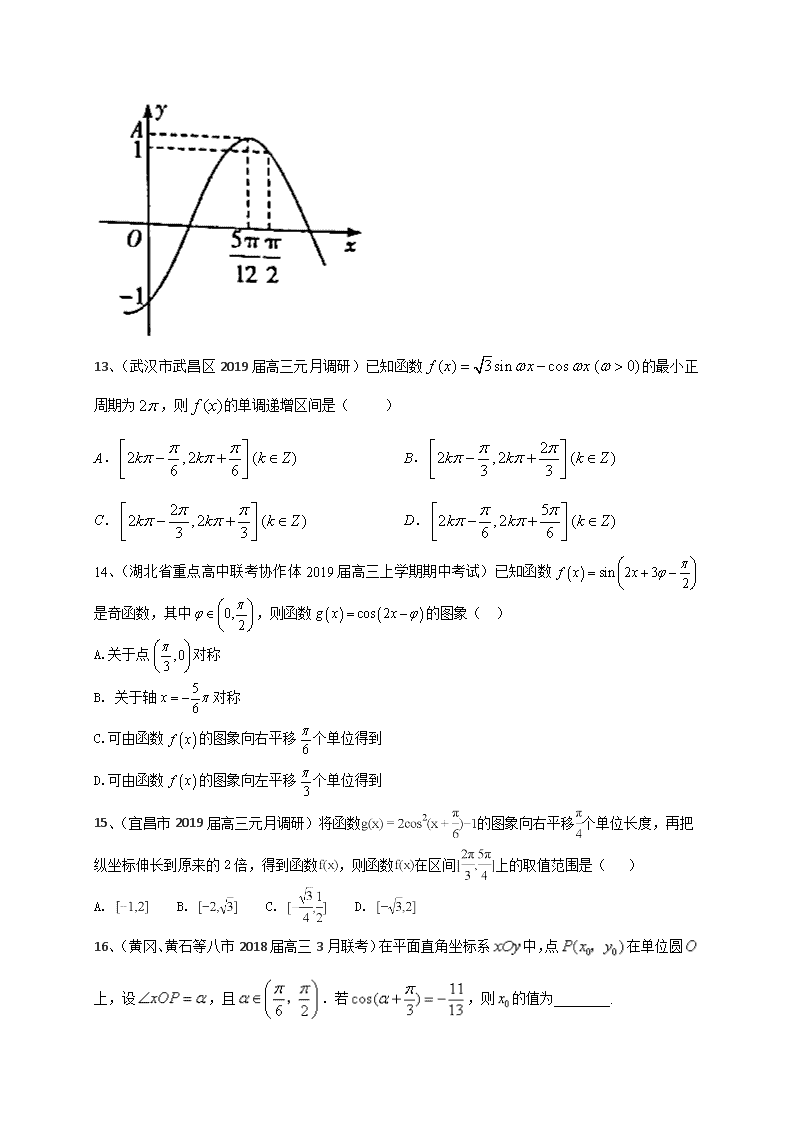
湖北省2020届高三数学理一轮复习典型题专项训练 三角函数 一、选择、填空题 ‎1、（荆、荆、襄、宜四地七校考试联盟2019届高三2月月考）已知函数在区间上是增函数,且在区间上存在唯一的使得,则的取值不可能为（ ）‎ A. B. C. D. ‎ ‎2、（鄂州市2019届高三上学期期中考试）计算的结果是（　 ）‎ A. B. C. D.‎ ‎3、（华中师范大学第一附属中学2019届高三5月押题考）设函数，将函数的图像向左平移 (>0)个单位长度，得到函数的图像，若为偶函数，则的最小值是 A. B. C. D. ‎ ‎4、（黄冈、黄石等八市2019届高三3月联考）在△ABC中，角A，B，C的对边分别为a，b，c，若a＝2，c=3，，则△ABC的面积为 ‎ A. 2 　　B. ‎3 ‎　　C.3　　　D.4‎ ‎5、（黄冈中学、华师一附中等八校2019届高三第二次（3月）联考）函数的最大值为 A. B.1 C.2 D.‎ ‎6、（黄冈中学、华师一附中等八校2019届高三第一次（12月）联考）已知同时满足下列三个条件：‎ ‎①时最小值为，②是奇函数，③.‎ 若在上没有最大值，则实数的范围是（ ）‎ A． B． C． D．‎ ‎7、（荆门市2019届高三元月调研）若将函数的图象向右平移个单位长度，得到函数的图象，且的图象关于原点对称，则的最小值为 A． B． C． D．‎ ‎8、（荆州市2019届高三上学期质量检查（一））已知的面积为1，角，，的对边分别为，，，且，，则角的大小为（ ）‎ A． B． C. D．‎ ‎9、（七市（州）教研协作体2019届高三3月联考）函数在[0，p ]内的值域为[－1，]， 则w 的取值范围是 　▲　 ．‎ ‎10、（武汉市2019届高中毕业生二月调研）已知函数在区间上单调递增，则的最大值为（ ）‎ A． B．1 C．2 D．4‎ ‎11、（武汉市2019届高中毕业生四月调研）为了得到函数y＝sin2x的图象，可以将的图象 A.向右平移个单位长度 B.向右平移个单位长度 C.向左平移个单位长度 D.向左平移个单位长度 ‎12、（武汉市2019届高中毕业生五月训练题）函数f（x）＝Asin（ωx﹣φ），其部分图象如图所示，则f（x）的表达式是（　　）‎ A． B． ‎ C． D．‎ ‎13、（武汉市武昌区2019届高三元月调研）已知函数的最小正周期为，则的单调递增区间是（ ）‎ A． B．‎ C． D．‎ ‎14、（湖北省重点高中联考协作体2019届高三上学期期中考试）已知函数是奇函数，其中，则函数的图象（ ）‎ A.关于点对称 B. 关于轴对称 C.可由函数的图象向右平移个单位得到 D.可由函数的图象向左平移个单位得到 ‎15、（宜昌市2019届高三元月调研）将函数的图象向右平移个单位长度，再把纵坐标伸长到原来的2倍，得到函数，则函数在区间上的取值范围是（ ）‎ A. B. C. D. ‎ ‎16、（黄冈、黄石等八市2018届高三3月联考）在平面直角坐标系中，点在单位圆上，设，且．若，则的值为________.‎ ‎17、（黄冈中学2018届高三5月二模）在中，角所对的边分别为，已知，，则的面积的最大值为 ．‎ ‎18、（荆州市2018届高三第一次质量检查）已知角α的终边经过点P(-5，-12)，则的值等于 ‎ A． B． C． D．‎ 参考答案：‎ ‎1、A 2、B 3、A 4、B 5、C ‎6、D 7、A 8、C 9、 10、C ‎11、A 12、B 13、B 14、A 15、D ‎16、　　　‎ ‎17、【答案】 ，，整理得 ‎，则 又，.又，则, ，， ‎ ‎，当且仅当时取等号.‎ ‎18、C　‎ 二、解答题 ‎1、（荆、荆、襄、宜四地七校考试联盟2019届高三2月月考）如图, 四点共圆,为钝角且, ‎ ‎,,‎ ‎（1）求;‎ ‎（2）设,,求的值.‎ ‎2、（鄂州市2019届高三上学期期中考试）在中，角所对的边分别为，且.‎ ‎（Ⅰ）证明：成等比数列；‎ ‎（Ⅱ）若，且，求的周长.‎ ‎3、（华中师范大学第一附属中学2019届高三5月押题考）在△ABC中，，AD是∠BAC的内角平分线，点D在线段BC上，且BD=2CD.‎ ‎(1)求sinB的值；‎ ‎(2)若AD=1，求△ABC的面积.‎ ‎4、（黄冈中学、华师一附中等八校2019届高三第一次（12月）联考）在中，已知点在边上，且，，.‎ ‎（1）若，求的值；‎ ‎（2）若，求边上的中线的长. ‎ ‎5、（荆门市2019届高三元月调研）在中，角、、所对的边分别为、、，且．‎ ‎（Ⅰ）求角的值；‎ ‎（Ⅱ）若的面积为，且，求的周长．‎ ‎6、（荆州市2019届高三上学期质量检查（一））已知函数，.‎ ‎（1）求函数的最小值，并写出取得最小值时的集合；‎ ‎（2）将函数的图象向右平移个单位长度，得到函数的图象，求函数的单调递增区间。‎ ‎7、（七市（州）教研协作体2019届高三3月联考）在锐角 DABC 中， 角 A，B，C 的对边分别为 a，b，c ， 且 ‎ ‎（ 1） 求角 B 的大小；‎ ‎（ 2） 若b = 2，求 a + c 的取值范围.‎ ‎8、（武汉市2019届高中毕业生二月调研）在中，角的对边分别为．已知．‎ ‎（1）求；‎ ‎（2）求的面积．‎ ‎9、（武汉市2019届高中毕业生四月调研）在中，角，，的对边分别为，，，若，，.‎ ‎(1)求；‎ ‎(2)已知在边上，且，求的面积.‎ ‎10、（武汉市2019届高中毕业生五月训练题）如图，在△ABC中，BC＝4，AC＝5，AB＝6，D在边AB上，CD为△ABC的角平分线．‎ ‎（1）求CD的长；‎ ‎（2）求△ACD的面积．‎ ‎11、（武汉市武昌区2019届高三元月调研）在中，角的对边分别为，且 ‎，‎ ‎．‎ ‎（1）求和的大小；‎ ‎（2）若的面积为，求边上中线的长．‎ ‎12、（湖北省重点高中联考协作体2019届高三上学期期中考试）的内角的对边分别为，且.‎ ‎（1）求；‎ ‎（2）若，求的面积.‎ ‎13、（宜昌市2019届高三元月调研）已知、、是的内角、、所对的边，的面积为，，且.‎ ‎（1）求的值；‎ ‎（2）若点为边上一点，且，求的长.‎ ‎14、（黄冈市2018届高三上学期期末考试）在锐角△ABC中，D为BC边的中点，且AC=,AD=,0为△ABC外接圆的圆心，且cos∠BOC= - .‎ ‎(1)求sin∠BAC的值;‎ ‎ (2)求△ABC的面积. ‎ ‎15、（荆州市2018届高三第一次质量检查）已知函数．‎ ‎ （1）若f(x)＝0，，求x的值；‎ ‎ （2）将函数f(x)的图象向左平移 个单位，再将图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），得到函数g(x)的图象，若曲线y＝h(x)与y＝g(x)的图象关于直线对称，求函数h(x)在上的值域．‎ 参考答案：‎ ‎1、解：（1），且角为钝角，.‎ 在中，由余弦定理得，，‎ ‎，解得或（舍），‎ ‎. …………6分 ‎（2）连接AC，则与互补，于是 在中由正弦定理…………12分 其它方法酌情给分.‎ ‎2、（1）证明：由正弦定理得：…………………2分 ‎，…………………………………………………4分 所以成等比数列………………………………………………………………6分 （1） 由…8分 由余弦定理得：，………………………………………………………9分 又，所以………………………………………………………………………10分 于是得：…………………………………………11分 所以的周长为.………………………………………………………………12分 ‎3、‎ ‎4、(1) ‎ ‎. ………………6分 ‎（2） ∵∴‎ ‎………………8分 又，所以 ………………12分 ‎5、解：（Ⅰ）由正弦定理：，又由已知，‎ 所以，………………………………………………………………………3分 ‎， 因为，所以．…………………………………………6分 ‎（Ⅱ）由正弦定理得，，则，‎ 中，由余弦定理，，‎ 则……………………………………………………………………………10分 故，‎ 所以的周长为．…………………………………………12分 ‎6、解：（1）‎ 令，得 故取最小值时的集合为 ‎（2）‎ 令，解得 所以的单调增区间为，‎ ‎7、‎ ‎8、解析：（1）由，知，‎ ‎，而，，‎ 即，而．…………………………………6分 ‎（2）在中，由余弦定理得：，‎ 所以的面积．………………………………12分 解法2：，由海伦公式得：‎ 的面积．……………………12分 ‎9、【解答】解析1：‎ ‎(1)由，，知，‎ ‎ ‎ ‎ 由正弦定理可知 ‎(2)，‎ ‎ ，‎ ‎ 三角形的面积 ‎ 而 ‎ ‎ 解析2：‎ ‎(1)由得，‎ ‎(2)，‎ ‎ ，即 ‎ 解得：或，时，，（舍）‎ ‎ ，‎ ‎10、解：（1）∵在△ABC中，BC＝4，AC＝5，AB＝6，‎ ‎∴由余弦定理可得：cos∠ACB＝＝，‎ ‎∴sin∠ACB＝，‎ ‎∵CD为△ABC的角平分线，‎ ‎∴∠ACD＝∠BCD，‎ ‎∴1﹣2sin2∠ACD＝cos∠ACB＝，‎ ‎∴sin∠ACD＝，‎ ‎∵S△ABC＝S△ACD+S△BCD，即：＝+，‎ ‎∴解得CD＝…6分 ‎（2）由（1）可得：S△ACD＝＝＝．…12分 ‎11、解析：（1）因为，所以，‎ 所以，即，所以，‎ 因为，所以，即，‎ 因为，所以，‎ 即，所以． ……………………6分 ‎（2），因为，所以，‎ 在中，，‎ 所以．……………………………………………………………………………………12分 ‎12、解：（1）由已知得 由，得. ‎ ‎（2）由，得，，‎ 在中，‎ ‎，‎ 由正弦定理得，，‎ 所以 ‎.‎ ‎13、解：（1）∵，‎ ‎∴由正弦定理得，∴， ‎ 又∵， ‎ ‎∴，∴. ‎ ‎（2）设，则，‎ 由余弦定理得， ‎ 即，∴，∴.‎ ‎14、解:(1)由题设知∠BOC=2∠BAC,…………………………………1分 ‎∴cos∠BOC=cos2∠BAC=1-2sin2∠BAC= - …………………3分 ‎∴sin2∠BAC= ,sin∠BAC= .………………5分 ‎(2)延长AD至E,使AE=2AD,连接BE,CE,则四边形ABEC为平行四边形,∴CE=AB.…………6分 ‎ 在△ACE中,AE=2AD=,AC=,∠ACE=π-∠BAC,cos∠ACE=-cos∠BAC=- .……7分 ‎ ∴由余弦定理得,AE2=AC2+CE2-2AC·CE·cos∠ACE,‎ ‎ 即()2=()2+CE2-2×·CE×(-),‎ 解得CE=2,∴AB=CE=2, ………………………………………………9分 ‎∴S△ABC=AB·AC·sin∠BAC=×2××=.…………12分 ‎15、解：（2分）‎ ‎ （1）由，即，‎ ‎ 又，或0或。 （6分）‎ ‎（2）由题知， （8分）‎ 则= （10分）‎ ‎， 故函数的值域为（12分）‎