数学文卷·2018届新疆呼图壁县一中高三10月月考(2017
高三 10 月月考数学(文)试卷
一、选择题(每小题 5 分,共 60 分)
1、已知集合 , ,则( )
A. B. C. D. 的关系无法确定
2、已知 i 是虚数单位,则 =( )
A. B. C. D.
3、对抛物线 ,下列描述正确的是( )
A.开口向下,焦点为 B.开口向下,焦点为(0,-1)
C.开口向左,焦点为 D.开口向左,焦点为(-1,0)
4、已知平面向量 与 平行,则 的值是 ( )
A.-2 B.2 C. D.
5、“ ”是 的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
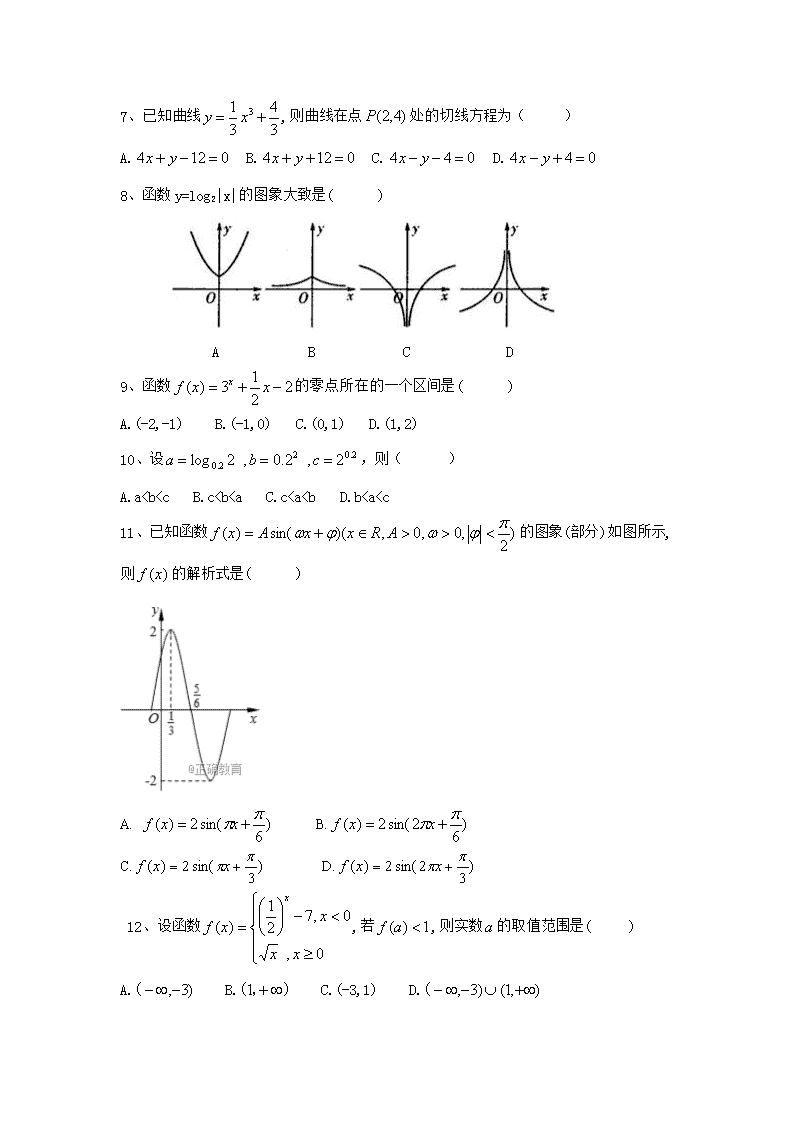
6、如图所示,程序框图(算法流程图)的输出结果是( )
A. B. C. D.
{ }21 <<−= xxA { }11 <<−= xxB
i
i
+
+
1
21
2
3 i−
2
3 i+
i-3 i+3
yx 42 −=
16
1-0,
016
1- ,
)3,( −= λa )2,3( −=b λ
2
9−
2
9
”“ 02 >+ xx
6
1
24
25
4
3
12
11
7、已知曲线 ,则曲线在点 处的切线方程为( )
A. B. C. D.
8、函数 y=log2|x|的图象大致是( )
A B C D
9、函数 的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
10、设 ,则( )
A.a
>∈+= ARxxAxf
)(xf
)6sin(2)(
ππ += xxf )62sin(2)(
ππ += xxf
)3sin(2)(
ππ += xxf )32sin(2)(
ππ += xxf
≥
<−
=
0,
0,72
1
)(
xx
xxf
x
1)( >=+ bab
y
a
xC 32
l NM , OM MN ON
次成等比数列,求 面积的取值范围.
22、(10 分)已知直线 (为参数),以坐标原点为极点,轴的正半轴为极轴
建立极坐标系,曲线 的极坐标方程为 .
(1)将曲线 C 的极坐标方程化为直角坐标方程;
(2)设点 的直角坐标为 ,直线 与曲线 的交点为 , ,求 的值.
OMN∆
+=
+=
ty
tx
l
2
13
2
35
:
θρ cos2=
M )( 3,5 l MBMA ⋅
高三 10 月月考数学(文)试卷答案
一、选择题
1—5 B B B D A 6—10 D C C C A 11—12 A C
二、填空题
13.3
14. -3
15. 1
16.
三、解答题
17.答案: (1)设等差数列 的公差为 ,
∵ , ,∴ ,即 .
∴ ∴ .
(2) .
18. 答案: 解析: (1)证明: 平面 , 平面 , .
为圆 O 的直径, ,
即 .又 = , 平面 .
平面 , .
(2)由题意,易得: ,从而
所以,平面 APC 与直线 PB 所成角 的余弦值
19.(文)f′(x)=-3x2+2ax+b,
因为函数 f(x)在 x=1 处的切线斜率为-3,
所以 f′(1)=-3+2a+b=-3,
( )212)23(2()1( −=−++++++ nnnnn
5,3 == PCBC 22=PB
θ
4
10cos =θ
又 f(1)=-1+a+b+c=-2 得 a+b+c=-1.
(1)函数 f(x)在 x=-2 时有极值,所以 f′(-2)=-12-4a+b=0
解得 a=-2,b=4,c=-3
所以 f(x)=-x3-2x2+4x-3.
(2)因为函数 f(x)在区间[-2,0]上单调递增,所以导函数 f′(x)=-3x2-bx+b 在区
间[-2,0]上的值恒大于或等于零,
则, ,解得 b≥4,
所以实数 b 的取值范围为[4+∞).
20.答案: (1)由已知得 , ,所以 , .
该超市所有顾客一次购物的结算时间组成一个总体,所收集的 位顾客一次购物的结
算时间可视为总体的一个容量为 的简单随机样本,顾客一次购物的结算时间的平均
值可用样本平均数估计,其估计值为
(分钟).
(2)记 为事件“一位顾客一次购物的结算时间不超过 分钟”, 分别表示
事件“该顾客一次购物的结算时间为 分钟”“该顾客一次购物的结算时间为 分
钟”“该顾客一次购物的结算时间为 分钟将频率视为概率得
.
因为 ,且 是彼此互斥事件,
所以
.
故一位顾客一次购物的结算时间不超过 分钟的概率为 .
21.解析: 试题分析:(1)由已知得 ∴ 方程:
≥′
≥−′
0)0(
0)2(
f
f
−=
=
=
222
322
2
bac
c
ba
(2)由题意可设直线 的方程为:
联立 消去 并整理,得:
则△ ,
此时设 、 ∴ ,
于是
又直线 、 、 的斜率依次成等比数列,
∴
由 得: .又由△ 得:
显然 (否则: ,则 中至少有一个为 0,直线 、 中至少有一
个斜率不存在,矛盾!)
设原点 到直线 的距离为 ,则
故由 得取值范围可得△ 面积的取值范围为
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。
本题求椭圆标准方程时,主要运用了椭圆的定义及几何性质。(2)作为研究点到直线的距
离最值问题,利用了函数思想。
22.答案: (1) 等价于 . ①
将 , 代入①,
即得曲线 的直角坐标方为 . ②
0)1(48)41( 222 =−+++ mkmxxk
221 41
8
k
kmxx +
−=+ 2
2
21 41
)1(4
k
mxx +
−=
2
2121
2
2121 )())(( mxxkmxxkmkxmkxyy +++=++=
2
21
2
2121
2
2
2
1
1 )( kxx
mxxkmxxk
x
y
x
y =+++=⋅
(2)将 代入②,
得 .
设这个方程的两个实根分别为 , ,
则由参数的几何意义即知, .