【数学】2020届一轮复习（文理合用）第7章第4讲直线、平面平行的判定与性质作业

【数学】2020届一轮复习（文理合用）第7章第4讲直线、平面平行的判定与性质作业

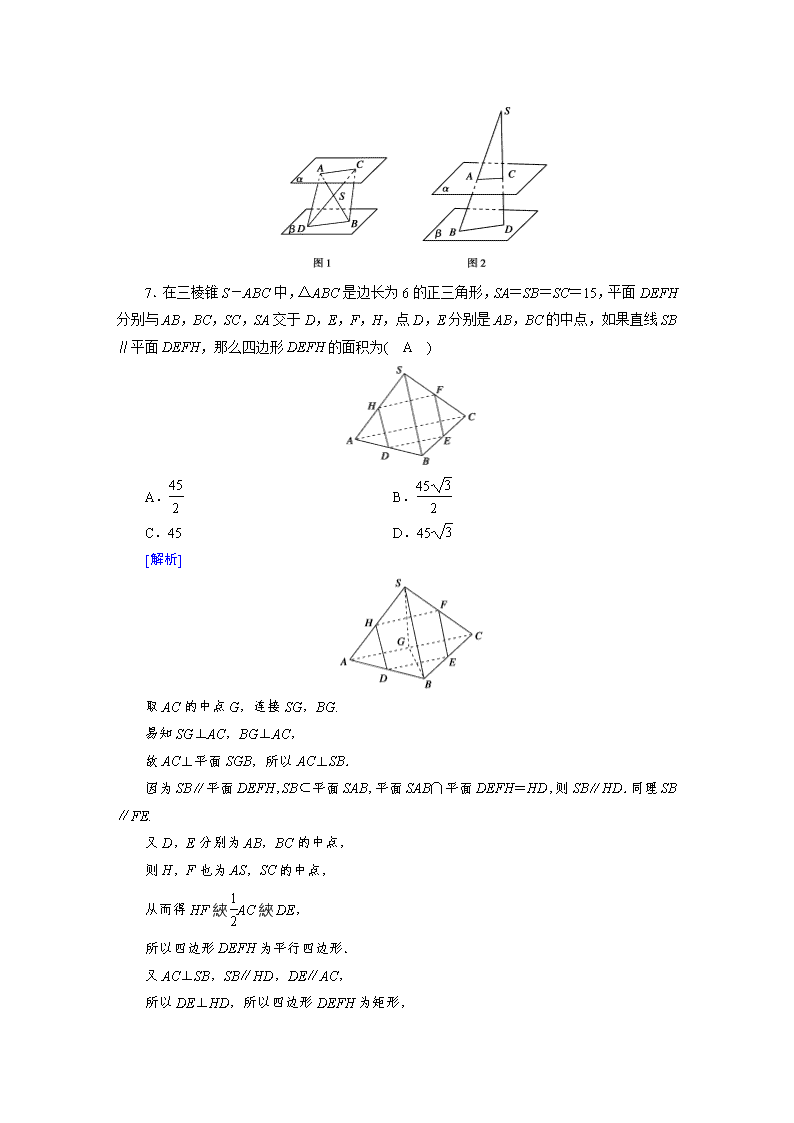
对应学生用书[练案49理][练案47文]‎ 第四讲　直线、平面平行的判定与性质 A组基础巩固 一、选择题 ‎1．(2019·山东泰安期末)有两条不同的直线m，n与两个不同的平面α，β，下列命题正确的是(　A　)‎ A．m⊥α，n∥β，且α∥β，则m⊥n B．m⊥α，n⊥β，且α⊥β，则m∥n C．m∥α，n⊥β，且α⊥β，则m∥n D．m∥α，n∥β，且α∥β，则m∥n ‎[解析]　对于A，由m⊥α，n∥β，且α∥β得m⊥n，故正确；对于B，由m⊥α，n⊥β，α⊥β得m⊥n，故错误；对于C，由m∥α，n⊥β，且α⊥β得m∥n或m，n相交或异面，故错误；对于D，由m∥α，n∥β，且α∥β得m，n的关系可以是相交或平行或异面，故错误．故选A．‎ ‎2．(2019·甘肃兰州诊断)已知直线m，n和平面α，则m∥n的一个必要条件是(　D　)‎ A．m∥α，n∥α　　　 B．m⊥α，n⊥α C．m∥α，，n⊂α　　　 D．m，n与平面α成等角 ‎[解析]　A中，m，n可以都和平面垂直，必要性不成立；B中，m，n可以都和平面平行，必要性不成立；C中，n不一定在平面内，必要性不成立；D中，m，n平行，则m，n与α成的角一定相等，但反之如果两直线m，n与α成的角相等则不一定平行，所以是必要不充分条件，故选D．‎ ‎3．(2019·青岛二模)已知m，n是两条不重合的直线，α，β，γ是三个不重合的平面，则α∥β的一个充分条件是(　D　)‎ A．m∥α，m∥β B．α⊥γ，β⊥γ C．m⊂α，n⊂β，m∥n D．m，n是异面直线，m⊂α，m∥β，n⊂β，n∥α ‎[解析]　A中，α，β可能相交，故错误；B不正确，如正方体中过同一个顶点的三个平面的关系；C中α，β可能相交，故错误；根据直线与平面平行的性质定理及平面与平面平行的判定定理可知D正确．‎ ‎4.在正方体ABCD－A1B1C1D1中，棱长为a，M、N分别为A1B和AC上的点，A1M＝AN＝，则MN与平面BB1C1C的位置关系是(　B　)‎ A．相交　　　 B．平行 C．垂直　　　 D．不能确定 ‎[解析]　连接CD1，在CD1上取点P，使D1P＝，∴MP∥BC，PN∥AD1.‎ ‎∴MP∥面BB1C1C，PN∥面AA1D1D．‎ ‎∴面MNP∥面BB1C1C，∴MN∥面BB1C1C．‎ ‎5.如图，P为平行四边形ABCD所在平面外一点，E为AD的中点，F为PC上一点，当PA∥平面EBF时，＝(　D　)‎ A．　　　　　 B． C．　　　　　 D． ‎[解析]　连接AC交BE于点G，连接FG，因为PA∥平面EBF，PA⊂平面PAC，平面PAC∩平面EBF＝FG，所以PA∥FG，所以＝.因为AD∥BC，AD＝BC，E为AD的中点，所以＝＝，所以＝.‎ ‎6．已知平面α∥β，点A，C∈α，B，D∈β，直线AB与直线CD交于点S，且AS＝8，BS＝9，CD＝34，则CS＝(　C　)‎ A．16　　　 B．18‎ C．16或272　　　 D．18或252‎ ‎[解析]　本题主要考查两平面平行的性质定理．①当点S在两平行平面之间时，如图1所示，∵直线AB与直线CD交于点S，直线AB与直线CD可确定一个平面γ，且α∩γ＝AC，β∩γ＝BD．∵α∥β，∴AC∥BD，∴＝，即＝，得＝，解得CS＝16.②当点S在两平行平面的同侧时，如图2所示，由①知AC∥BD，则有＝，即＝，解得CS＝272.故选C．‎ ‎7．在三棱锥S－ABC中，△ABC是边长为6的正三角形，SA＝SB＝SC＝15，平面DEFH 分别与AB，BC，SC，SA交于D，E，F，H，点D，E分别是AB，BC的中点，如果直线SB∥平面DEFH，那么四边形DEFH的面积为(　A　)‎ A．　　　 B．　　　‎ C．45　　　 D．45 ‎[解析]　‎ 取AC的中点G，连接SG，BG.‎ 易知SG⊥AC，BG⊥AC，‎ 故AC⊥平面SGB，所以AC⊥SB．‎ 因为SB∥平面DEFH，SB⊂平面SAB，平面SAB∩平面DEFH＝HD，则SB∥HD．同理SB∥FE.‎ 又D，E分别为AB，BC的中点，‎ 则H，F也为AS，SC的中点，‎ 从而得HF綊AC綊DE，‎ 所以四边形DEFH为平行四边形．‎ 又AC⊥SB，SB∥HD，DE∥AC，‎ 所以DE⊥HD，所以四边形DEFH为矩形，‎ 其面积S＝HF·HD＝(AD)·(SB)＝.‎ 二、填空题 ‎8．(2019·桂林二模)已知a，b，c为三条不重合的直线，α，β为两个不重合的平面，给出下列四个命题：①a∥b，b∥c⇒a∥c；②a∥α，b∥α⇒a∥b；③a∥α，β∥α⇒a∥β；④a⊄α，b⊂α，a∥b⇒a∥α.其中正确的命题是__①④___.(写出所有正确命题的序号)‎ ‎[解析]　根据线线平行的传递性，可知①正确；若a∥α，b∥α，则a，b可能平行、相交、异面，故②不正确；若a∥α，β∥α，则a∥β或a⊂β，故③不正确；由线面平行的判定定理可知④正确．故正确的命题是①④.‎ ‎9．正方体ABCD－A1B1C1D1的棱长为1 cm，过AC作平行于对角线BD1的截面，则截面面积为　 　cm2.‎ ‎[解析]　如图所示，截面ACE∥BD1，平面BDD1∩平面ACE＝EF，其中F为AC与BD的交点，‎ ‎∴E为DD1的中点，‎ ‎∴S△ACE＝××＝(cm2)．‎ ‎10．(2019·安徽安庆模拟)在正方体ABCD－A1B1C1D1中，M、N、Q分别是棱D1C1，A1D1、BC的中点，点P在BD1上且BP＝BD1.则下列四个说法：‎ ‎①MN∥平面APC；　　　　②C1Q∥平面APC；‎ ‎③A、P、M三点共线；　　　　④平面MNQ∥平面APC．‎ 其中说法正确的是__②③___.‎ ‎[解析]　①连接MN，AC，则MN∥AC，连接AM、CN，‎ 易得AM、CN交于点P，即MN⊂面APC，‎ 所以MN∥平面APC是错误的；‎ ‎②由①知M、N在平面APC内，由题易知AN∥C1Q，‎ 所以C1Q∥平面APC是正确的；‎ ‎③由①知，A，P，M三点共线是正确的；‎ ‎④由①知MN⊂平面APC，又MN⊂平面MNQ，‎ 所以平面MNQ∥平面APC是错误的．‎ 三、解答题 ‎11．如图所示，四边形ABCD与四边形ADEF都为平行四边形，M，N，G分别是AB，AD，EF的中点．求证：‎ ‎(1)BE∥平面DMF；‎ ‎(2)平面BDE∥平面MNG.‎ ‎[解析]　(1)如图所示，设DF与GN交于点O，连接AE，‎ 则AE必过点O，连接MO，则MO为△ABE的中位线，‎ 所以BE∥MO.‎ 因为BE⊄平面DMF，MO⊂平面DMF，‎ 所以BE∥平面DMF.‎ ‎(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN.‎ 因为DE⊄平面MNG，GN⊂平面MNG，‎ 所以DE∥平面MNG，‎ 因为M为AB的中点，所以MN为△ABD的中位线，‎ 所以BD∥MN.‎ 因为BD⊄平面MNG，MN⊂平面MNG，‎ 所以BG∥平面MNG.‎ 因为DE与BD为平面BDE内的两条相交直线，‎ 所以平面BDE∥平面MNG.‎ ‎12．(2019·福建泉州)在如图所示的多面体中，DE⊥平面ABCD，AF∥DE，AD∥BC，AB＝CD，∠ABC＝60°，BC＝2AD＝4DE＝4.‎ ‎(1)在AC上求作点P，使PE∥平面ABF，请写出作法并说明理由；‎ ‎(2)求三棱锥A－CDE的高．‎ ‎[解析]　(1)取BC的中点G，连接DG，交AC于P，连接PE.此时P为所求作的点．‎ 理由如下：‎ ‎∵BC＝2AD，∴BG＝AD，‎ 又BC∥AD，∴四边形BGDA是平行四边形，‎ 故DG∥AB，即DP∥AB．‎ 又AB⊂平面ABF，DP⊄平面ABF，∴DP∥平面ABF.‎ ‎∵AF∥DE，AF⊂平面ABF，DE⊄平面ABF，‎ ‎∴DE∥平面ABF.‎ 又∵DP⊂平面PDE，DE⊂平面PDE，PD∩DE＝D，∴平面ABF∥平面PDE，‎ 又∵PE⊂平面PDE，∴PE∥平面ABF.‎ ‎(2)在等腰梯形ABCD中，∵∠ABC＝60°，BC＝2AD＝4，‎ ‎∴可求得梯形的高为，从而△ACD的面积为×2×＝.‎ ‎∵DE⊥平面ABCD，∴DE是三棱锥E－ACD的高．‎ 设三棱锥A－CDE的高为h.‎ 由VA－CDE＝VE－ACD，可得S△CDE·h＝S△ACD·DE，‎ 即×2×1×h＝，解得h＝.‎ 故三棱锥A－CDE的高为.‎ B组能力提升 ‎1．有下列命题：‎ ‎①若直线l平行于平面α内的无数条直线，则l∥α；‎ ‎②若直线a在平面α外，则a∥α；‎ ‎③若直线a∥b，b∥α，则a∥α；‎ ‎④若直线a∥b，b∥α，则a平行于平面α内的无数条直线．‎ 其中真命题的个数是(　A　)‎ A．1　　　 B．2　　　‎ C．3　　　 D．4‎ ‎[解析]　命题①，l可以在平面α内，不正确；命题②，直线a与平面α可以是相交关系，不正确；命题③，a可以在平面α内，不正确；命题④正确．‎ ‎2.长方体ABCD－A1B1C1D1的底面ABCD是正方形，其侧面展开图是边长为8的正方形．E，F分别是侧棱AA1，CC1上的动点，AE＋CF＝8.P在棱AA1上，且AP＝2，若EF∥平面PBD，则CF＝__2___.‎ ‎[解析]　连接AC交BD于O，连接PO.‎ 因为EF∥平面PBD，EF⊂平面EACF，平面EACF∩平面PBD＝PO，‎ 所以EF∥PO，在PA1上截取PQ＝AP＝2，连接QC，则QC∥PO，所以EF∥QC，‎ 所以EFCQ为平行四边形，‎ 则CF＝EQ，又因为AE＋CF＝8，‎ AE＋A1E＝8.‎ 所以A1E＝CF＝EQ＝A1Q＝2，从而CF＝2.‎ ‎3．(2019·宜昌调研)如图，在棱长均相等的四棱锥P－ABCD中，O为底面正方形的中心，M，N分别为侧棱PA，PB的中点，有下列结论：‎ ‎①PC∥平面OMN；‎ ‎②平面PCD∥平面OMN；‎ ‎③OM⊥PA；‎ ‎④直线PD与MN所成角的大小为90°.‎ 其中正确结论的序号是__①②③___.(写出所有正确结论的序号)‎ ‎[解析]　如图，连接AC，易得PC∥OM，所以PC∥平面OMN，结论①正确．同理PD∥ON，所以平面PCD∥平面OMN，结论②正确．由于四棱锥的棱长均相等，所以AB2＋BC2＝PA2＋PC2＝AC2，所以PC⊥PA，又PC∥OM，所以OM⊥PA，结论③正确．由于M，N分别为侧棱PA，PB的中点，所以MN∥AB，又四边形ABCD为正方形，所以AB∥CD，又三角形PDC为等边三角形，所以∠PDC＝60°，所以直线PD与MN所成的角即∠PDC，故④错误．故正确的结论为①②③.‎ ‎4．如图所示，棱柱ABC－A1B1C1的侧面BCC1B1是矩形，D是A1C1上的动点，若A1B∥平面B1CD，则的值为　 　.‎ ‎[解析]　如图所示，在棱柱ABC－A1B1C1中，连接BC1交B1C于点E，连接DE，则DE是平面A1BC1与平面B1CD的交线．因为A1B∥平面B1CD，所以A1B∥DE.又E是BC1的中点，所以D是A1C1的中点，所以＝.‎ ‎5．(2019·衡中模拟)如图，在三棱柱ABC－DEF中，侧面ABED是边长为2的菱形，且∠ABE＝，BC＝.点F在平面ABED内的正投影为点G，且点G在AE上，FG＝，点M的线段CF上，且CM＝CF.‎ ‎(1)证明：直线GM∥平面DEF；‎ ‎(2)求三棱柱M－DEF的体积．‎ ‎[解析]　(1)证明：∵点F在平面ABED内的正投影为点G，‎ ‎∴FG⊥平面ABED，∴FG⊥GE，‎ 又BC＝＝EF，FG＝，∴GE＝.‎ ‎∵四边形ABED是边长为2的菱形，且∠ABE＝，‎ ‎∴AE＝2，∴AG＝.‎ 如图，过点G作GH∥AD交DE于点H，连接FH.‎ 则＝，∴GH＝，‎ 由CM＝CF得MF＝＝GH.‎ 又易证GH∥AD∥MF，‎ ‎∴四边形GHFM为平行四边形，∴MG∥FH.‎ 又GM⊄平面DEF，FH⊂平面DEF，‎ ‎∴GM∥平面DEF.‎ ‎(2)由(1)知GM∥平面DEF，连接GD，‎ 则有VM－DEF＝VG－DEF.‎ 又VG－DEF＝VF－DEG＝FG·S△DEG＝FG·S△DAE＝，‎ ‎∴VM－DEF＝.‎