2020届二轮复习高考审题答题四立体几何热点问题课件（23张）（全国通用）

2020届二轮复习高考审题答题四立体几何热点问题课件（23张）（全国通用）

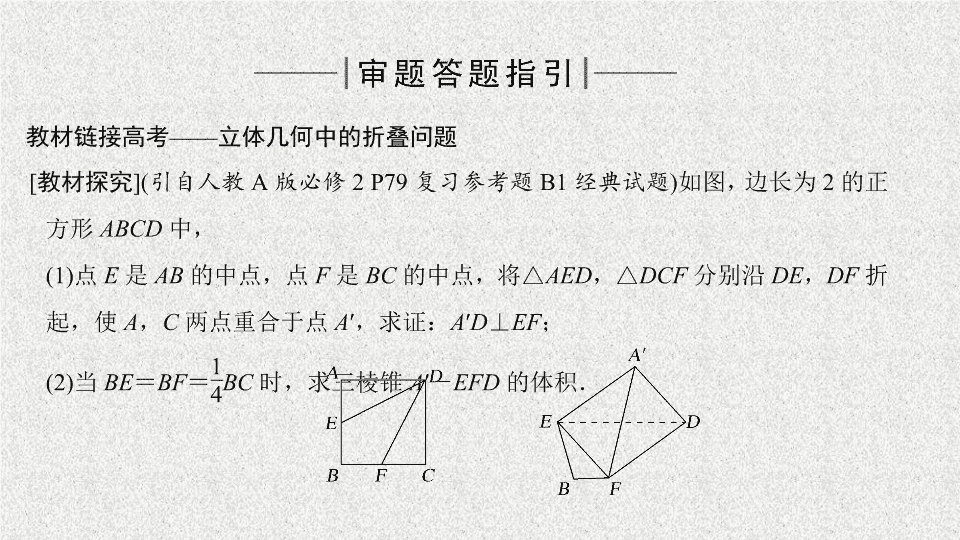
核心热点 真题印证 核心素养 平行关系的证明与体积或距离的计算 2017· Ⅱ ， 18 ； 2016· Ⅲ ， 19 ； 2017· 浙江， 19 ； 2016· 四川， 17 直观想象，逻辑推理，数学运算 垂直关系的证明与体积或距离的计算 2018· Ⅰ ， 18 ； 2018· Ⅱ ， 19 ； 2017· Ⅰ ， 18 ； 2017· Ⅲ ， 19 ； 2016· Ⅰ ， 18 ； 2016· Ⅱ ， 19 直观想象，逻辑推理，数学运算 平行与垂直关系的证明 2018· Ⅲ ， 19 ； 2017· 江苏， 15 ； 2018· 北京， 18 ； 2017· 北京， 18 直观想象，逻辑推理 教材链接高考 —— 立体几何中的折叠问题 [ 试题评析 ] 　 (1) 将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力． (2) 第 (1) 问要证明线线垂直，可通过证明线面垂直来完成，第 (2) 问求三棱锥的体积时，如果所给三棱锥的高不容易求出，可通过转换顶点法求解． (3) 答题时要注意第 (1) 、 (2) 问的条件是不同的，在第 (1) 问中 E ， F 分别是所在边的中点，而第 (2) 问中则不是，很多粗心的同学容易在这个地方出现失误． 证明 　由已知， AC ⊥ BC ，且 DE ∥ BC ，所以 DE ⊥ AC ， DE ⊥ DC ， DE ⊥ DA 1 ，因为 DC ∩ DA 1 ＝ D ， DC ， DA 1  平面 A 1 DC ，所以 DE ⊥ 平面 A 1 DC . 由于 A 1 F  平面 A 1 DC ，所以 DE ⊥ A 1 F ， 又 A 1 F ⊥ CD ， CD ∩ DE ＝ D ， CD ， DE  平面 BCDE ，所以 A 1 F ⊥ 平面 BCDE ， 而 BE  平面 BCDE ，所以 A 1 F ⊥ BE . 探究提高 　 解决折叠问题最重要的就是对比折叠前后的图形，找到哪些线、面的位置关系和数学量没有发生变化，哪些发生了变化，在证明和求解的过程中恰当地加以利用． 【链接高考】 (2018· 全国 Ⅰ 卷 ) 如图，在平行四边形 ABCM 中， AB ＝ AC ＝ 3 ， ∠ ACM ＝ 90°. 以 AC 为折痕将 △ ACM 折起，使点 M 到达点 D 的位置，且 AB ⊥ DA . (1) 证明　 由已知可得， ∠ BAC ＝ 90° ，即 BA ⊥ AC . 又 BA ⊥ AD ， AC ∩ AD ＝ A ， AC ， AD  平面 ACD ，所以 AB ⊥ 平面 ACD . 又 AB  平面 ABC ， 所以平面 ACD ⊥ 平面 ABC . (2) 解　 由已知可得， DC ＝ CM ＝ AB ＝ 3 ， 由已知及 (1) 可得 DC ⊥ 平面 ABC ，所以 QE ⊥ 平面 ABC ， QE ＝ 1. 因此，三棱锥 Q － ABP 的体积为 (1) 证明：平面 AMD ⊥ 平面 BMC ； (2) 在线段 AM 上是否存在点 P ，使得 MC ∥ 平面 PBD ？说明理由． [ 审题路线 ] [ 自主解答 ] (1) 证明　 由题设知，平面 CMD ⊥ 平面 ABCD ，交线为 CD . 因为 BC ⊥ CD ， BC  平面 ABCD ，所以 BC ⊥ 平面 CMD ，故 BC ⊥ DM . 所以 DM ⊥ CM . 又 BC ∩ CM ＝ C ， BC ， CM ⊂ 平面 BMC ，所以 DM ⊥ 平面 BMC . 而 DM  平面 AMD ，故平面 AMD ⊥ 平面 BMC . (2) 解　 当 P 为 AM 的中点时， MC ∥ 平面 PBD . 证明如下：如图，连接 AC 交 BD 于 O . 因为 ABCD 为矩形，所以 O 为 AC 中点．连接 OP ，因为 P 为 AM 中点，所以 MC ∥ OP . MC ⊄ 平面 PBD ， OP ⊂ 平面 PBD ，所以 MC ∥ 平面 PBD . 探究提高 　 1. 探索条件的常用方法： (1) 先猜后证，即先观察与尝试给出条件再证明； (2) 先通过命题成立的必要条件探索出命题成立的条件，再证明其充分性； (3) 把几何问题转化为代数问题，探索命题成立的条件． 2 ．探索结论的常用方法： 首先假设结论成立，然后在这个假设下进行推理论证，如果通过推理得到了合理的结论就肯定假设，如果得到了矛盾的结果就否定假设． 提醒 　开放问题把假设当作已知条件进行推理论证，会起到事半功倍之效． 【尝试训练】 如图，在三棱柱 ABC － A 1 B 1 C 1 中， A 1 A ⊥ 平面 ABC ， AC ⊥ BC ， E 在线段 B 1 C 1 上， B 1 E ＝ 3 EC 1 ， AC ＝ BC ＝ CC 1 ＝ 4. (1) 求证： BC ⊥ AC 1 ； (2) ( 一题多解 ) 试探究：在 AC 上是否存在点 F ，满足 EF ∥ 平面 A 1 ABB 1 ？若存在，请指出点 F 的位置，并给出证明；若不存在，请说明理由． 解 　 (1) 因为 AA 1 ⊥ 平面 ABC ， BC  平面 ABC ， 所以 BC ⊥ AA 1 . 又因为 BC ⊥ AC ， AA 1 ∩ AC ＝ A ， AA 1 ， AC  平面 AA 1 C 1 C ，所以 BC ⊥ 平面 AA 1 C 1 C ，又 AC 1  平面 AA 1 C 1 C ，所以 BC ⊥ AC 1 . (2) 法一 　当 AF ＝ 3 FC 时， EF ∥ 平面 A 1 ABB 1 . 证明如下： 如图，在平面 A 1 B 1 C 1 内过点 E 作 EG ∥ A 1 C 1 交 A 1 B 1 于点 G ，连接 AG . 因为 B 1 E ＝ 3 EC 1 所以 AF ∥ EG 且 AF ＝ EG ， 所以四边形 AFEG 为平行四边形， 所以 EF ∥ AG ，又 EF ⊄ 平面 A 1 ABB 1 ， AG  平面 A 1 ABB 1 ，所以 EF ∥ 平面 A 1 ABB 1 . 法二 　当 AF ＝ 3 FC 时， FE ∥ 平面 A 1 ABB 1 . 证明如下： 如图，在平面 BCC 1 B 1 内过点 E 作 EG ∥ BB 1 交 BC 于点 G ，连接 FG . 因为 EG ∥ BB 1 ， EG ⊄ 平面 A 1 ABB 1 ， BB 1  平面 A 1 ABB 1 ，所以 EG ∥ 平面 A 1 ABB 1 . 因为 B 1 E ＝ 3 EC 1 ，所以 BG ＝ 3 GC ， 所以 FG ∥ AB ， 又 AB  平面 A 1 ABB 1 ， FG  平面 A 1 ABB 1 ， 所以 FG ∥ 平面 A 1 ABB 1 . 又 EG  平面 EFG ， FG  平面 EFG ， EG ∩ FG ＝ G ， 所以平面 EFG ∥ 平面 A 1 ABB 1 . 又 EF  平面 EFG ， 所以 EF ∥ 平面 A 1 ABB 1 . 满分答题示范 —— 立体几何中的位置关系的证明 【例题】 (14 分 )(2018· 江苏卷 ) 在平行六面体 ABCD － A 1 B 1 C 1 D 1 中， AA 1 ＝ AB ， AB 1 ⊥ B 1 C 1 . 求证： (1) AB ∥ 平面 A 1 B 1 C ； (2) 平面 ABB 1 A 1 ⊥ 平面 A 1 BC . [ 规范解答 ] [ 高考状元满分心得 ] ❶ 得步骤分：抓住得分点的步骤， “ 步步为赢 ” ，求得满分．如第 (1) 问中证明线面平行时，应套用线面平行的判定定理的三个条件，不能漏掉 “ AB  平面 A 1 B 1 C ， A 1 B 1 ⊂ 平面 A 1 B 1 C ”  ．证明第 (2) 问中的线面垂直  和面面垂直  也是如此． ❷ 得关键分：解题过程中不可忽视关键点，有则给分，无则没分，如第 (2) 问中证明 AB 1 ⊥ A 1 B  和 AB 1 ⊥ BC  ． [ 构建模板 ] 求证： (1) 直线 EF ∥ 平面 PCD ； (2) 平面 BEF ⊥ 平面 PAD .