2018人教A版数学必修一1.1.1《集合的含义与表示》（第二课时）教案

2018人教A版数学必修一1.1.1《集合的含义与表示》（第二课时）教案

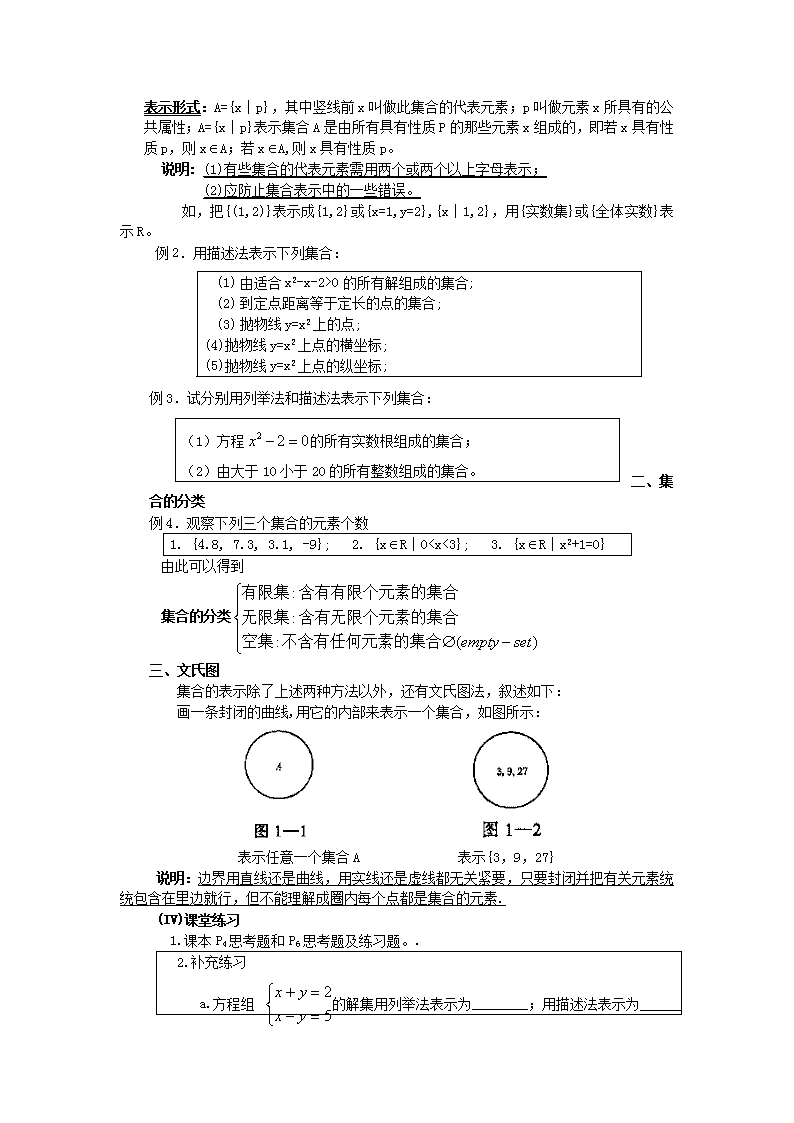
‎1.1.1‎‎ 集合的含义与表示（第二课时）‎ 教学目标：1.掌握集合的两种常用表示方法（列举法和描述法）。.‎ ‎2.通过实例能使学生选择自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题，感受集合语言的意义和作用。‎ 教学重点：集合的两种常用表示方法（列举法和描述法）‎ 教学难点：集合的两种常用表示方法（列举法和描述法）的理解 教学方法：尝试指导法和讨论法 教学过程：‎ ‎（I）复习回顾 问题1：集合元素的特征有哪些？怎样理解，试举例说明.‎ 问题2：集合与元素关系是什么？如何表示？‎ 问题3：常用的数集有哪些？如何表示？‎ ‎（II）引入问题 ‎ 问题4：在初中学正数和负数时，是如何表示正数集合和负数集合的? 如表示下列数中的正数 4.8,-3,,-0.5,,+73,3.1 ‎ ‎4.8,,+73,3.1, ‎ ‎ 方法1:‎ ‎ 方法2: {4.8,,,+73,3.1}‎ ‎ 问题5：在初中学习不等式时,如何表示不等式x+3<6的解集?（可表示为:x<3）‎ ‎(III) 讲授新课 ‎ 一、集合的表示方法 问题4中，方法1为图示法，方法2为列举法.‎ 1. 列举法：把集合中的元素一一列举出来,写在大括号里的方法.‎ 说明： (1)书写时，元素与元素之间用逗号分开；‎ ‎(2)一般不必考虑元素之间的顺序；‎ ‎(3)在表示数列之类的特殊集合时,通常仍按惯用的次序；‎ ‎(4)在列出集合中所有元素不方便或不可能时，可以列出该集合的一部分元素,以提供某种规律,其余元素以省略号代替；‎ 例1．用列举法表示下列集合：‎ (1) 小于5的正奇数组成的集合；‎ (2) 能被3整除而且大于4小于15的自然数组成的集合；‎ (3) 从51到100的所有整数的集合；‎ (4) 小于10的所有自然数组成的集合；‎ (5) 方程的所有实数根组成的集合；‎ (6) 由1~20以内的所有质数组成的集合。‎ ‎ 问题6：能否用列举法表示不等式x-7<3的解集? 由此引出描述法。‎ 2. 描述法：用集合所含元素的共同特征表示集合的方法(即把集合中元素的公共属性描述出来, 写在大括号里的方法)。‎ 表示形式：A={x∣p}，其中竖线前x叫做此集合的代表元素；p叫做元素x所具有的公共属性；A={x∣p}表示集合A是由所有具有性质P的那些元素x组成的，即若x具有性质p，则xA；若xA,则x具有性质p。‎ 说明: (1)有些集合的代表元素需用两个或两个以上字母表示；‎ ‎(2)应防止集合表示中的一些错误。‎ ‎ 如，把{(1,2)}表示成{1,2}或{x=1,y=2},{x∣1,2}，用{实数集}或{全体实数}表示R。‎ (1) 由适合x2-x-2>0的所有解组成的集合;‎ (2) 到定点距离等于定长的点的集合;‎ (3) 抛物线y=x2上的点;‎ ‎(4)抛物线y=x2上点的横坐标;‎ ‎(5)抛物线y=x2上点的纵坐标;‎ 例2．用描述法表示下列集合：‎ 例3．试分别用列举法和描述法表示下列集合：‎ ‎（1）方程的所有实数根组成的集合；‎ ‎（2）由大于10小于20的所有整数组成的集合。‎ ‎ ‎ 二、集合的分类 例4．观察下列三个集合的元素个数 ‎1. {4.8, 7.3, 3.1, -9}; 2. {xR∣0

查看更多