高中数学选修2-1公开课课件椭圆的第二定义
椭圆的第二定义
问题背景
首页
上页
下页
已知动点
M
到定点
(3
,
0)
的距离与到定直线
的距离之比等于 ,求动点
M
的轨迹。
问题
1
:
椭圆的焦点坐标和离心率分别是什么?
将上述问题一般化,你能得出什么猜想?
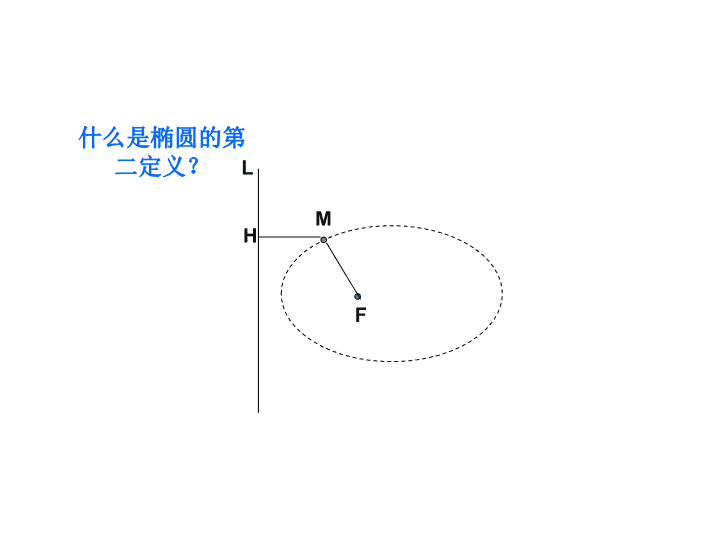
F
M
H
L
什么是椭圆的第二定义?
猜想证明
首页
上页
下页
点动点
M
(
x
,
y
)与定点
F
(
c
,
0
)的距离和它到定直线
L
:
的距离的比是常数
(0
c>0)
,求点
M
的轨迹。
证明:
回顾:求轨迹的一般步骤:
1.建系,设点.
2.列等式.
3.代入坐标得到方程.
4.化简方程.
5.证明(验证).
由此得
将上式两边平方并化简得
:
设
原方程可化为
:
解:
设
d
是点
M
到直线
的距离
,
依题意知,所求轨迹就
是集合
0
x
y
M
设
M
猜想证明
这是椭圆的标准方程
,
所以
M
点的轨迹是长轴长为
短轴长为
的椭圆
.
概念引入
问题
2
:
首页
上页
下页
(1)
定义中有哪些已知条件
?
(2)
定点定比在椭圆中的名称各是什么
?
(3)
定比的取值范围是什么
?
(4)
椭圆有几条准线
,
他们与椭圆的位置关系
?
由此可知
,
当点
M
与一个定点的距离和它到一条定直
线的距离的比是一个常数
时
,
这个点的
轨迹是椭圆
,
这叫做
椭圆的第二定义
,
定点是椭圆的
焦
点
,
定直线叫做椭圆的
准线
,
常数
e
是椭圆的
离心率
.
0
x
y
M
对于椭圆
相应
与焦点
的准线
方程是
由椭圆的对称性
,
相应
与焦点
的准线方程是
能不能说
M
到 的距离与到直线
的距离比也是离心率
e
呢
?
)
0
,
(
-c
F
¢
概念分析
练习1
:
求下列椭圆的焦点坐标和准线
(1)
y
2
__
36
+ =1
x
2
__
100
(2) 2x
2
+y
2
=8
焦点坐标
:(-8,0),(8,0).
准线方程
:
x=
±
25
__
2
焦点坐标
:(0,-2),(0,2).
准线方程
:
y=
±4
例题讲解
首页
上页
下页
例
2
:求中心在原点,一条准线方程是
x=3
,
离心率为 的椭圆标准方程。
解:
依题意设椭圆标准方程为
由已知有
解得
a=
c=
所求椭圆的标准方程为
例题讲解
首页
上页
下页
例
3.
椭圆方程为
,
其上有一点
P,
它到右焦点
的距离为
14,
求
P
点到左准线的距离
.
P
0
x
y
解
:
由椭圆的方程可知
:
由第一定义可知
:
由第二定义知
:
例题讲解
1.
椭圆第二定义是:
当点
M
与一个定点的距离和它到一条定
直线的距离的比是常数
e
= (0
>
=
+
b
a
b
x
a
y
达标训练
A
:
1
、椭圆 上一点到准线 与到焦点(
-2
,
0
)的距离
的比是 ( )
2
、椭圆 的准线平行于
x
轴,则
( )
(
A
)
0 〈 m<1/2 (B) m>1/2
且
m 1
(c) m<1/2
且
m 0 (D) m>0
且
m 1
3
、椭圆的两焦点把两准线间的距离三等分,则这个椭圆的离心率是
( )
B
C
C
4
、 (
1
)若椭圆 上一点
P
到右焦点
F
的距离为
3/2
,则
P
到左准线的
距离是
______________
(
2
)已知椭圆 上一点
P
到左准线的距离是
5/2
,则
P
到右焦点的
距离是
______________
、离心率
e=3/5,
一条准线的方程是
x=50/3
的椭圆的标准方程是
___________
B
1
、若椭圆 上一点到左准线的距离是到右准线的距离的
2
倍,则
这点的坐标是 ( )
8
A
2
、若椭圆 的焦点到相应准线的距离是
12
,则
m= ( )
(A)2 (B)6 (C)2
或
6 (D)12
3
、若椭圆 上有一点到右焦点的距离是
1
,则
P
点的
坐标是
____________
4
、若一个椭圆的离心率
e=1/2,
准线方程是
x=4,
对应的焦点
F
(
2
,
0
),
则椭圆的方程是
____________
C
(5,0)
3x
2
-8x+4y
2
=0