2019年高考数学高分突破复习练习专题六 第1讲

2019年高考数学高分突破复习练习专题六 第1讲

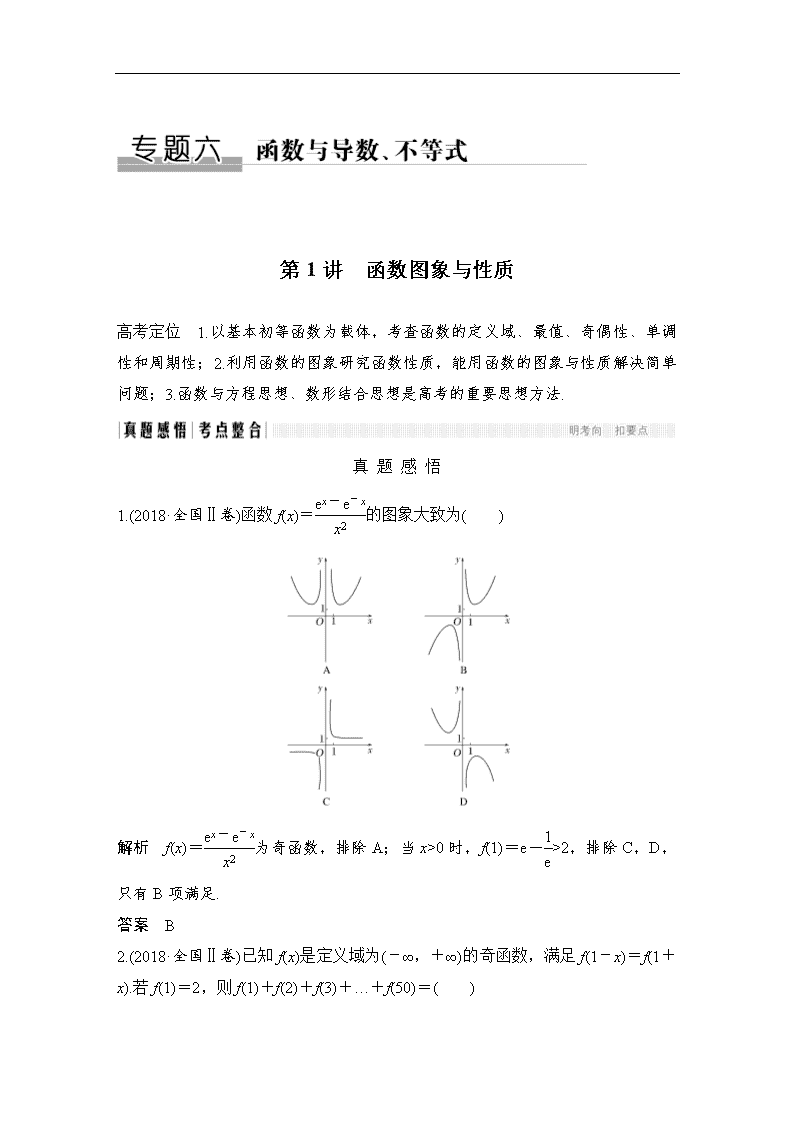
第1讲　函数图象与性质 高考定位　1.以基本初等函数为载体，考查函数的定义域、最值、奇偶性、单调性和周期性；2.利用函数的图象研究函数性质，能用函数的图象与性质解决简单问题；3.函数与方程思想、数形结合思想是高考的重要思想方法.‎ 真 题 感 悟 ‎1.(2018·全国Ⅱ卷)函数f(x)＝的图象大致为(　　)‎ 解析　f(x)＝为奇函数，排除A；当x>0时，f(1)＝e－>2，排除C，D，只有B项满足.‎ 答案　B ‎2.(2018·全国Ⅱ卷)已知f(x)是定义域为(－∞，＋∞)的奇函数，满足f(1－x)＝f(1＋x).若f(1)＝2，则f(1)＋f(2)＋f(3)＋…＋f(50)＝(　　)‎ A.－50 B.0 C.2 D.50‎ 解析　法一　∵f(x)是定义域为(－∞，＋∞)的奇函数，且f(1－x)＝f(1＋x)，∴f(4＋‎ x)＝f(x)，∴f(x)是周期函数，且一个周期为4，又f(0)＝0，知f(2)＝f(0)，f(4)＝f(0)＝0，由f(1)＝2，知f(－1)＝－2，则f(3)＝f(－1)＝－2，从而f(1)＋f(2)＋f(3)＋f(4)＝0，故f(1)＋f(2)＋f(3)＋f(4)＋…＋f(50)＝12×0＋f(49)＋f(50)＝f(1)＋f(2)＝2，故选C.‎ 法二　由题意可设 f(x)＝2sin，作出f(x)的部分图象如图所示.由图可知，f(x)的一个周期为4，所以f(1)＋f(2)＋f(3)＋…＋f(50)＝12[f(1)＋f(2)＋f(3)＋f(4)]＋f(49)＋f(50)＝12×0＋f(1)＋f(2)＝2.‎ 答案　C ‎3.(2017·全国Ⅰ卷)已知函数f(x)＝ln x＋ln(2－x)，则(　　)‎ A.f(x)在(0，2)上单调递增 B.f(x)在(0，2)上单调递减 C.y＝f(x)的图象关于直线x＝1对称 D.y＝f(x)的图象关于点(1，0)对称 解析　由题意知，f(x)＝ln x＋ln(2－x)的定义域为(0，2)，f(x)＝ln[x(2－x)]＝‎ ln[－(x－1)2＋1]，由复合函数的单调性知，函数f(x)在(0，1)上单调递增，在(1，2)上单调递减，所以排除A，B；又f(2－x)＝ln(2－x)＋ln x＝f(x)，所以f(x)的图象关于直线x＝1对称，C正确，D错误.‎ 答案　C ‎4.(2018·江苏卷)函数f(x)满足f(x＋4)＝f(x)(x∈R)，且在区间(－2，2]上，f(x)＝则f[f(15)]的值为________.‎ 解析　因为函数f(x)满足f(x＋4)＝f(x)(x∈R)，所以函数f(x)的最小正周期为4.又因为在区间(－2，2]上，f(x)＝ 所以f[f(15)]＝f[f(－1)]＝f ＝cos ＝.‎ 答案　 考 点 整 合 ‎1.函数的图象 ‎(1)对于函数的图象要会作图、识图和用图，作函数图象有两种基本方法：一是描点法；二是图象变换法，其中图象变换有平移变换、伸缩变换和对称变换.‎ ‎(2)在研究函数性质特别是单调性、值域、零点时，要注意结合其图象研究.‎ ‎(3)函数图象的对称性 ‎①若函数y＝f(x)满足f(a＋x)＝f(a－x)，即f(x)＝f(2a－x)，则y＝f(x)的图象关于直线x＝a对称；‎ ‎②若函数y＝f(x)满足f(a＋x)＝－f(a－x)，即f(x)＝－f(2a－x)，则y＝f(x)的图象关于点(a，0)对称.‎ ‎2.函数的性质 ‎(1)单调性：单调性是函数在其定义域上的局部性质.证明函数的单调性时，规范步骤为取值、作差、变形、判断符号和下结论.复合函数的单调性遵循“同增异减”的原则.‎ ‎(2)奇偶性：①若f(x)是偶函数，则f(x)＝f(－x).‎ ‎②若f(x)是奇函数，0在其定义域内，则f(0)＝0.‎ ‎③奇函数在关于原点对称的单调区间内有相同的单调性，偶函数在关于原点对称的单调区间内有相反的单调性.‎ ‎(3)周期性：①若y＝f(x)对x∈R，f(x＋a)＝f(x－a)或f(x＋2a)＝f(x)(a>0)恒成立，则y＝f(x)是周期为2a的周期函数.‎ ‎②若y＝f(x)是偶函数，其图象又关于直线x＝a对称，则f(x)是周期为2|a|的周期函数.‎ ‎③若y＝f(x)是奇函数，其图象又关于直线x＝a对称，则f(x)是周期为4|a|的周期函数.‎ ‎④若f(x＋a)＝－f(x)，则y＝f(x)是周期为2|a|的周期函数.‎ 易错提醒　错用集合运算符号致误：函数的多个单调区间若不连续，不能用符号“∪”连接，可用“和”或“，”连接.‎ 热点一　函数及其表示 ‎【例1】 (1)函数y＝的定义域为(　　)‎ A.(－∞，1]‎ B.[－1，1]‎ C.∪ D.∪ ‎(2)(2018·全国Ⅰ卷)设函数f(x)＝则满足f(x＋1)0，由f(a)＝－2，知－log2(a＋1)＋2＝－2，∴a＝15.故f(14－a)＝f(－1)＝2－1＋1＝1.‎ 答案　(1)D　(2)1‎ 热点二　函数的图象及应用 ‎【例2】 (1)(2018·浙江卷)函数y＝2|x|sin 2x的图象可能是(　　)‎ ‎(2)(2018·合肥调研)已知函数f(x)＝ 若f(x1)＝f(x2)＝f(x3)(x1，x2，x3互不相等)，且x1＋x2＋x3的取值范围为(1，8)，则实数m的值为________.‎ 解析　(1)设f(x)＝2|x|sin 2x，其定义域关于坐标原点对称，又f(－x)＝2|－x|·sin(－2x)＝－f(x)，所以y＝f(x)是奇函数，故排除选项A，B；令f(x)＝0，则sin 2x＝0，所以x＝(k∈Z)，故排除选项C.故选D.‎ ‎(2)作出f(x)的图象，如图所示，可令x12，排除A，C.又当x→＋∞时，y→＋∞，B项不满足，D满足.‎ ‎(2)画出y＝|f(x)|＝|2x－1|与y＝g(x)＝1－x2的图象，它们交于A，B两点.由“规定”，在A，B两侧，|f(x)|≥g(x)，故h(x)＝|f(x)|；在A，B之间，|f(x)|log25.1>2>20.8，且a＝g(－log25.1)＝g(log25.1)，‎ ‎∴g(3)>g(log25.1)>g(20.8)，则c>a>b.‎ 法二　(特殊化)取f(x)＝x，则g(x)＝x2为偶函数且在(0，＋∞)上单调递增，又3>log25.1>20.8，‎ 从而可得c>a>b.‎ 答案　(1)D　(2)C 探究提高　1.利用函数的奇偶性和周期性可以转化函数的解析式、图象和性质，把不在已知区间上的问题，转化到已知区间上求解.‎ ‎2.函数单调性应用：可以比较大小、求函数最值、解不等式、证明方程根的唯一性.‎ ‎【训练3】 (1)(2018·潍坊模拟)若函数f(x)＝ 为奇函数，则 f(g(－3))＝(　　)‎ A.－3 B.－2 C.－1 D.0‎ ‎(2)已知偶函数f(x)在[0，＋∞)上单调递减，且f(2)＝0.若f(x－1)>0，则x的取值范围是________.‎ 解析　(1)由题意得g(－3)＝f(－3)＝－f(3)＝2－log33＝1.因此f[g(－3)]＝f(1)＝log31－2＝－2.‎ ‎(2)由题意知f(x－1)>f(2).‎ 又因为f(x)是偶函数且在[0，＋∞)上单调递减，‎ 所以f(|x－1|)>f(2)，即|x－1|<2，解得－10，忽视ln x≠0的限制.‎ ‎2.如果一个奇函数f(x)在原点处有意义，即f(0)有意义，那么一定有f(0)＝0；若f(x)为偶函数，则f(|x|)＝f(x).‎ ‎3.三种作函数图象的基本思想方法 ‎(1)通过函数图象变换利用已知函数图象作图；‎ ‎(2)对函数解析式进行恒等变换，转化为已知方程对应的曲线；‎ ‎(3)通过研究函数的性质，明确函数图象的位置和形状.‎ ‎4.函数是中学数学的核心，函数思想是重要的思想方法，利用函数思想研究方程(不等式)才能抓住问题的本质，对于给定的函数若不能直接求解或画出图形，常会通过分解转化为两个函数图象，数形结合直观求解.‎ 一、选择题 ‎1.设f(x)＝若f(a)＝f(a＋1)，则f＝(　　)‎ A.2 B.4 C.6 D.8‎ 解析　由已知得a>0，∴a＋1>1，‎ ‎∵f(a)＝f(a＋1)，∴＝2(a＋1－1)，‎ 解得a＝，∴f ＝f(4)＝2(4－1)＝6.‎ 答案　C ‎2.(2018·西安质检)函数f(x)＝的图象是(　　)‎ 解析　f(x)＝为奇函数，排除选项A，B，由f(x)＝0，知x＝0或x＝±1，选项D满足.‎ 答案　D ‎3.(2018·全国Ⅲ卷)下列函数中，其图象与函数y＝ln x的图象关于直线x＝1对称的是(　　)‎ A.y＝ln(1－x) B.y＝ln(2－x)‎ C.y＝ln(1＋x) D.y＝ln(2＋x)‎ 解析　法一　设所求函数图象上任一点的坐标为(x，y)，则其关于直线x＝1的对称点的坐标为(2－x，y)，由对称性知点(2－x，y)在函数f(x)＝ln x的图象上，所以y＝ln(2－x).‎ 法二　由题意知，对称轴上的点(1，0)既在函数y＝ln x的图象上也在所求函数的图象上，代入选项中的函数表达式逐一检验，排除A，C，D，选B.‎ 答案　B ‎4.已知定义在R上的函数f(x)＝2|x－m|－1(m为实数)为偶函数，记a＝f(log0.53)，b＝f(log25)，c＝f(2m)，则a，b，c的大小关系为(　　)‎ A.a＜b＜c B.a＜c＜b C.c＜a＜b D.c＜b＜a 解析　由f(x)＝2|x－m|－1是偶函数可知m＝0，‎ 所以f(x)＝2|x|－1.‎ 所以a＝f(log0.53)＝2|log0.53|－1＝2log23－1＝2，‎ b＝f(log25)＝2|log25|－1＝2log25－1＝4，‎ c＝f(0)＝2|0|－1＝0，所以c－1.‎ 答案　{x|x>－1}‎ ‎8.已知函数f(x)是奇函数，当x>0时，f(x)＝ax(a>0且a≠1)，且f(log4)＝－3，则a的值为________.‎ 解析　∵奇函数f(x)满足f(log4)＝－3，而log4＝－2<0，∴f(－2)＝－3，即f(2)＝3，‎ 又∵当x>0时，f(x)＝ax(a>0且a≠1)，又2>0，‎ ‎∴f(2)＝a2＝3，解之得a＝.‎ 答案　 ‎9.如图，函数f(x)的图象为折线ACB，则不等式f(x)≥log2(x＋1)的解集是________.‎ 解析　在同一坐标系中画出函数f(x)与y＝log2(x＋1)的图象，如图所示.‎ 根据图象，当x∈(－1，1]时，y＝f(x)的图象在y＝log2(x＋1)图象的上方.‎ 所以不等式的解集为(－1，1].‎ 答案　(－1，1]‎ 三、解答题 ‎10.(2018·深圳中学调研)已知函数f(x)＝a－.‎ ‎(1)求f(0)；‎ ‎(2)探究f(x)的单调性，并证明你的结论；‎ ‎(3)若f(x)为奇函数，求满足f(ax)0，2x2＋1>0.‎ ‎∴f(x1)－f(x2)<0，即f(x1)

查看更多