- 2021-06-30 发布 |
- 37.5 KB |
- 22页

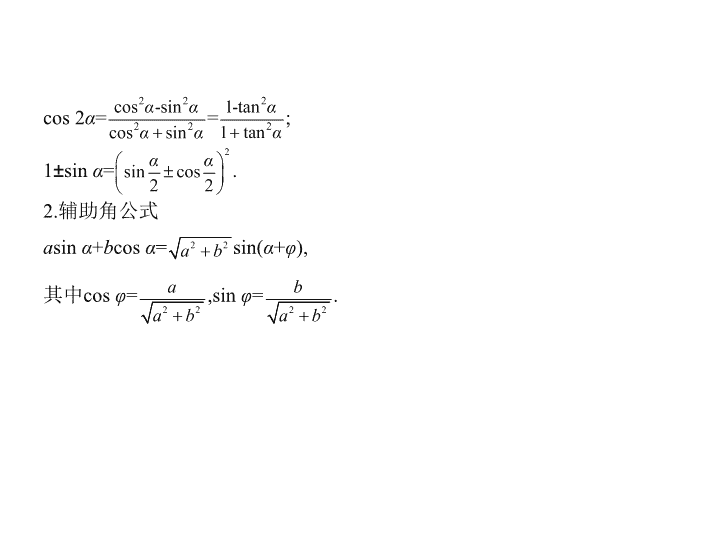
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届课标版高考文科数学大一轮复习课件:§4-2 三角恒等变换(讲解部分)
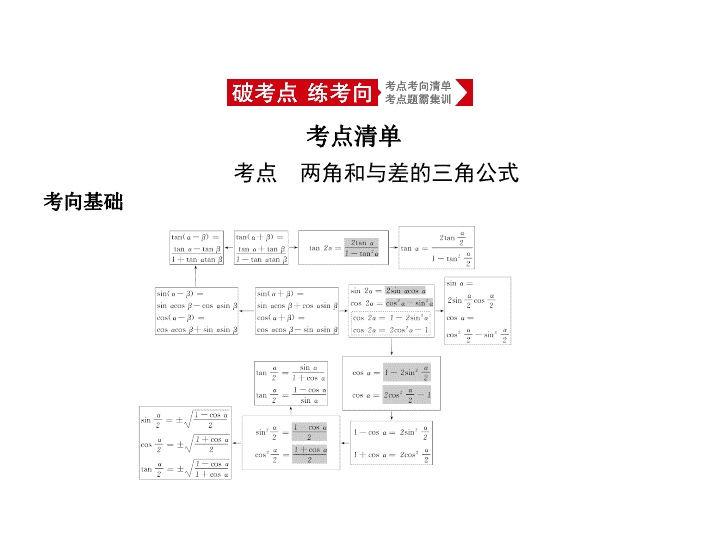
考点 两角和与差的三角公式 考点清单 考向基础 【知识拓展】 1.公式的变形与应用 (1)两角和与差的正切公式的变形 tan α +tan β =tan( α + β )(1-tan α tan β ); tan α -tan β =tan( α - β )(1+tan α tan β ). (2)升幂公式 1+cos α =2cos 2 ;1-cos α =2sin 2 . (3)降幂公式 sin 2 α = ;cos 2 α = . (4)其他常用变形 sin 2 α = = ; cos 2 α = = ; 1 ± sin α = . 2.辅助角公式 a sin α + b cos α = sin( α + φ ), 其中cos φ = ,sin φ = . 考向突破 考向一 三角函数式的化简 例1 化简: · · = . 解析 · · = · · = · = · = =tan . 答案 tan 考向二 三角函数式的求值 例2 (2018湖南永州祁阳二模)已知tan α + = ,则cos 2 - α = ( ) A. B. C. D. 解析 ∵tan = , ∴cos 2 =sin 2 = = = = .故选B. 答案 B 例3 (2020届湖南邵阳9月联考,14)计算:sin 10 ° ·sin 30 ° ·sin 50 ° ·sin 70 ° = . 解析 解法一:sin 10 ° ·sin 30 ° ·sin 50 ° ·sin 70 ° = cos 20 ° ·cos 40 ° ·cos 80 ° = = = = = . 解法二:令 m =sin 10 ° sin 50 ° sin 70 ° , n =cos 10 ° cos 50 ° ·cos 70 ° , 则 mn =sin 10 ° cos 10 ° sin 50 ° cos 50 ° sin 70 ° cos 70 ° = sin 20 ° · sin 100 ° · sin 140 ° = sin 20 ° ·sin 80 ° ·sin 40 ° = cos 70 ° ·cos 10 ° ·cos 50 ° = n , 而 n ≠ 0, ∴ m = ,从而有sin 10 ° ·sin 30 ° ·sin 50 ° ·sin 70 ° = . 答案 考向三 辅助角公式的应用 例4 已知 x ∈ ,则函数 f ( x )=5 cos 2 x + sin 2 x -4sin x cos x 的最小值为 . 解析 f ( x )=5 cos 2 x + sin 2 x -4sin x cos x = +4 cos 2 x -2sin 2 x = +2 (cos 2 x +1)-2sin 2 x =3 -2sin 2 x +2 cos 2 x =3 -4sin . ∵ x ∈ ,∴2 x - ∈ , ∴sin ∈ . ∴当2 x - = ,即 x = 时, f ( x )取得最小值,其最小值为3 -2 . 答案 3 -2 方法1 三角函数式的化简方法 1.化简原则 (1) 一看“角” ,这是最重要的一环,通过看角之间的差别与联系,把角合理 地拆分,从而正确运用公式; (2) 二看“函数名称” ,看函数名称之间的差异,从而确定要使用的公式; (3) 三看“结构特征” ,分析结构特征可以帮助我们找到变形的方向,常见 的有“遇到分式要通分”“遇到根式一般要升幂”等. 方法技巧 2.化简要求 (1)使三角函数式的项数最少、次数最低、角与函数名称的种类最少; (2)尽量使分母不含三角函数; (3)尽量使被开方数不含三角函数等. 3.化简方法 (1)直接应用公式进行降次、消项; (2)切化弦、异角化同角、异次化同次、异名化同名; (3)三角公式的逆用等. 例1 化简:sin 2 α ·sin 2 β +cos 2 α ·cos 2 β - cos 2 α ·cos 2 β = . 解析 解法一(从“角”入手,“倍角”变“单角”): 原式=sin 2 α ·sin 2 β +cos 2 α ·cos 2 β - (2cos 2 α -1)(2cos 2 β -1) =sin 2 α ·sin 2 β +cos 2 α ·cos 2 β - (4cos 2 α ·cos 2 β -2cos 2 α -2cos 2 β +1) =sin 2 α ·sin 2 β -cos 2 α ·cos 2 β +cos 2 α +cos 2 β - =sin 2 α ·sin 2 β +cos 2 α ·sin 2 β +cos 2 β - =sin 2 β +cos 2 β - =1- = . 解法二(从“名”入手,异名化同名): 原式=sin 2 α ·sin 2 β +(1-sin 2 α )·cos 2 β - cos 2 α ·cos 2 β =cos 2 β -sin 2 α (cos 2 β -sin 2 β )- cos 2 α ·cos 2 β =cos 2 β -sin 2 α ·cos 2 β - cos 2 α ·cos 2 β =cos 2 β -cos 2 β · = -cos 2 β = - cos 2 β = . 解法三(从“幂”入手,利用降幂公式先降次): 原式= · + · - cos 2 α ·cos 2 β = (1+cos 2 α cos 2 β -cos 2 α -cos 2 β )+ (1+cos 2 α cos 2 β +cos 2 α +cos 2 β )- cos 2 α cos 2 β = + = . 答案 例2 已知 α 为第二象限角,则cos α +sin α · = . 解析 因为 α 为第二象限角,所以sin α >0,cos α <0. 因为 = = = = , = = = = , 所以cos α +sin α =cos α · +sin α · =sin α -cos α . 答案 sin α -cos α 方法2 三角函数式的求值方法 1.“给角求值”:一般给出的角都是非特殊角,从表面上看是很难的,但仔细 观察,非特殊角与特殊角总有一定的关系,解题时,要利用观察得到的关系, 结合公式转化为特殊角求解. 2.“给值求值”:给出某些角的三角函数式的值,求另外一些与该角有关联 的角的三角函数式的值,解题关键在于“变角”,使它们的角相同或具有某 种关系. 3.“给值求角”:实质是转化为“给值求值”,先求角的某一三角函数值,再 求角的范围,最后确定角的大小. 例3 (1)(2018湖北八校第一次联考,10)已知3π< θ <4π,且 + = ,则 θ = ( ) A. 或 B. 或 C. 或 D. 或 (2)(2020届广东佛山一中9月月考,8)已知 α , β 为锐角,且tan α = ,cos( α + β )= ,则cos 2 β = ( ) A. B. C. D. 解析 (1)∵3π< θ <4π,∴ < <2π,∴cos >0,sin <0,∴ + = + =cos -sin = cos = ,∴cos = ,∴ + = +2 k π( k ∈Z)或 + =- +2 k π( k ∈Z),即 θ =- +4 k π( k ∈Z)或 θ =- +4 k π( k ∈Z),又∵3π< θ <4π,∴ θ = 或 .故选D. (2)∵ α , β ∈ ,∴ α + β ∈(0,π). ∵cos( α + β )= ,∴sin( α + β )= . ∵tan α = ,∴sin α = ,cos α = . ∴cos β =cos[( α + β )- α ]=cos( α + β )cos α +sin( α + β )sin α = × + × = , ∴cos 2 β =2cos 2 β -1=2 × -1= ,故选C. 答案 (1)D (2)C查看更多