2019届二轮复习（理）专题五立体几何5-3立体几何中的向量方法课件（41张）（全国通用）

2019届二轮复习（理）专题五立体几何5-3立体几何中的向量方法课件（41张）（全国通用）

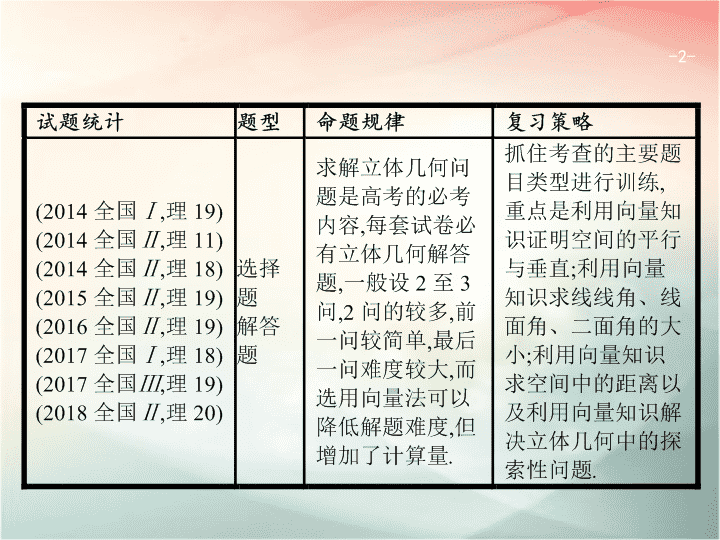
5.3 　立体几何中的向量方法 - 2 - - 3 - 命题热点一 命题热点二 命题热点三 用空间向量证明空间的平行与垂直 【思考】 如何用空间向量证明空间的平行与垂直? 例 1 已知直三棱柱 ABC-A 1 B 1 C 1 中, AC ⊥ BC , D 为 AB 的中点, AC=BC=BB 1 . ( 1)求证: BC 1 ⊥ AB 1 ; (2)求证: BC 1 ∥ 平面 CA 1 D. - 4 - 命题热点一 命题热点二 命题热点三 证明： 如图 , 以 C 1 为原点 , C 1 A 1 , C 1 B 1 , C 1 C 所在直线分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系 . 由 AC=BC=BB 1 , 设 AC= 2, 则 A (2,0,2), B (0,2,2), C (0,0,2), A 1 (2,0,0), B 1 (0,2,0), C 1 (0,0,0), D (1,1,2) . - 5 - 命题热点一 命题热点二 命题热点三 - 6 - 命题热点一 命题热点二 命题热点三 题后反思 用向量方法证明空间线面位置关系的方法 : 设直线 l 1 , l 2 的方向向量分别为 a , b , 平面 α , β 的法向量分别为 e 1 , e 2 , A , B , C 分别为平面 α 内的相异且不共线的三点 ( 其中 l 1 与 l 2 不重合 , α 与 β 不重合 ), 则 (1) l 1 ∥ l 2 ⇔ a ∥ b ⇔ 存在实数 λ , 使 b = λ a ( a ≠ 0 ); l 1 ⊥ l 2 ⇔ a ⊥ b ⇔ a · b = 0 . (2) l 1 ⊥ α ⇔ a ∥ e 1 ⇔ 存在实数 λ , 使 e 1 = λ a ( a ≠ 0 ); l 1 ∥ α ⇔ a · e 1 = 0 ⇔ 存在非零实数 λ 1 , λ 2 , 使 a = λ 1 ( 3) α ∥ β ⇔ e 1 ∥ e 2 ⇔ 存在实数 λ , 使 e 2 = λ e 1 ( e 1 ≠ 0 ); α ⊥ β ⇔ e 1 ⊥ e 2 ⇔ e 1 · e 2 = 0 . - 7 - 命题热点一 命题热点二 命题热点三 对点训练 1 在直三棱柱 ABC-A 1 B 1 C 1 中 , ∠ ABC= 90 ° , BC= 2, CC 1 = 4, 点 E 在线段 BB 1 上 , 且 EB 1 = 1, D , F , G 分别为 CC 1 , C 1 B 1 , C 1 A 1 的中点 . 求证 :(1) B 1 D ⊥ 平面 ABD ; (2) 平面 EGF ∥ 平面 ABD. 证明： (1) 以 B 为坐标原点 , BA , BC , BB 1 所在直线分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系 , 如图 . 则 B (0,0,0), D (0,2,2), B 1 (0,0,4), 设 BA=a , 则 A ( a ,0,0), - 8 - 命题热点一 命题热点二 命题热点三 即 B 1 D ⊥ EG , B 1 D ⊥ EF , 又 EG ∩ EF=E , 因此 B 1 D ⊥ 平面 EGF. 结合 (1) 可知平面 EGF ∥ 平面 ABD. - 9 - 命题热点一 命题热点二 命题热点三 利用向量求空间角 【思考】 如何用空间向量求空间角? 例 2 如 图,四棱锥 P-ABCD 中,侧面 PAD 为等边三角形且垂直于底面 ABCD , AB=BC= AD , ∠ BAD= ∠ ABC= 90°, E 是 PD 的中点 . (1)证明:直线 CE ∥ 平面 PAB ; (2)点 M 在棱 PC 上,且直线 BM 与底面 ABCD 所成角为45°,求二面角 M-AB-D 的余弦值 . - 10 - 命题热点一 命题热点二 命题热点三 - 11 - 命题热点一 命题热点二 命题热点三 - 12 - 命题热点一 命题热点二 命题热点三 - 13 - 命题热点一 命题热点二 命题热点三 - 14 - 命题热点一 命题热点二 命题热点三 题后反思 用向量求空间角的方法 : 设直线 l 1 , l 2 的方向向量分别为 a , b , 平面 α , β 的法向量分别为 n , m . - 15 - 命题热点一 命题热点二 命题热点三 对点训练 2 如图 , 四面体 ABCD 中 , △ ABC 是正三角形 , △ ACD 是直角三角形 , ∠ ABD= ∠ CBD , AB=BD. (1) 证明 : 平面 ACD ⊥ 平面 ABC ; (2) 过 AC 的平面交 BD 于点 E , 若平面 AEC 把四面体 ABCD 分成体积相等的两部分 , 求二面角 D-AE-C 的余弦值 . - 16 - 命题热点一 命题热点二 命题热点三 (1) 证明 : 由题设可得 , △ ABD ≌ △ CBD , 从而 AD=DC. 又 △ ACD 是直角三角形 , 所以 ∠ ADC= 90 ° . 取 AC 的中点 O , 连接 DO , BO , 则 DO ⊥ AC , DO=AO. 又由于 △ ABC 是正三角形 , 故 BO ⊥ AC. 所以 ∠ DOB 为二面角 D-AC-B 的平面角 . 在 Rt △ AOB 中 , BO 2 +AO 2 =AB 2 , 又 AB=BD , 所以 BO 2 +DO 2 =BO 2 +AO 2 =AB 2 =BD 2 , 故 ∠ DOB= 90 ° . 所以平面 ACD ⊥ 平面 ABC. - 17 - 命题热点一 命题热点二 命题热点三 - 18 - 命题热点一 命题热点二 命题热点三 - 19 - 命题热点一 命题热点二 命题热点三 对点训练 3 (2018 浙江 ,19) 如图 , 已知多面体 ABCA 1 B 1 C 1 , A 1 A , B 1 B , C 1 C 均垂直于平面 ABC , ∠ ABC= 120 ° , A 1 A= 4, C 1 C= 1, AB=BC=B 1 B= 2 . (1) 证明 : AB 1 ⊥ 平面 A 1 B 1 C 1 ; (2) 求直线 AC 1 与平面 ABB 1 所成的角的正弦值 . - 20 - 命题热点一 命题热点二 命题热点三 - 21 - 命题热点一 命题热点二 命题热点三 - 22 - 命题热点一 命题热点二 命题热点三 解法二 (1) 证明 : 如图 , 以 AC 的中点 O 为原点 , 分别以射线 OB , OC 为 x , y 轴的正半轴 , 建立空间直角坐标系 O-xyz. - 23 - 命题热点一 命题热点二 命题热点三 - 24 - 命题热点一 命题热点二 命题热点三 用空间向量求空间中的距离 【思考】 如何用空间向量求空间中的距离? 例 3 如图,在四棱锥 P-ABCD 中,底面四边形 ABCD 是正方形,侧面 PDC 是边长为 a 的正三角形,且侧面 PDC ⊥ 底面 ABCD , E 为 PC 的中点 . (1)求异面直线 PA 与 DE 所成角的余弦值; (2)求点 D 到平面 PAB 的距离 . - 25 - 命题热点一 命题热点二 命题热点三 解： 如图 , 取 DC 的中点 O , 连接 PO , ∵ △ PDC 为正三角形 , ∴ PO ⊥ DC. 又侧面 PDC ⊥ 底面 ABCD , ∴ PO ⊥ 底面 ABCD. 如图建立空间直角坐标系 O-xyz. - 26 - 命题热点一 命题热点二 命题热点三 - 27 - 命题热点一 命题热点二 命题热点三 题后反思 求空间中距离的方法 : (1) 直线到平面的距离 , 两平行平面间的距离均可转化为点到平面的距离 . (2) 点 P 到平面 α 的距离 d = ( 其中 n 为 α 的法向量 , M 为 α 内任一点 ) . (3) 设直线 n 的方向向量为 n , 直线 n 与异面直线 a , b 都垂直 , A 是直线 a 上任一点 , B 是直线 b 上任一点 , 则异面直线 a , b 的距离 d = - 28 - 命题热点一 命题热点二 命题热点三 对点训练 4 如图 , 在四棱锥 P-ABCD 中 , PA ⊥ 底面 ABCD , AB ⊥ AD , AB+AD= 4, CD= , ∠ CDA= 45 ° . (1) 求证 : 平面 PAB ⊥ 平面 PAD. (2) 设 AB=AP. ① 若直线 PB 与平面 PCD 所成的角为 30 ° , 求线段 AB 的长 ; ② 在线段 AD 上是否存在一个点 G , 使得点 G 到点 P , B , C , D 的距离都相等 ? 说明理由 . - 29 - 命题热点一 命题热点二 命题热点三 (1) 证明： 因为 PA ⊥ 平面 ABCD , AB ⊂ 平面 ABCD , 所以 PA ⊥ AB. 因为 AB ⊥ AD , PA ∩ AD=A , 所以 AB ⊥ 平面 PAD. 又 AB ⊂ 平面 PAB , 所以平面 PAB ⊥ 平面 PAD. (2) 解： 以 A 为坐标原点 , 建立空间直角坐标系 A-xyz , 如图 . 在平面 ABCD 内作 CE ∥ AB 交 AD 于点 E , 则 CE ⊥ AD. 在 Rt △ CDE 中 , DE=CD· cos 45 ° = 1, CE=CD· sin 45 ° = 1 . 设 AB=AP=t , 则 B ( t ,0,0), P (0,0, t ) . 由 AB+AD= 4, 得 AD= 4 -t , 所以 E (0,3 -t ,0), C (1,3 -t ,0), D (0,4 -t ,0), - 30 - 命题热点一 命题热点二 命题热点三 - 31 - 命题热点一 命题热点二 命题热点三 ② 假设在线段 AD 上存在一个点 G , 使得点 G 到点 P , B , C , D 的距离都相等 . 由 ①② 消去 t , 化简得 m 2 - 3 m+ 4 = 0 . ③ 因为方程 ③ 没有实数根 , 所以在线段 AD 上不存在一个点 G , 使得点 G 到点 P , C , D 的距离都相等 . 从而 , 在线段 AD 上不存在一个点 G , 使得点 G 到点 P , B , C , D 的距离都相等 . - 32 - 规律总结 拓展演练 1 . 用空间向量解决立体几何问题时,要根据情况选择,常建立空间直角坐标系,利用空间向量知识解决立体几何问题 . 用空间向量解决的主要立体几何问题有平行、垂直、求角、求距离等 . 2 . 用向量证明空间中的平行关系: (1)设直线 l 1 和 l 2 的方向向量分别为 v 1 和 v 2 ,则 l 1 ∥ l 2 (或 l 1 与 l 2 重合) ⇔ v 1 ∥ v 2 . (2)设直线 l 的方向向量为 v ,与平面 α 共面的两个不共线向量 v 1 和 v 2 ,则 l ∥ α 或 l ⊂ α ⇔ 存在两个实数 x , y ,使 v =x v 1 +y v 2 . (3)设直线 l 的方向向量为 v ,平面 α 的法向量为 u ,则 l ∥ α 或 l ⊂ α ⇔ v ⊥ u . (4)设平面 α 和 β 的法向量分别为 u 1 , u 2 ,则 α ∥ β ⇔ u 1 ∥ u 2 . - 33 - 规律总结 拓展演练 3 . 用向量证明空间中的垂直关系: (1)设直线 l 1 和 l 2 的方向向量分别为 v 1 和 v 2 ,则 l 1 ⊥ l 2 ⇔ v 1 ⊥ v 2 ⇔ v 1 · v 2 = 0 . (2)设直线 l 的方向向量为 v ,平面 α 的法向量为 u ,则 l ⊥ α ⇔ v ∥ u . (3)设平面 α 和 β 的法向量分别为 u 1 和 u 2 ,则 α ⊥ β ⇔ u 1 ⊥ u 2 ⇔ u 1 · u 2 = 0 . 4 . 两异面直线所成的角不一定是它们的方向向量的夹角;两平面的法向量的夹角与两平面的二面角相等或互补;直线的方向向量与平面的法向量的夹角与线面角的余角相等或互补 . (1)两条异面直线所成的角:设异面直线 a , b 所成的角为 θ , a , b 的方向向量为 a , b ,其夹角为 φ ,则有cos θ =| cos φ |= . - 34 - 规律总结 拓展演练 (2) 直线和平面所成的角 : 如图 ,sin φ=| cos θ|= . (3) 平面 α 与平面 β 所成的二面角为 θ , 两平面的法向量分别为 m , n , 则 | cos θ|= . - 35 - 规律总结 拓展演练 5 . 点到平面的距离的向量求法 : 如图,设 AB 为平面 α 的一条斜线段, n 为平面 α 的法向量,则点 B 到平面 α 的距离 d = . - 36 - 规律总结 拓展演练 1 . 在直三棱柱 ABC-A 1 B 1 C 1 中 , ∠ BCA= 90 ° , M , N 分别是 A 1 B 1 , A 1 C 1 的中点 , BC=CA=CC 1 , 则 BM 与 AN 所成角的余弦值为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 37 - 规律总结 拓展演练 2 . 已知两平面的法向量分别为 m = (0,1,0), n = (0,1,1),则两平面所成二面角的大小为 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 38 - 规律总结 拓展演练 3 . (2018 天津 , 理 17) 如图 , AD ∥ BC 且 AD= 2 BC , AD ⊥ CD , EG ∥ AD 且 EG=AD , CD ∥ FG 且 CD= 2 FG , DG ⊥ 平面 ABCD , DA=DC=DG= 2 . (1) 若 M 为 CF 的中点 , N 为 EG 的中点 , 求证 : MN ∥ 平面 CDE ; (2) 求二面角 E-BC-F 的正弦值 ; (3) 若点 P 在线段 DG 上 , 且直线 BP 与平面 ADGE 所成的角为 60 ° , 求线段 DP 的长 . - 39 - 规律总结 拓展演练 - 40 - 规律总结 拓展演练 - 41 - 规律总结 拓展演练