2019届二轮复习4-5对数函数课件(13张)(全国通用)
4.5
对数函数
【考纲要求】 理解对数函数的概念、图象及性质
.
【学习重点】 对数函数的概念、图象及性质
.
一、自主学习
(
一
)
知识归纳
1
.
对数函数的定义
一般地
,
我们把形如
y=
log
a
x
(
a>
0,
a
≠1)
的函数叫做对数函数
.
2
.
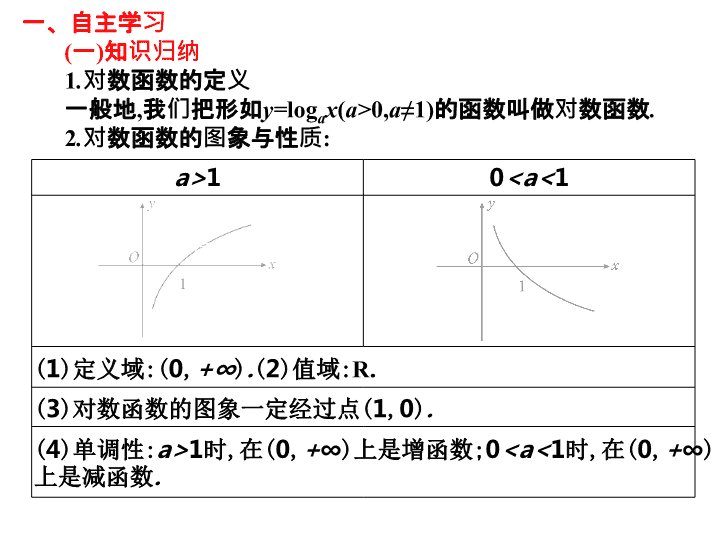
对数函数的图象与性质
:
a>
1
0
1
时
,
在
(
0
,
+
∞
)
上是增函数
;
0
log
3
0.7 B.lg3>lg
π
C.log
0.5
6>log
0.5
7 D.ln4>ln4.1
2
.
如果
log
3
(log
2
x
)
=
1,
则
x=
(
)
A.3 B.2 C.8 D.0
3
.
若
log
(
x+
1)
(
x+
1)
=
1,
则
x
的取值范围是
(
)
A.(
-
1,
+∞
) B.(
-
1,0)∪(0,
+∞
)
C.R D.(
-∞
,
-
1)∪(
-
1,
+∞
)
【
答案
】B
(2,0)
(
-
1,1)
4
.
已知
log
4
(2
x
)
>
0,
则
x
∈
.
5
.
对数函数
y=
log
a
(
x-
1),(
a>
0,
a
≠1)
恒过定点
.
6
.
函数
f
(
x
)
=
lg(1
-x
2
)
的定义域是
.
二、探究提高
【例
5
】 已知函数
f
(
x
)
=
log
5
(
x
2
-
4),
求
:
(1)
函数
f
(
x
)
的定义域
;
(2)
判断函数
f
(
x
)
的奇偶性
;
(3)
求该函数的单调增区间
.
【解】
(1)
依题意
x
2
-
4
>
0,
∴x<-
2
或
x>
2,
∴
函数的定义域为
A=
(
-∞
,
-
2)∪(2,
+∞
)
.
(2)
当
x
∈
A
时
,
-x
∈
A.
因为
f
(
-x
)
=
log
5
[(
-x
)
2
-
4]
=
log
5
(
x
2
-
4)
=f
(
x
),
所以函数
f
(
x
)
是偶函数
.
(3)
设
t=x
2
-
4,
f
(
x
)
=
log
5
t
是增函数
,
而
t=x
2
-
4
的单调增区间为
(0,
+∞
),
所以函数
f
(
x
)
的增区间是
(0,
+∞
)∩((
-∞
,
-
2)∪(2,
+∞
))
=
(2,
+∞
)
.
三、达标训练
【
答案
】C
【
答案
】A
【
答案
】C
>
<
lg5
(2,2)
(1,2)
9
.
求不等式
log
0
.
3
(3
x-
4)
<
log
0
.
3
(2
x+
5)
的解集
.
10
.
已知函数
f
(
x
)
=
1
+
log
a
(
x
2
-
2
x
),
其中
a>
0,
a
≠1
且
f
(3)
=
2
.
(1)
求
f
(
x
)
的定义域
;
(2)
求不等式
f
(
x
)≥2
的解集
.
解
:(1)
由题得
x
2
-
2
x>
0
解得
x<
0
或
x>
2
.
所以原函数的定义域为
{
x|x<
0
或
x>
2}
.
(2)
由
f
(
x
)
=
1
+
log
a
(
x
2
-
2
x
),
则
f
(3)
=
1
+
log
a
(3
2
-
6)
=
2
.
解得
a=
3
.
由
f
(
x
)
=
1
+
log
3
(
x
2
-
2
x
)≥2,
则
x
2
-
2
x
≥3
.
解不等式得
x
≥3
或
x
≤
-
1
.
所以不等式
f
(
x
)≥2
的解集是
{
x|x
≥3
或
x
≤
-
1}
.