- 2021-06-30 发布 |
- 37.5 KB |
- 9页

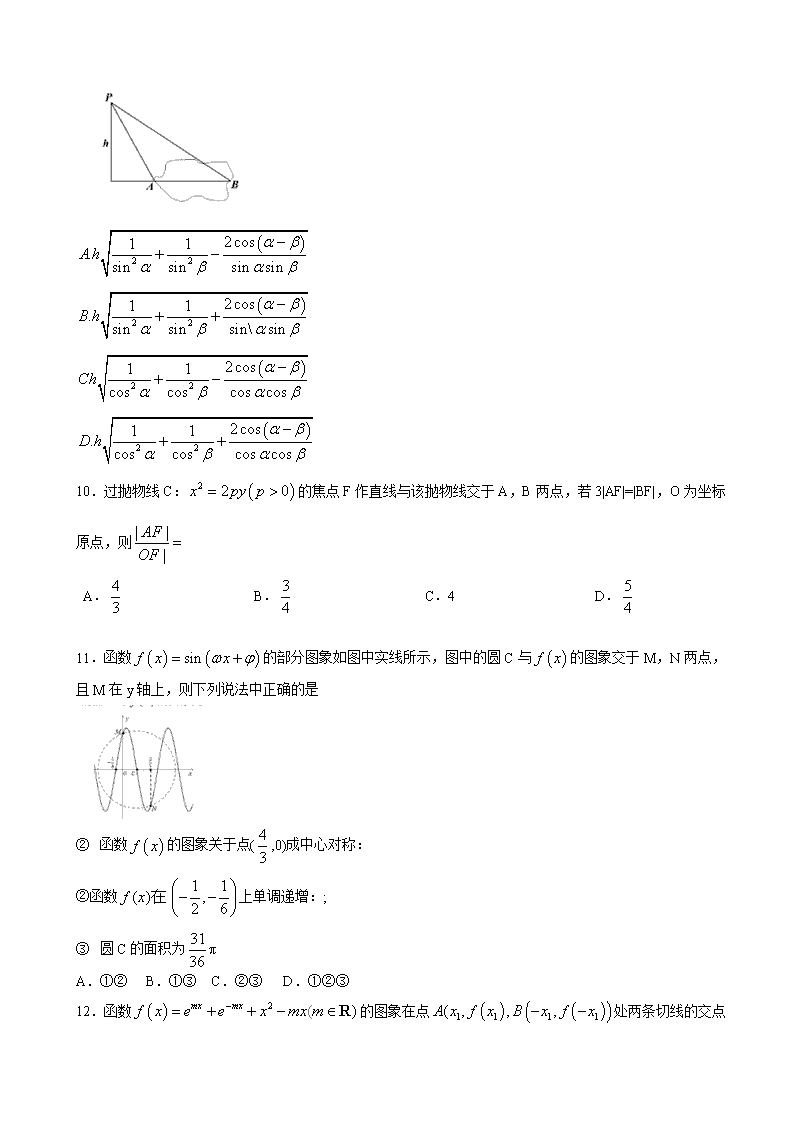

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
吉林省长春市2020届高三质量监测(四)(四模)数学(理)试题
长春市2020届高三质量监测(四) 理科数学 一、选择题:本题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的。 1.设集合则 D. 2.在等比数列中则a9= A B. C.9 D.12 3.设复数下列说法正确的是 A.的虚部是yi; B. C.若x=0,则复数为纯虚数; D.若满足,则z在复平面内对应点的轨迹是圆. 4.树立劳动观念对人的健康成长至关重要,某实践小组共有4名男生,2名女生,现从中选出4人参加校园植树活动,其中至少有一名女生的选法共有 A.8种 B.9种 C.12种 D.14种 5. A. B. C. D. 6.田径比赛跳高项目中,在横杆高度设定后,运动员有三次试跳机会,只要有一次试跳成功即完成本轮比赛。在某学校运动会跳高决赛中,某跳高运动员成功越过现有高度即可成为本次比赛的冠军,结合平时训练数据,每次试跳他能成功越过这个高度的概率为0.8(每次试跳之间互不影响),则本次比赛他获得冠军的概率是 A.0.832 B.0.920 C.0.960 D.0.992 7.已知则a,b,c的大小关系是 A. B . C. D. 8.已知直线a和平面α、β有如下关系:②α∥β,③α⊥β,④α∥a,则下列命题为真的是 A.①③½④ B.①④½③ C.③④½① D.②③½④ 9.如图,为测量某公园内湖岸边A,B两处的距离,一无人机在空中P点处测得A,B的俯角分别为α,β,此时无人机的高度为h,则AB的距离为 10.过抛物线C:的焦点F作直线与该抛物线交于A,B两点,若3|AF|=|BF|,O为坐标原点,则 A. B. C.4 D. 11.函数的部分图象如图中实线所示,图中的圆C与的图象交于M,N两点,且M在y轴上,则下列说法中正确的是 ② 函数的图象关于点(,0)成中心对称: ②函数上单调递增:; ③ 圆C的面积为π A.①② B.①③ C.②③ D.①②③ 12.函数的图象在点处两条切线的交点 一定满足 二、填空题:本题共4小题,每小题5分,共20分 13.已知双曲线的离心率为,则双曲线的渐近线方程为 14.执行如图所示的程序框图,若输入则输出s的取值范围是 15.已知向量则△ABC面积为 16.已知正方体的棱长为2,点M,N分别是棱BC,CC1的中点,则二面角的余弦值为,若动点P在正方形BCC1B1(包括边界)内运动,且PA1∥平面则线段的长度范围是.(本小题第一空2分,第二空3分). 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22~23题为选考题,考生根据要求作答. 17.(12分)(一)必考题:共60分 已知数列{an}是等比数列,且公比q不等于1,数列{bn}满足. (Ⅰ)求证:数列{bn}是等差数列; (Ⅱ)若求数列的前n项和Sn. 18.(12分) 如图,四棱锥中,底面ABCD为梯形,AB∥点E为PB的中点,且 CD=2AD=2AB=4,点F在CD上,且. (Ⅰ)求证:EF∥平面PAD; (Ⅱ)若平面PAD⊥平面//PD,求直线PA与平面PBF所成角的正弦值. 19.(12分) 已知椭圆C:与x轴正半轴交于点A,与y轴交于B、C两点. (Ⅰ)求过A,B,C三点的圆E的方程 (Ⅱ)若O为坐标原点,直线l与椭圆C和(Ⅰ)中的圆E分别相切于点P和点Q(P,Q不重合),求直线OP与直线EQ的斜率之积。 20.(12分) 武汉市掀起了轰轰烈烈的“十日大会战”,要在10天之内,对武汉市民做一次全员检测,彻底摸清武汉市的详细情况。 某医院为筛查冠状病毒,需要检验血液是否为阳性,现有份血液样本,有以下两种检验方式: 方案①:将每个人的血分别化验,这时需要验1000次。 方案②:按k个人一组进行随机分组,把从每组k个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这k个人的血就只需检验一次(这时认为每个人的血化验次);否则,若呈阳性。则需对这k个人的血样再分别进行一次化验。这样,该组k个人的血总共需要化验次。假设此次检验中每个人的血样化验呈阳性的概率为p,且这些人之间的试验反应相互独立。 (Ⅰ)设方案②中,某组k个人中每个人的血化验次数为X,求X的分布列; (Ⅱ)设p=0.l.试比较方案②中,k分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以减少多少次?(最后结果四舍五入保留整数) 21.(12分) 已知函数. (Ⅰ)若函数在处有最大值,求a的值; (Ⅱ)当时,判断的零点个数,并说明理由。 (二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做则按所做的第一题计分。 22.[选修4-4坐标系与参数方程](10分) 在平面直角坐标系中,曲线C1的参数方程为 (α为参数),以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系,点A为曲线C1上的动点,点B在线段OA的延长线上,且满足点B的轨迹为C2。 (Ⅰ)求曲线C1,C2的极坐标方程; (Ⅱ)设点M的极坐标为,求△ABM面积的最小值。 23.[选修4-5不等式选讲](10分) 已知函数 (Ⅰ)解不等式: (Ⅱ)设时的最小值为M.若实数a,b,c满足求的最小值.查看更多