备战2014高考数学 高频考点归类分析（真题为例）：函数的单调性、周期性、奇偶性

备战2014高考数学 高频考点归类分析（真题为例）：函数的单调性、周期性、奇偶性

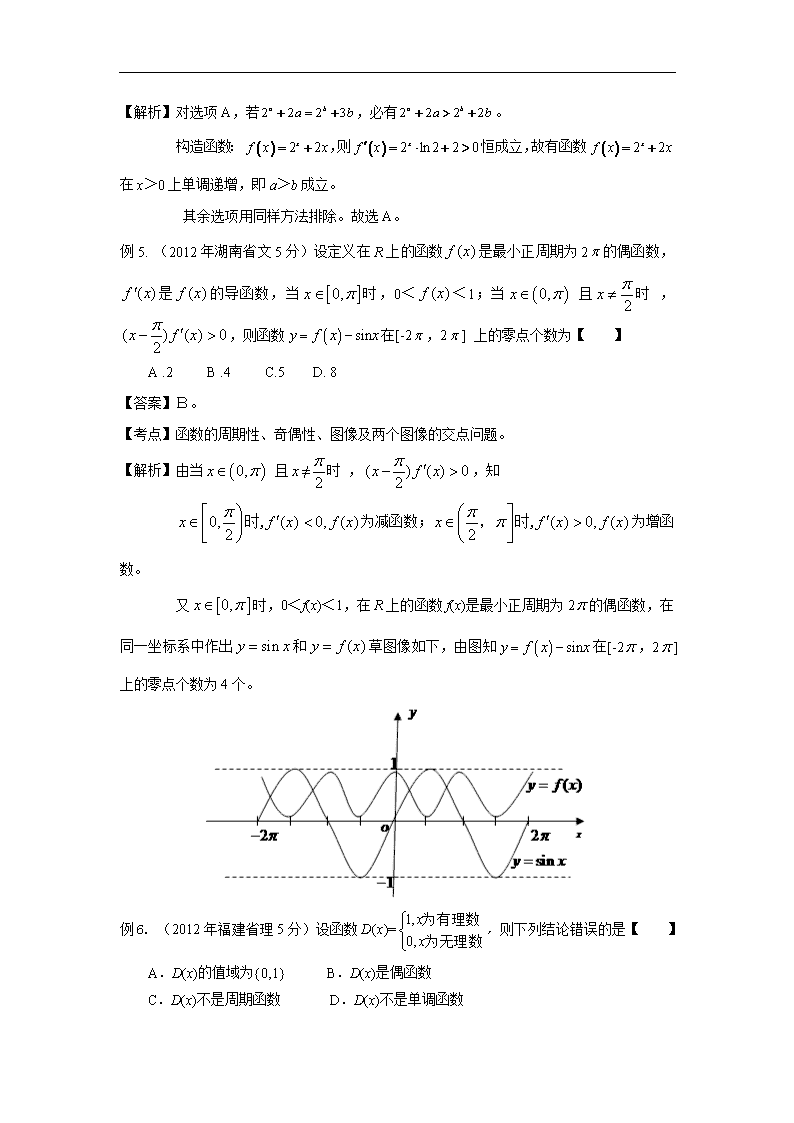
函数的单调性、周期性、奇偶性问题 典型例题： ‎ 例1. （2012年天津市文5分）下列函数中，既是偶函数，又在区间（1,2）内是增函数的为【 】[来源:Z§xx§k.Com]‎ ‎（A） （B），且≠0‎ ‎（C） （D）‎ ‎【答案】B。‎ ‎【考点】函数奇偶性的判断，函数单调性的判断。‎ ‎【分析】利用函数奇偶性的定义可排除C，D，再由“在区间（1，2）内是增函数”可排除A，从而可得答案：‎ 对于A，令，则，∴函数为偶函数。‎ 而在上单调递减，在上单调递增，（1，2）中，‎ 所以在区间（1，2）内不全是增函数，故排除A。‎ 对于B，函数为偶函数，且当时，函数为增函数，所以在上也为增函数，故B满足题意。[来源:Zxxk.Com]‎ 对于C，令 ，则，∴函数为偶函数为奇函数，故可排除C。‎ 对于D，为非奇非偶函数，可排除D。‎ 故选B。 ‎ 例2. （2012年广东省理5分）下列函数中，在区间（0，+∞）上为增函数的是【　　】‎ A． B． C．y= D． ‎ ‎【答案】A。‎ ‎【考点】函数的图象和性质。‎ ‎【解析】利用对数函数的图象和性质可判断A正确；利用幂函数的图象和性质可判断B错误；利用指数函数的图象和性质可判断C正确；利用“对勾”函数的图象和性质可判断D的单调性：‎ A.在（-2，+∞）上为增函数，故在（0，+∞）上为增函数，A正确；‎ B.在[-1，+∞）上为减函数，排除B；‎ C. y=在R上为减函数；排除C；‎ D.在（0，1）上为减函数，在（1，+∞）上为增函数，排除D。‎ 故选 A。‎ 例3. （2012年广东省文5分）下列函数为偶函数的是【 】‎ A． B． C． D．‎ ‎【答案】D。[来源:学科网]‎ ‎【考点】函数偶函数的判断。‎ ‎【解析】函数结合选项，逐项检验是否满足，即可判断：‎ A：，则有，为奇函数；‎ B：，则有，为奇函数；‎ C：，则有，为非奇非偶函数；‎ D：，则有，为偶函数。‎ 故选D。‎ 例4. （2012年浙江省理5分）设，【 】‎ ‎ A．若，则 B．若，则 ‎ C．若，则 D．若，则 ‎【答案】A。‎ ‎【考点】函数的单调性，导数的应用。‎ ‎【解析】对选项A，若，必有。‎ 构造函数：，则恒成立，故有函数在x＞0上单调递增，即a＞b成立。‎ 其余选项用同样方法排除。故选A。‎ 例5. （2012年湖南省文5分）设定义在R上的函数是最小正周期为2的偶函数，是的导函数，当时，0＜＜1；当 且时 ，，则函数在[-2，2] 上的零点个数为【　　】‎ A .2 B ‎.4 C.5 D. 8 ‎ ‎【答案】Ｂ。‎ ‎【考点】函数的周期性、奇偶性、图像及两个图像的交点问题。‎ ‎【解析】由当 且≠时 ，，知 为减函数；为增函数。‎ 又时，0＜f(x)＜1，在R上的函数f(x)是最小正周期为2的偶函数，在同一坐标系中作出和草图像如下，由图知在[-2，2] 上的零点个数为4个。‎ 例6. （2012年福建省理5分）设函数，则下列结论错误的是【 】‎ A．D(x)的值域为{0,1} B．D(x)是偶函数 C．D(x)不是周期函数 D．D(x)不是单调函数 ‎【答案】C。‎ ‎【考点】分段函数的奇偶性、单调性、值域、周期性。‎ ‎【解析】对于A选项，D(x)的值域为{0,1}，选项正确；‎ ‎ 对于B选项，∵，∴D(x)是偶函数，选项正确；‎ 对于C选项，∵，∴是D(x) 的一个周期，即D(x)是周期函数，选项错误；‎ 对于D选项，∵，但，∴D(x)不是单调函数，选项正确。‎ 故选C。‎ 例7. （2012年辽宁省文5分）函数的单调递减区间为【 】‎ ‎（A）（1,1] （B）（0,1] （C.）[1，+∞） （D）（0，+∞）‎ ‎【答案】B。‎ ‎【考点】用导数求函数的单调区间。‎ ‎【解析】∵，∴。‎ ‎ ∴。故选B。‎ 例8. （2012年辽宁省理5分）若，则下列不等式恒成立的是【 】‎ ‎(A) (B) ‎ ‎(C) (D)‎ ‎【答案】C。‎ ‎【考点】导数公式，利用导数，通过函数的单调性与最值来证明不等式。‎ ‎【解析】设，则 所以所以当时，‎ 同理∴即。故选C。‎ 例9. （2012年陕西省理5分）下列函数中，既是奇函数又是增函数的为【 】‎ A. B. C. D. ‎ ‎【答案】D。‎ ‎【考点】函数的奇偶性和增减性的判断。‎ ‎【解析】根据函数的奇偶性和增减性逐一作出判断：‎ 对于A，非奇非偶，是R上的增函数，不符合题意；‎ 对于B，是偶函数，不符合题意；‎ 对于C，是奇函数，但不是增函数；‎ 对于D，令，则 ‎∵，∴函数是奇函数；‎ ‎∵，∴函数是增函数。‎ 故选D。‎ 例10. （2012年上海市理4分）已知函数（为常数）.若在区间[1,+¥)上是增函数，则的取值范围是 ▲ .‎ ‎【答案】。‎ ‎【考点】指数函数单调性，复合函数的单调性的判断。‎ ‎【解析】根据函数看出当时函数增函数，而已知函数在区间上为增函数，所以的取值范围为： 。‎ 例11. （2012年全国课标卷文5分）设函数的最大值为M，最小值为m，则M+m= ▲ ‎ ‎【答案】2。‎ ‎【考点】奇函数的性质。‎ ‎【解析】∵， ∴设。‎ ‎ ∵，‎ ‎ ∴函数是奇函数，关于坐标原点对称，它的最大值与最小值之和为0。‎ ‎ ∴。‎ 例12. （2012年上海市理4分）已知是奇函数，且，若，则 ‎ ▲ .‎ ‎【答案】‎ ‎【考点】函数的奇偶性。‎ ‎【解析】∵函数为奇函数，∴，即 又∵，∴。∴。‎ 例13. （2012年安徽省文5分）若函数的单调递增区间是，则 ▲ [来源:学科网]‎ ‎【答案】。‎ ‎【考点】函数的单调性。‎ ‎【解析】∵，∴由对称性得，，即。‎ 例14.（2012年山东省文4分）若函数在［－1，2］上的最大值为4，最小值为m，‎ 且函数在上是增函数，则a＝ ▲ . ‎ ‎【答案】。‎ ‎【考点】函数的增减性。‎ ‎【解析】∵，∴。‎ 当时，‎ ‎∵，函数是增函数，‎ ‎∴在［－1，2］上的最大值为，最小值为。‎ 此时，它在上是减函数，与题设不符。‎ 当时，‎ ‎∵，函数是减函数，‎ ‎∴在［－1，2］上的最大值为，最小值为。‎ 此时，它在上是增函数，符合题意。‎ 综上所述，满足条件的。‎ 例15. （2012年江苏省5分）设是定义在上且周期为2的函数，在区间上，‎ 其中．若，‎ 则的值为 ▲ ．[来源:学#科#网Z#X#X#K]‎ ‎【答案】。‎ ‎【考点】周期函数的性质。‎ ‎【解析】∵是定义在上且周期为2的函数，∴，即①。‎ ‎ 又∵，，‎ ‎ ∴②。‎ ‎ 联立①②，解得，。∴。‎ 例16. （2012年浙江省文5分）设函数f（x）是定义在R上的周期为2的偶函数，当x∈[0，1]时，f（x）=x＋1，则= ▲ 。‎ ‎【答案】。‎ ‎【考点】函数的周期性和奇偶性。‎ ‎【解析】。‎ 例17.（2012年重庆市文5分）函数 为偶函数，则实数 ▲ ‎ ‎【答案】4。‎ ‎【考点】函数奇偶性的性质。‎ ‎【分析】由题意可得，对于任意的都成立，代入任一不为0的数可得关于的一元一次方程，解出即可：‎ ‎ 令，则，即，即，解得。‎ 例18. （2012年浙江省文15分）已知a∈R，函数 ‎（1）求的单调区间 ‎（2）证明：当0≤≤1时， + ＞0.‎ ‎【答案】解：（1）由题意得，‎ ‎ 当时，恒成立，此时的单调递增区间为；‎ 当时，，‎ 此时函数的单调递增区间为。‎ ‎（2）由于，当时，；‎ 当时，。[来源:Zxxk.Com]‎ 设，则。‎ 则有 ‎0‎ ‎1‎ ‎－‎ ‎－‎ ‎0‎ ‎＋‎ ‎＋‎ ‎1‎ 减 极小值 增 ‎1‎ ‎∴。‎ ‎∴当时，总有。‎ ‎∴。‎ ‎【考点】分类思想的应用，利用导数求闭区间上函数的最值和单调区间，不等式的证明。 ‎ ‎【解析】（1）求出导数，分和讨论即可。‎ ‎ （2）根据，分和两种情形，得到，从而设出新函数，应用导数，证出，得到恒成立，即。‎ 例19.（2012年江西省理14分）若函数满足 ‎（1），；‎ ‎（2）对任意，有；‎ ‎（3）在上单调递减。则称为补函数。已知函数。‎ ‎（1）判函数是否为补函数，并证明你的结论；‎ ‎（2）若存在，使得，称是函数的中介元。记时的中介元为，且，若对任意的，都有，求 的取值范围；‎ ‎（3）当，时，函数的图像总在直线的上方，求的取值范围。‎ ‎【答案】解：（1）函数h(x)是补函数，证明如下：‎ ‎①h(0)＝＝1，h(1)＝＝0；‎ ‎②对任意a∈[0,1]，有h(h(a))＝h＝＝＝a；‎ ‎③令g(x)＝(h(x))p，有g′(x)＝＝。‎ ‎∵λ>－1，p>0，∴当x∈(0,1)时，g′(x)<0。‎ ‎∴函数g(x)在(0,1)上单调递减，故函数h(x)在(0,1)上单调递减。‎ ‎（2）当p＝(n∈*)，由h(x)＝x，得λx＋2x－1＝0，(*)‎ ‎①当λ＝0时，中介元xn＝n；‎ ‎②当λ>－1且λ≠0时，由(*)得x＝∈(0,1)或x＝∉[0,1]；‎ 得中介元xn＝n。‎ 综合① ②：对任意的λ>－1，中介元为xn＝n(n∈*)。‎ ‎∴当λ>－1时，有Sn＝ i＝<，‎ 当n无限增大时，n无限接近于0，Sn无限接近于。‎ ‎∴对任意的n∈*，Sn<成立等价于≤，即λ∈[3，＋∞)．‎ ‎（3）当λ＝0时，h(x)＝(1－xp)，中介元为xp＝。‎ ‎①当01时，依题意只需(1－xp)>1－x在x∈(0,1)时恒成立，也即xp＋(1－x)p<1在x∈(0,1)时恒成立。‎ 设φ(x)＝xp＋(1－x)p，x∈(0,1)，则φ′(x)＝p[xp－1－(1－x)p－1]。‎ 由φ′(x)＝0得x＝，且当x∈时，φ′(x)<0，当x∈时，φ′(x)>0。‎ 又∵φ(0)＝φ(1)＝1，∴当x∈(0,1)时，φ(x)<1恒成立。‎ 综上：p的取值范围是(1，＋∞)。‎ ‎【考点】综合法与分析法的应用，简单的演绎推理。[来源:学科网ZXXK]‎ ‎【解析】（1）可通过对函数进行研究，探究其是否满足补函数的三个条件来确定函数是否是补函数。‎ ‎（2）由题意，先根据中介元的定义得出中介元xn通式，代入，计算出和，然后结合极限的思想，利用Sn<得到参数的不等式，解出它的取值范围。‎ ‎（3），时，对参数p分别讨论由函数的图象总在直线的上方这一位置关系进行转化，解出p的取值范围。‎