高中数学常见题型解法归纳及反馈检测 第2讲 函数的值域（最值）常见求法2

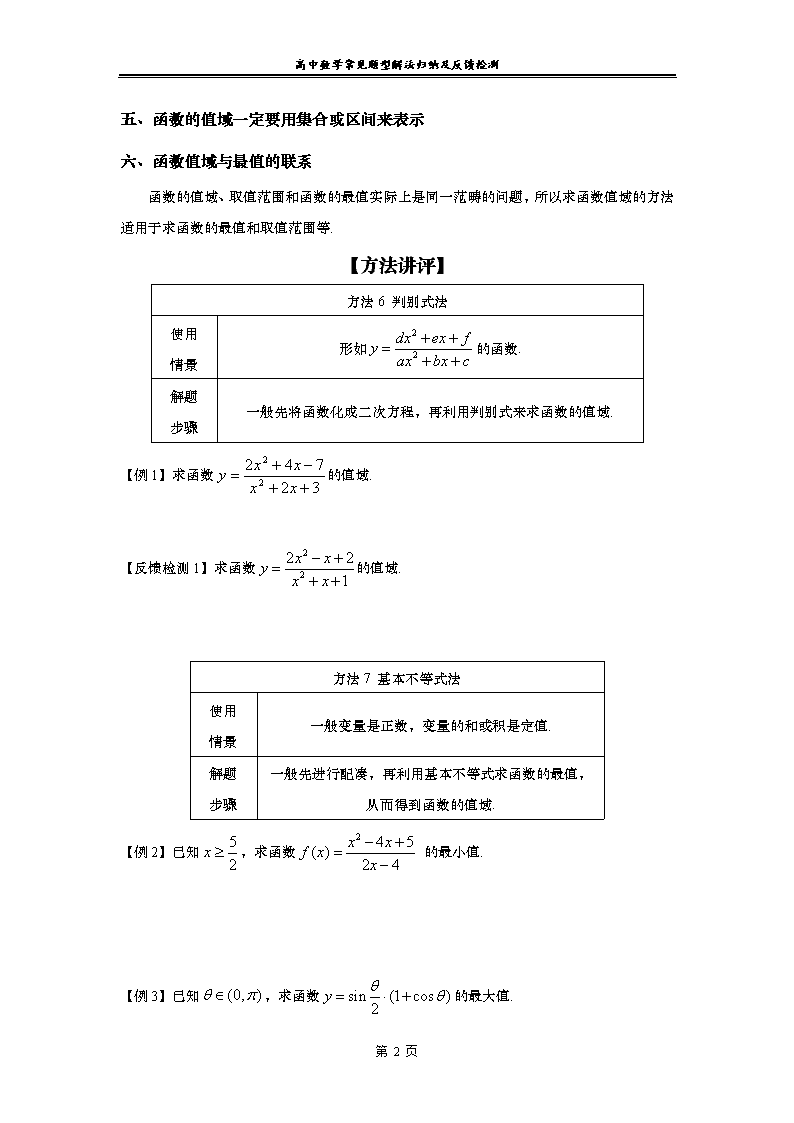
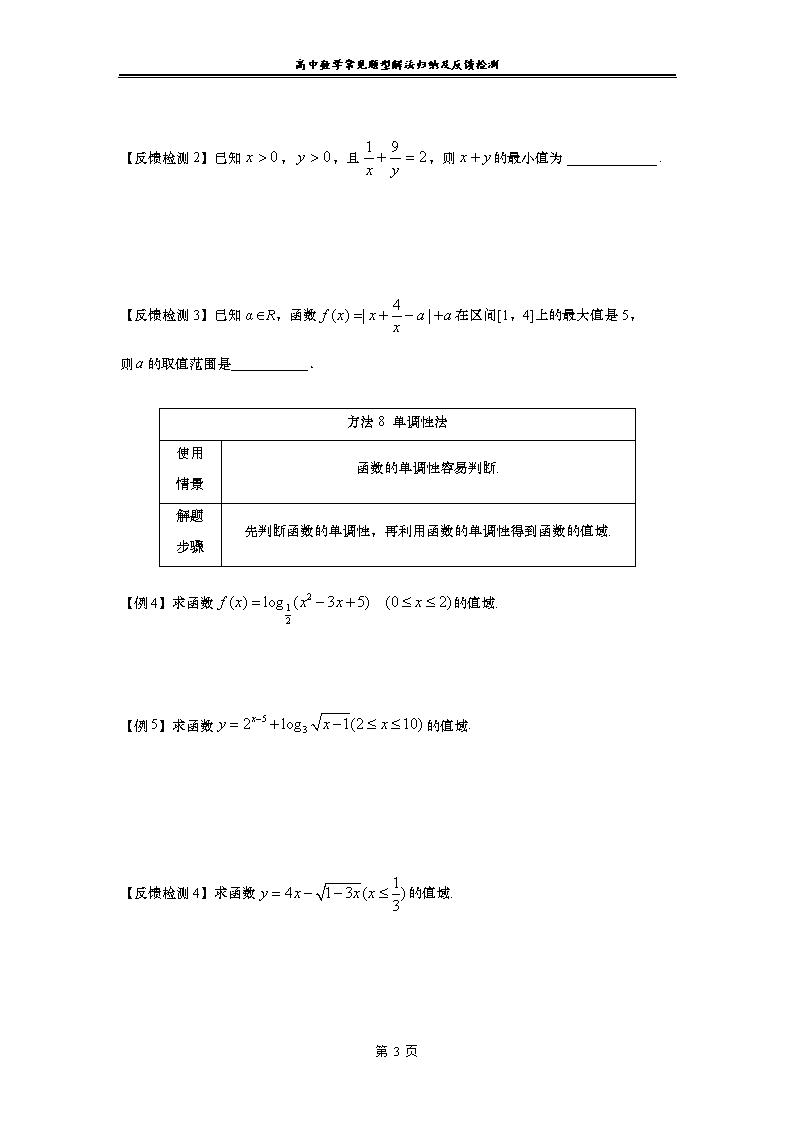
高中数学常见题型解法归纳及反馈检测 第2讲 函数的值域（最值）常见求法2

高中数学常见题型解法归纳及反馈检测 第2讲 函数的值域（最值）常见求法2‎ ‎【知识要点】‎ 一、函数值域的定义 函数值的集合叫做函数的值域.‎ 二、值域范围的决定因素 函数的值域取决于定义域和对应法则，不论采用什么方法求函数的值域，都要考虑定义域，函数的问题必须遵循“定义域优先”的原则.‎ 三、常见函数的值域 ‎1、一次函数的值域为.‎ ‎2、二次函数，当时的值域为，‎ 时的值域为.‎ ‎3、反比例函数的值域为.‎ ‎4、指数函数的值域为.‎ ‎5、对数函数的值域为. ‎ ‎6、幂函数的值域为，幂函数的值域为.‎ ‎7、正弦函数、余弦函数的值域为，正切函数的值域为.‎ 四、求函数的值域常用的方法 求函数的值域常用的方法有观察法、分离常数法、配方法、反函数法、换元法、判别式 法、基本不等式法、单调性法、数形结合法、导数法、绝对值不等式法和柯西不等式法等.其中最常用的有“三数（函数、数形结合、导数）”和“三不（基本不等式、绝对值不等式、柯西不等式）”.‎ 第 6 页 高中数学常见题型解法归纳及反馈检测 五、函数的值域一定要用集合或区间来表示 六、函数值域与最值的联系 函数的值域、取值范围和函数的最值实际上是同一范畴的问题，所以求函数值域的方法适用于求函数的最值和取值范围等.‎ ‎【方法讲评】‎ 方法6 判别式法 使用 情景 形如的函数.‎ 解题 步骤 一般先将函数化成二次方程，再利用判别式来求函数的值域.‎ ‎【例1】求函数的值域.‎ ‎【反馈检测1】求函数的值域.‎ ‎ ‎ 方法7 基本不等式法 使用 情景 一般变量是正数，变量的和或积是定值.‎ 解题 步骤 一般先进行配凑，再利用基本不等式求函数的最值，‎ 从而得到函数的值域.‎ ‎【例2】已知，求函数 的最小值.‎ ‎【例3】已知，求函数的最大值.‎ 第 6 页 高中数学常见题型解法归纳及反馈检测 ‎【反馈检测2】已知，，且，则的最小值为.‎ ‎【反馈检测3】已知αR，函数在区间[1，4]上的最大值是5，‎ 则的取值范围是___________． ‎ 方法8 单调性法 使用 情景 函数的单调性容易判断.‎ 解题 步骤 先判断函数的单调性，再利用函数的单调性得到函数的值域.‎ ‎【例4】求函数的值域.‎ ‎【例5】求函数的值域.‎ ‎【反馈检测4】求函数的值域.‎ 第 6 页 高中数学常见题型解法归纳及反馈检测 方法9 数形结合法 使用 情景 函数有明显的几何意义.‎ 解题 步骤 先找到“数”对应的“形”，再利用数形结合分析解答.‎ ‎【例6】求函数的值域.‎ ‎【例7】 如果函数定义在区间上，求的最小值.‎ ‎【例8】求函数的值域.‎ ‎【例9】设是上的偶函数，对任意，都有且当时，内关于的方程恰有3个不同的实数根，则的取值范围是（ ）‎ A．（1，2） B． C． D．‎ ‎【例10】点为抛物线：上一动点，定点，则与到轴的距离之和的最小值为（ ）‎ 第 6 页 高中数学常见题型解法归纳及反馈检测 A.9 B.10 C.8 D.5‎ ‎【例11】已知x，y满足约束条件 ‎(1)求目标函数的最大值和最小值；‎ ‎(2)若目标函数取得最大值的最优解有无穷多个，求的值；‎ ‎(3)求的取值范围．‎ ‎【反馈检测5】若点的坐标为（3，2），为抛物线的焦点，点是抛物线上的一动点，则取得最小值时，点的坐标是 .‎ A V C B ‎【例12】圆锥的底面直径，母线长，点在母线上，且，‎ 有一只蚂蚁沿圆锥的侧面从点到达点，则这只蚂蚁爬行的最短距离是（ ）‎ A． B． ‎ C． D． ‎ ‎【反馈检测6】如图，圆锥的底面圆直径为2，母线长为4，若小虫从点开始绕着圆锥表面爬行一圈到的中点，则小虫爬行的最短距离为______．‎ 第 6 页 高中数学常见题型解法归纳及反馈检测 方法10 导数法 使用 情景 函数的结构比较复杂，利用导数可以方便地求出函数的单调性.‎ 解题 步骤 先利用导数求出函数的单调性，再根据函数的单调性得到函数的值域.‎ ‎【例12】已知函数，‎ ‎（1）当时，求函数在处的切线方程；‎ ‎（2）求在区间上的最小值．‎ ‎【例13】两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为xkm，建在C处的垃圾处理厂对城A和城B的总影响度为y，统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k，当垃圾处理厂建在的中点时，对城A和城B的总影响度为0.065.‎ ‎（1）将表示成的函数；‎ ‎（2）讨论（1）中函数的单调性，并判断弧上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离;若不存在，说明理由.‎ 第 6 页