【数学】2018届一轮复习人教A版第六章 不等ʽ学案
第六章 不 等 式)
第1课时 一元二次不等式及其解法(对应学生用书(文)、(理)93~94页)
掌握一元二次不等式解法,理解一元二次不等式、一元二次方程、二次函数之间关系并能灵活运用.
① 会从实际情境中抽象出一元二次不等式模型.
② 通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.
③ 会解一元二次不等式,对给定的一元二次不等式,会设计求解程序框图.
1. (必修5P77练习2(2)改编)不等式3x2-x-4≤0的解集是__________.
答案:
解析:由3x2-x-4≤0,得(3x-4)(x+1)≤0,解得-1≤x≤.
2. (必修5P75例1(1)改编)不等式2x2-x-1>0的解集是________.
答案:∪(1,+∞)
解析:∵ 2x2-x-1>0,∴ (2x+1)(x-1)>0,∴ x>1或x<-.
3. (必修5P79习题1(3)改编)不等式8x-1≤16x2的解集是________.
答案:R
解析:原不等式转化为16x2-8x+1≥0,即(4x-1)2≥0,则x∈R,故不等式的解集为R.
4. (必修5P80习题9改编)已知不等式x2-2x+k2-3>0对一切实数x恒成立,则实数k的取值范围是________.
答案:k>2或k<-2
解析:由Δ=4-4(k2-3)<0,解得k>2或k<-2.
5. (必修5P80习题8(2)改编)关于x的不等式x2+(a+1)x+ab>0的解集是{x|x<-1或x>4},则a+b=________.
答案:-3
解析:由题意知,-1,4为方程x2+(a+1)x+ab=0的两根,∴ a+1=-3,ab=-4.∴ a=-4,b=1.∴ a+b=-3.
1. 一元二次不等式的解法
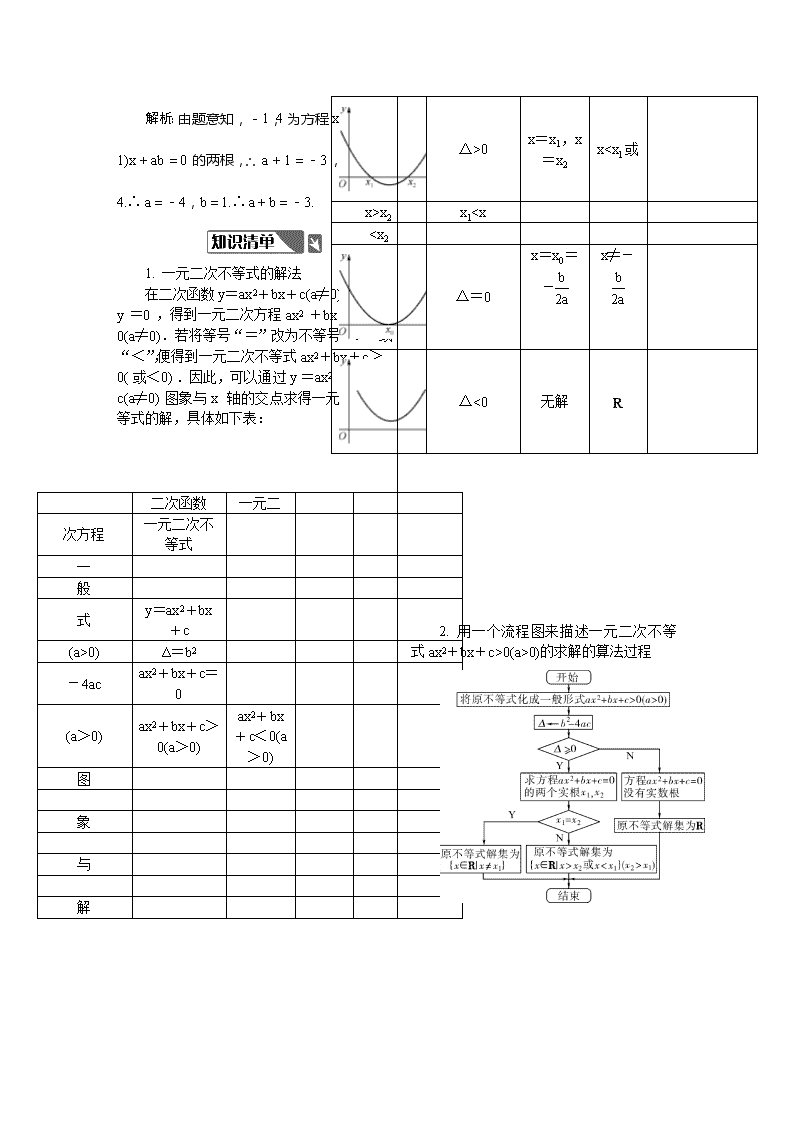
在二次函数y=ax2+bx+c(a≠0)中,令y=0,得到一元二次方程ax2+bx+c=0(a≠0).若将等号“=”改为不等号“>”或“<”,便得到一元二次不等式ax2+bx+c>0(或<0).因此,可以通过y=ax2+bx+c(a≠0)图象与x轴的交点求得一元二次不等式的解,具体如下表:
二次函数
一元二
次方程
一元二次不等式
一
般
式
y=ax2
+bx+c
(a>0)
Δ=b2
-4ac
ax2+bx+c=0
(a>0)
ax2+bx+c>0(a>0)
ax2+bx+c<0(a>0)
图
象
与
解
Δ>0
x=x1,x=x2
x
x2
x10(a>0)的求解的算法过程
, 1 一元二次不等式的解法)
, 1) 解关于x的不等式:x2-(a+1)x+a<0.
解:由x2-(a+1)x+a=0得(x-a)(x-1)=0,
∴ x1=a,x2=1,
① 当a>1时,x2-(a+1)x+a<0的解集为{x|11.
若a<0,原不等式等价于(x-1)>0,解得x<或x>1.
若a>0,原不等式等价于(x-1)<0.
①当a=1时,=1,(x-1)<0无解;
②当a>1时,<1,解(x-1)<0得1,解(x-1)<0得11};
当a=0时,解集为{x|x>1};当01时,解集为{x|0时,g(x)在[1,3]上是增函数,
所以g(x)max=g(3)7m-6<0,
所以m<,所以00,
因为m(x2-x+1)-6<0,所以m<.
因为函数y==在[1,3]上的最小值为,所以只需m<即可.
所以,m的取值范围是.
变式训练
(1) 设f(x)=mx2-mx-1,求使f(x)<0,且|m|≤1恒成立的x的取值范围;
(2) 已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.
解:(1) 将不等式f(x)<0整理成关于m的不等式为(x2-x)m-1<0.令g(m)=(x2-x)m-1,m∈[-1,1].
则即
解得<x<,
即x的取值范围是.
(2) (解法1)f(x)=(x-a)2+2-a2,此二次函数图象的对称轴为x=a.
① 当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,f(x)min=f(-1)=2a+3.要使f(x)≥a恒成立,只需f(x)min≥a,即2a+3≥a,
解得-3≤a<-1;
② 当a∈[-1,+∞)时,f(x)min=f(a)=2-a2,
由2-a2≥a,解得-1≤a≤1.
综上所述,所求a的取值范围是[-3,1].
(解法2)令g(x)=x2-2ax+2-a,由已知,得x2-2ax+2-a≥0在[-1,+∞)上恒成立,
即Δ=4a2-4(2-a)≤0或
解得-3≤a≤1,所以a的取值范围是[-3,1].
, 3 三个二次之间的关系)
, 3) (1) 已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞).若关于x的不等式f(x)0恒成立,则实数a的取值范围是_________.
答案:(1) 9 (2) {a|a>-3}
解析:(1) 由题意知f(x)=x2+ax+b=+b-.
∵ f(x)的值域为[0,+∞),
∴ b-=0,即b=.
∴ f(x)=.
∵ f(x)0恒成立,即x2+2x+a>0恒成立.
即当x≥1时,a>-(x2+2x)=g(x)恒成立.
而g(x)=-(x2+2x)=-(x+1)2+1在[1,+∞)上单调递减,
∴ g(x)max=g(1)=-3,故a>-3.
∴ 实数a的取值范围是{a|a>-3}.
关于x的不等式x2-(a+1)x+a<0的解集中,恰有3个整数,求a的取值范围.
解:原不等式可能为(x-1)(x-a)<0,当a>1时得1<x<a,此时解集中的整数为2,3,4,则4<a≤5,当a<1时得a<x<1,则-3≤a<-2,故a∈[-3,-2)∪(4,5].
, 4 一元二次不等式的应用)
, 4) 一个服装厂生产风衣,月销售量x(件)与售价p(元/件)之间的关系为p=160-2x,生产x件的成本R=500+30x(元).
(1) 该厂月产量多大时,月利润不少于1 300元?
(2) 当月产量为多少时,可获得最大利润,最大利润是多少?
解:(1) 由题意知,月利润y=px-R,即y=(160-2x)x-(500+30x)=-2x2+130x-500.
由月利润不少于1 300元,得-2x2+130x-500≥1 300.即x2-65x+900≤0,解得20≤x≤45.故该厂月产量在20~45件时,月利润不少于1 300元.
(2) 由(1)得,y=-2x2+130x-500=-2+,
由题意知,x为正整数.故当x=32或33时,y最大为1 612.
所以当月产量为32或33件时,可获最大利润,最大利润为1 612元.
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:R(x)=假定该产品产销平衡,那么根据上述统计规律求下列问题.
(1) 要使工厂有赢利,产量x应控制在什么范围内?
(2) 工厂生产多少台产品时,可使赢利最多?
解:依题意,G(x)=x+2,设利润函数为f(x),则
f(x)=
(1) 要使工厂有赢利,即解不等式f(x)>0,
当0≤x≤5时,解不等式-0.4x2+3.2x-2.8>0,
即x2-8x+7<0,得15时,解不等式8.2-x>0,得 x<8.2,∴ 55时,f(x)<8.2-5=3.2.
所以,当工厂生产400台产品时,赢利最多.
1. 不等式-x2-3x+4>0的解集为____________.(用区间表示)
答案:(-4,1)
解析:由-x2-3x+4>0,得-4x1时,不符合任意正数t都满足;当-20,ax2+bx+c<0的解就是使二次函数y=ax2+bx+c的函数值大于0或小于0时x的范围,应充分和二次函数图象结合去理解一元二次不等式的解集表.
2. 解含参数的不等式(x-a)(x-b)>0,应讨论a与b的大小再确定不等式的解,解一元二次不等式的一般过程是:一看(看二次项系数的符号),二算(计算判别式,判断方程的根的情况),三写(写出不等式的解集).
3. 应注意讨论ax2+bx+c>0的二次项系数a是否为0.
4. 要注意体会数形结合与分类讨论的数学思想.分类讨论要做到“不重”、“不漏”、“最简”的三原则.
[备课札记]
第2课时 二元一次不等式(组)与
简单的线性规划(对应学生用书(文)、(理)95~96页)
会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
① 会从实际情境中抽象出二元一次不等式组.② 了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.③ 会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
1. (必修5P83练习1改编)若点P(a,3)在2x+y<3表示的区域内,则实数a的取值范围是________.
答案:a<0
解析:点P(a,3)在2x+y<3表示的区域内,则2a+3<3,解得a<0.
2. (必修5P86练习2(1)改编)不等式组所表示的平面区域的面积是________.
答案:25
解析:直线x-y+4=0与直线x+y=0的交点为A(-2,2),直线x-y+4=0与直线x=3的交点为B(3,7),直线x+y=0与直线x=3的交点为C(3,-3),则不等式组表示的平面区域是一个以点A(-2,2),B(3,7),C(3,-3)为顶点的三角形,所以其面积为S△ABC=×5×10=25.
3. 设实数x,y满足则z=3x+2y的最大值是________.
答案:7
解析:由题设可知可行域的四个顶点坐标分别为(0,0),(2,0),(0,3),(1,2).因此(3x+2y)max=3×1+2×2=7.
4. (必修5P34练习7改编)设变量x,y满足约束条件:则z=x-3y的最小值为________.
答案:-8
解析:画出可行域与目标函数线,如图可知,目标函数在点(-2,2)处取最小值-8.
5. 已知实数x,y满足不等式组则z=2x-y的最大值为________.
答案:8
解析:画出可行域,如图中阴影部分所示.由图可知z=2x-y在点A(4,0)处取最大值,即zmax=8.
1. 二元一次不等式(组)表示的平面区域
(1) 二元一次不等式表示的平面区域
一般地,直线y=kx+b把平面分成两个区域,
y>kx+b表示直线y=kx+b上方的平面区域,
y0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为________.
答案:4
解析:画出约束条件表示的可行域(如图所示).当目标函数z=ax+by过点A(2,1)时,z取得最小值,即2=2a+b,所以2-2a=b,所以a2+b2=a2+(2-2a)2=5a2-8a+20,构造函数m(a)=5a2-8a+20(>a>0),利用二次函数求最值,函数m(a)=5a2-8a+20的最小值是=4,即a2+b2的最小值为4.
3. 已知变量x,y满足约束条件且有无穷多个点(x,y)使目标函数z=x+my取得最小值,则m=________.
答案:1
解析:作出线性约束条件表示的平面区域,如图阴影部分所示.
若m=0,则z=x,目标函数z=x+my取得最小值的最优解只有一个,不符合题意;若m≠0,则目标函数z=x+my可
看作斜率为-的动直线y=-x+.
若m<0,则->0,数形结合知使目标函数z=x+my取得最小值的最优解不可能有无穷多个;
若m>0,则-<0,数形结合可知,当动直线与直线AB重合时,有无穷多个点(x,y)在线段AB上,使目标函数z=x+my取得最小值,即-=-1,则m=1.
综上可知,m=1.
4. 若实数x,y满足x2+y2≤1,则|2x+y-2|+|6-x-3y|的最小值是________.
答案:3
解析:满足x2+y2≤1的实数x,y表示的点(x,y)构成的区域是单位圆及其内部.
f(x,y)=|2x+y-2|+|6-x-3y|
=|2x+y-2|+6-x-3y
=
直线y=-2x+2与圆x2+y2=1交于A,B两点,如图所示,易得B.
设z1=4+x-2y,z2=8-3x-4y,分别作直线y=x和y=-x并平移,则z1=4+x-2y在点B取得最小值为3,z2
=8-3x-4y在点B取得最小值为3,所以|2x+y-2|+|6-x-3y|的最小值是3.
1. 确定不等式Ax+By+C>0(<0,≥0,≤0)表示直线Ax+By+C=0的哪一侧区域,常用两种方法:一是在直线的某一侧取一特殊点;二是将不等式化为y>kx+b(<,≥,≤).
2. 在线性约束条件下,当b>0时,求目标函数z=ax+by+c的最值的求解步骤
(1) 作出可行域;
(2) 作出直线l0:ax+by=0;
(3) 平移直线l0:ax+by=0,依可行域判断取得最值的最优解的点;
(4) 解相关方程组,求出最优解,从而得出目标函数的最值.
3. 常见的非线性目标函数的几何意义
(1) 表示点(x,y)与原点(0,0)的距离;
(2) 表示点(x,y)与点(a,b)的距离;
(3) 表示点(x,y)与原点(0,0)连线的斜率值;
(4) 表示点(x,y)与点(a,b)连线的斜率值.
[备课札记]
第3课时 基本不等式(对应学生用书(文)、(理)97~98页)
掌握基本不等式,能利用基本不等式推导不等式,能利用基本不等式求最大(小)值.
① 了解基本不等式的证明过程.② 会用基本不等式解决简单的最大(小)值问题.
1. (必修5P99练习4改编)若实数a,b满足a+b=2,则3a+3b的最小值是________.
答案:6
解析:由基本不等式,得3a+3b≥2=2=6,当且仅当a=b=1时取等号,所以3a+3b的最小值是6.
2. (必修5P105复习题9改编)若f(x)=x+-2(x<0),则f(x)的最大值为________.
答案:-4
解析:∵ x<0,∴ f(x)=-[(-x)+]-2≤-2-2=-4,当且仅当-x=,即x=-1时取等号.
3. (必修5P105复习题10改编)若x>-3,则x+的最小值为________.
答案:2-3
解析:∵ x+3>0,∴ x+=(x+3)+-3≥2-3=2-3.
4. (必修5P107测试3改编)对任意x>0,≤a恒成立,则实数a的取值范围是________.
答案:
解析:因为≤a恒成立,所以a≥.
又=≤=,当且仅当x=时等号成立,所以a≥.
5. (必修5P106复习题10改编)已知a>0,b>0,若不等式+≥恒成立,则m的最大值等于________.
答案:9
解析:原不等式恒成立等价于m≤(2a+b)的最小值,而(2a+b)=5++≥5+2=9,所以m≤9,即m的最大值为9.
1. 算术平均数与几何平均数
对于正数a,b,我们把称为a,b的算术平均数,称为a,b的几何平均数.
2. 基本不等式≤
(1) 基本不等式成立的条件:a≥0,b≥0;
(2) 等号成立的条件:当且仅当a=b时取等号;
(3) 结论:两个非负数a,b的算术平均数不小于其几何平均数.
3. 拓展:若a>0,b>0,≤≤≤,当且仅当a=b时等号成立.
[备课札记]
, 1 通过配凑法利用基本不等式求最值)
, 1) (1) 已知x<,则f(x)=4x-2+的最大值为________;
(2) 若函数f(x)=x+(x>2)在x=a处取最小值,则a=________.
答案:(1) 1 (2) 3
解析:(1) 因为x<,所以5-4x>0,则f(x)=4x-2+=-+3≤-2+3=1.
当且仅当5-4x=,即x=1时,等号成立.
故f(x)=4x-2+的最大值为1.
(2) 因为x>2,所以x-2>0,则f(x)=x+=(x-2)++2≥2+2=4,当且仅当x-2=,即x=3时取等号.
所以当f(x)取得最小值时,x=3,即a=3.
正数x,y满足+=1.
(1) 求xy的最小值;
(2) 求x+2y的最小值.
解:(1) 由1=+≥2得xy≥36,当且仅当=,即y=9x=18时取等号,故xy的最小值为36.
(2) 由题意可得x+2y=(x+2y)=19++≥19+2=19+6,当且仅当=,即9x2=2y2时取等号,故x+2y的最小值为19+6.
, 2 通过常数代换或消元法利用基本不等式求最值)
, 2) (1) 已知x>0,y>0且x+y=1,则+的最小值为________;
(2) 已知x>0,y>0,x+3y+xy=9,则x+3y的最小值为________.
答案:(1) 18 (2) 6[来源:学§科§网Z§X§X§K]
解析:(1) (常数代换法)
∵ x>0,y>0,且x+y=1,∴ +=(x+y)=10++≥10+2=18.
当且仅当=,即x=2y时等号成立,
∴ 当x=,y=时,+有最小值18.
(2) 由已知得x=.
(解法1:消元法)
∵ x>0,y>0,∴ y<3,∴ x+3y=+3y
=+(3y+3)-6≥2-6=6,
当且仅当=3y+3,即y=1,x=3时,(x+3y)min=6.
(解法2)∵ x>0,y>0,9-(x+3y)=xy=
x·(3y)≤·,
当且仅当x=3y时等号成立.
设x+3y=t>0,则t2+12t-108≥0,
∴ (t-6)(t+18)≥0.
又t>0,∴ t≥6.
故当x=3,y=1时,(x+3y)min=6.
变式训练
(1) 已知x,y∈(0,+∞),2x-3=,若+(m>0)的最小值为3,则m=________;
(2) 已知正数x,y满足x+2y=2,则的最小值为__________.
答案:(1) 4 (2) 9
解析:(1) 由2x-3=得x+y=3,+=(x+y)·=≥(1+m+2)(当且仅当=时取等号),∴ (1+m+2)=3,解得m=4.
(2) 因为x,y为正数,且x+2y=2,==++5≥2 +5=9,当且仅当x=4y=时,等号成立,所以的最小值为9.
, 3 基本不等式与函数的综合应用)
, 3) 已知函数f(x)=(a∈R),若对于任意x∈N*,f(x)≥3恒成立,则a的取值范围是________.
答案:
解析:对任意x∈N*,f(x)≥3恒成立,即≥3恒成立,可得
a≥-+3.
设g(x)=x+,x∈N*,
∵ g(x)在(0,2]上单调递减,在[2,+∞)上单调递增,而x∈N*,∴ g(x)在x取距离2较近的整数值时达到最小,而距离2较近的整数为2和3,且g(2)=6,g(3)=.
∵ g(2)>g(3),∴ g(x)min=.
∴ -+3≤-,[来源:Z。xx。k.Com]
∴ a≥-,故a的取值范围是.
变式训练
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中四边形ABCD是一个矩形,四边形EFCD是一个等腰梯形,梯形高h=AB,tan∠FED=,设AB=x m,BC=y m.
(1) 求y关于x的表达式;
(2) 怎样设计x,y的长度,才能使所用材料最少?
解:(1) 如图,作DH⊥EF于点H.
依题意,DH=AB=x,
EH==×x=x,
∴ =xy+x=xy+x2,
∴ y=-x.
∵ x>0,y>0,
∴ -x>0,解得0<x<,
∴ 所求表达式为y=-x.
(2) 在Rt△DEH中,∵ tan ∠FED=,∴ sin ∠FED=,
∴ DE==x×=x,
∴ l=(2x+2y)+2×x+
=2y+6x=-x+6x
=+x≥2 =26.
当且仅当=x,即x2=9,x=3时取等号,此时y=-x=4,
∴ AB=3 m,BC=4 m时,能使整个框架用材料最少.
, 4 基本不等式的实际应用)
, 4) 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30 m,其中大圆弧所在圆的半径为10 m.设小圆弧所在圆的半径为x m,圆心角为θ(弧度).
(1) 求θ关于x的函数关系式;
(2) 已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y,求y关于x的函数关系式,并求出x为何值时,y取得最大值?
解:(1) 由题意可得,30=θ(10+x)+2(10-x),所以θ=(0<x<10).
(2) 花坛的面积为θ(102-x2)=(5+x)(10-x)=-x2+5x+50(0<x<10).
装饰总费用为9θ(10+x)+8(10-x)=170+10x,所以花坛的面积与装饰总费用的比y==-.令t=17+x,则y=-≤,当且仅当t=18时取等号,此时x=1,θ=.
所以当x=1时,花坛的面积与装饰总费用的比最大.
如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为90°.已知OC=4 km,OC与公路l1夹角为60°.现规划在公路l1,l2上分别选择A,B两处作为交汇点(异于点O)直接修建一条公路通过C城,设OA=x km,OB=y km.
(1) 求出y关于x的函数关系式并指出它的定义域;
(2) 试确定点A,B的位置,使△AOB的面积最小.
解:(1) ∵ S△AOC+S△BOC=S△AOB,
∴ x·4sin60°+y·4sin30°=xy,整理得
y=,
过C作OB平行线与OA交于D,OA>OD,故x>2.定义域为{x|x>2}.
(2) S△AOB=xy=(x>2),
S△AOB==
=.
∵ x-2>0,∴ x-2+≥4,当且仅当2=4即x=4时取等号.
所以当x=4时,S△AOB有最小值为8.
答:当OA=4 km,OB=4 km时,使△AOB的面积最小.
1. 已知常数a>0,函数f(x)=x+(x>1)的最小值为3,则a的值为________.
答案:1
解析:f(x)=x-1++1≥2+1=3,则a=1.
2. 若实数x,y满足x>y>0,且log2x+log2y=1,则的最小值为________.
答案:4
解析:由log2x+log2y=1,得xy=2,===x-y+≥4,则的最小值为4.
3. (2016·苏北四市三模)已知对满足x+y+4=2xy的任意正实数x,y,都有x2+2xy+y2-ax-ay+1≥0,则实数a的取值范围是____________.
答案:
解析:x+y+4=2xy≤2×,解得x+y≥4,当且仅当x=y=2时取“=”.
∵ (x+y)2-a(x+y)+1≥0,∴ (x+y)+≥a.
∵ (x+y)+≥,则a≤.
4. (2016·镇江期末)函数y=asin(ax+θ)(a>0,θ≠0)图象上的一个最高点和其相邻最低点的距离的最小值为__________.
答案:2
解析:函数的周期T为,则=,最高点和其相邻最低点的距离为2=≥=2.
5. (2016·江苏卷)在锐角三角形ABC中,若sin A=2sin Bsin C,则tan Atan Btan C的最小值是__________.
答案:8
解析:(解法1)∵ sin A=2sin Bsin C,sin A=sin(B+C)=sin Bcos C+cos Bsin C,
∴ sin Bcos C+cos Bsin C=2sin Bsin C,
两边同除以cos Bcos C,可得tan B+tan C=2tan Btan C,
tan Atan Btan C=-tan(B+C)tan Btan C=-·tan Btan C=,
由三角形为锐角三角形得tan B>0,tan C>0,tan A=>0,即tan Btan C-1>0.令tan Btan C-1=t(t>0),则tan Atan Btan C==2t++4≥8,
当t=1,即tan Btan C=2时取等号.
(解法2)同解法1可得tan B+tan C=2tan Btan C,
又tan A+tan B+tan C=tan A+(1-tan Btan C)·tan(B+C)=tan A-tan A+tan Atan Btan C=tan Atan Btan C,
∴ tan Atan Btan C=tan A+tan B+tan
C=tan A+2tan Btan C≥2tan Atan Btan C≥8,
当且仅当tan A=2tan Btan C=4时取等号.
, 7. 忽视最值取得的条件致误)
典例 (1) 已知x>0,y>0,且+=1,则x+y的最小值是________;
(2) 函数y=1-2x-(x<0)的最小值为________.
易错分析:(1) 多次使用基本不等式,忽略等号成立的条件.如:1=+≥2,∴ ≥2,∴ x+y≥2≥4,得(x+y)min=4.
(2) 没有注意到x<0这个条件,误用基本不等式得2x+≥2.
解析:(1) ∵ x>0,y>0,
∴ x+y=(x+y)=3++≥3+2(当且仅当y=x时取等号),
∴ 当x=+1,y=2+时,(x+y)min=3+2.
(2) ∵ x<0,∴ y=1-2x-=1+(-2x)+≥1+2=1+2,当且仅当x=-时取等号,故y的最小值为1+2.
答案:(1) 3+2 (2) 1+2
特别提醒:(1) 利用基本不等式求最值,一定要注意应用条件;(2) 尽量避免多次使用基本不等式,若必须多次使用,一定要保证等号成立的条件一致.
1. 已知a>0,b>0,若不等式+≥恒成立,则m的最大值为________.
答案:12
解析:由+≥得m≤(a+3b)=++6.又++6≥2+6=12,∴ m≤12,∴ m的最大值为12.
2. 已知x>0,y>0,且+=1,若x+2y>m2+2m恒成立,则实数m的取值范围是________.
答案: (-4,2)
解析:由x>0,y>0,且+=1,得x+2y=(x+2y)=4++≥4+2=8.当且仅当=时,即x=2y时取等号.又+=1,此时x=4,y=2,所以(x+2y)min=8.要使x+2y>m2+2m恒成立,只需(x+2y)min>m2+2m恒成立,即8>m2+2m,解得-4y>0,且x+y≤2,则+的最小值为________.
答案:
解析:因为x>y>0,且x+y≤2,则2x+2y≤4,+>0,所以4≥(2x+2y)=[(x+3y)+(x-y)]=2+++1≥3+2.
5. 设正项等差数列{an}的前2 011项和等于2 011,则+的最小值为________.
答案:2
解析:由题意得S2 011==2 011,
∴ a1+a2 011=2.又a2+a2 010=a1+a2 011=2,
∴ +=(a2+a2 010)=(+)+1≥2.
1. a2+b2≥2ab成立的条件是a,b∈R,而≥成立的条件是a≥0,b≥0,使用时要注意公式成立的前提条件.
2. 在运用基本不等式时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中的“一正”(即条件中字母为正数),“二定”(不等式的另一边必须为定值),“三相等”(等号取得的条件).
3. 正确理解定理:“和一定,相等时积最大;积一定,相等时和最小”.
4. 连续使用公式两次或以上,要求同时满足任何一次的字母取值存在且一致.
5. 函数y=ax+(a>0,b>0)的单调性要掌握,特别是运用基本不等式不能满足“三相等”时.
[备课札记]
第4课时 不等式的综合应用(对应学生用书(文)、(理)99~100页)
掌握不等式的综合应用;掌握基本不等式的综合应用;掌握不等式与其他函数方程等知识的综合应用.
应用性问题的基本思路:读题(背景、结论)—条件—建模—解题—反思—作答.
1. (必修5P102习题7改编)函数y=x+(x≠0)的值域是________.
答案:(-∞,-4]∪[4,+∞)
解析:当x>0时,y=x+≥2=4;当x<0时,y=x+=-≤-2=-4.
2. (必修5P102习题9改编)某种产品按下列三种方案两次提价.方案甲:第一次提价p%,第二次提价q%;方案乙:第一次提价q%,第二次提价p%;方案丙:第一次提价%,第二次提价%.其中p>q>0,上述三种方案中提价最多的是________.
答案:方案丙
解析:设原来价格为A,方案甲:经两次提价后价格为A=A;方案乙:经两次提价后价格为A;方案丙:经两次提价后价格为A=A[1++.因为>,所以方案丙提价最多.
3. 设x∈R,f(x)=,若不等式f(x)+f(2x)≤k对于任意的x∈R恒成立,则实数k的取值范围是________.
答案:k≥2
解析:不等式化为k≥+,因为∈(0,1],所以k≥2.
4. (必修5P106复习题16改编)已知x>0,y>0且满足+=1,则x+y的最小值是________ .
答案:18
解析:∵ x+y=(x+y)·1=(x+y)·=2+8++,x>0,y>0,∴ >0,>0,x+y≥10+2=18,当且仅当=时等号成立,又+=1,∴ 当x=6,y=12时,x+y有最小值18.
5. (必修5P98练习2(2)改编)若正数a,b满足ab=a+b+3,则ab的取值范围是________.
答案:[9,+∞)
解析:由a,b∈R*,得a+b≥2,则ab=a+b+3≥2+3,即ab-2-3≥0(-3)(+1)≥0≥3,∴ ab≥9.
[备课札记]
, 1 含参数的不等式问题)
, 1) 若不等式组的解集中所含整数解只有-2,求k的取值范围.
解:由x2-x-2>0有x<-1或x>2,
由2x2+(5+2k)x+5k<0有(2x+5)(x+k)<0,
因为-2是原不等式组的解,所以k<2.
由(2x+5)(x+k)<0有-<x<-k.
因为原不等式组的整数解只有-2,
所以-2<-k≤3,即-3≤k<2,
故k的取值范围是[-3,2).
变式训练
已知函数f(x)=lg[(m2-3m+2)x2+(m-1)x+1]的定义域为R,求实数m的取值范围.
解:∵ 函数f(x)的定义域为R,∴ 对于任意x∈R,恒有(m2-3m+2)x2+(m-1)x+1>0.
① 若m2-3m+2=0,则m=2或1.
当m=1时,不等式即为1>0,符合题意;
当m=2时,不等式即为x+1>0,对任意x∈R不恒成立,
∴ m=2不合题意,舍去.
② 若m2-3m+2≠0,由题意得
解得即m<1或m>.
综上可得,m的取值范围是m≤1或m>.
, 2 不等式在实际问题中的应用)
, 2) 某水库堤坝因年久失修,发生了渗水现象,经测算坝面每渗水1 m2的直接经济损失约为250元.当发现时已有200 m2的坝面渗水.且渗水还在以每天4 m2的速度扩散. 当地政府在发现的同时立即组织民工抢修,假定每位民工平均每天可抢修渗水面积2 m2,为此政府需支出服装补贴费每人400元,劳务费每人每天150元,所消耗的维修材料等费用每人每天150元.若安排x名民工参与抢修,抢修完成需用n天.
(1) 写出n关于x的函数关系式;
(2) 应安排多少名民工参与抢修,才能使总损失最小?(总损失=渗水损失+政府支出)
解:(1) 由题意得2nx=200+4n,所以n=,x≥3,x∈N*.
(2) 设总损失为y,则y=(200+4n)×250+400x+nx(150+150)=50 000+1 000n+400x+300nx=50 000+1 000·+400x+300·x=80 800+400(x-2)+≥80 800+2×20×400=96 800.
当且仅当400(x-2)=,即x=22时,等号成立.
所以应安排22名民工参与抢修,才能使总损失最小.
现有一占地1 800 m2的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1 m的赏花小径,设花圃占地面积为s m2,设矩形一边的长为x(如图所示)
(1) 试将s表示为x的函数;
(2) 问应该如何设计矩形地块的边长,使花圃占地面积s取得最大值.
解:(1) 由题知s=a(x-2)+2a(x-3)=a(3x-8),
又3a+3=,则a=-1,
所以s=(3x-8)=1 808-3x-.
(2) s=1 808-3x-=1 808-3≤1 808-240=1 568.(当且仅当x=40时取等号),此时另一边长为45 m.[来源:Zxxk.Com]
答:当x=40 m,另一边长为45 m时花圃占地面积s取得最大值1 568 m2.
, 3 基本不等式的灵活运用)
, 3) 设x,y均为正实数,且+=1,则xy的最小值为__________.
答案:16
解析:由+=1,得xy=8+x+y.
∵ x,y均为正实数,∴ xy=8+x+y≥8+2(当且仅当x=y时等号成立),即xy-2-8≥0,解得≥4,即xy≥16.故xy的最小值为16.
变式训练
设实数n≤6,若不等式2xm+(2-x)n-8≥0对任意x∈[-4,2]都成立,则的最小值为________.
答案:-
解析:设f(x)=2xm+(2-x)n-8=(2m-n)x+(2n-8)为关于x的一次函数.
由题设得即
作出不等式组所表示的可行域如图所示,
设=t,则t表示可行域内的点与坐标原点所连线段的斜率,可得≤t≤3.
g(t)==-t3在≤t≤3上为减函数,所以-≤g(t)≤-.
故的最小值为-.
1. (2016·扬州期末)已知a>b>1且2logab+3logba=7,则a+的最小值为__________.
答案:3
解析:由a>b>1,得logab<1,由2logab+3logba=7,得logab=,即b2=a,a+=a+-1+1≥2+1=3,则a+的最小值为3.
2. (2016·苏州期中)已知x+y=1,y>0,x>0,则+的最小值为________.
答案:
解析:将x+y=1代入+中,得+=++.设=t>0,则原式=+==·=[(1+2t)++1]≥×2+=,当且仅当t=时,即x=,y=时,取“=”.
3. 设Sn是等差数列{an}的前n项和.若数列{an}满足an+Sn=An2+Bn+C且A>0,则+B-C的最小值为________.
答案:2
解析:因为{an}为等差数列,设公差为d,由an+Sn=An2+Bn+C,得a1+(n-1)d+na1+n(n-1)d=an+Sn=An2+Bn+C,即(d-A)n2+n+(a1-d-C)=0对任意正整数n都成立.所以d-A=0,a1+d-B=0,a1-d-C=0,所以A=d,B=a1+d,C=a1-d,所以3A-B+C=0,则+B-C=+3A≥2.
4. (2016·南通二模)设实数x,y满足-y2=1,则3x2-2xy的最小值是________.
答案:4+6
解析:由-y2=1,得=1.假设-y=m,+y=n,即mn=1,则x=m+n,y=.所以3x2-2xy=4m2+2n2+6mn≥2+6mn=4+6(当且仅当4m2=2n2时取等号).
5. 设数列{an}的前n项和为Sn,且an=4+.若对任意n∈N*,都有1≤p(Sn-4n)≤3,则实数p的取值范围是________.
答案:[2,3]
解析:Sn=4n+,可得1≤[1-(-)n]p≤3,即1≤[1-(-)n]min且max≤3,前者n=2,后者n=1,解得2≤p≤3.
1. 已知a,b为正数,且直线ax+by-6=0与直线2x+(b-3)y+5=0互相平行,则2a+3b的最小值为________.
答案:25
解析:由直线平行可得2b=a(b-3),即3a+2b=ab,则+=1,(2a+3b)=4+9+6≥25,则2a+3b的最小值为25.
2. 在等差数列{an}中,已知首项a1>0,公差d>0.若a1+a2≤60,a2+a3≤100,则5a1+a5的最大值为________.
答案:200
解析:由a1+a2≤60,a2+a3≤100得2a1+d≤60,2a1+3d≤100,a1>0, d>0. 由线性规划的知识得5a1+a5=6a1+4d,过点(20,20)时,取最大值为200.
3. 已知正实数a,b满足9a2+b2=1,则的最大值为________.
答案:
解析:设3a=cos θ,b=sin θ,其中θ为锐角,=
;设t=sin θ+cos θ,θ为锐角,则1
查看更多