2018届二轮复习（理）规范答题示例8　直线与圆锥曲线的位置关系课件（全国通用）

2018届二轮复习（理）规范答题示例8　直线与圆锥曲线的位置关系课件（全国通用）

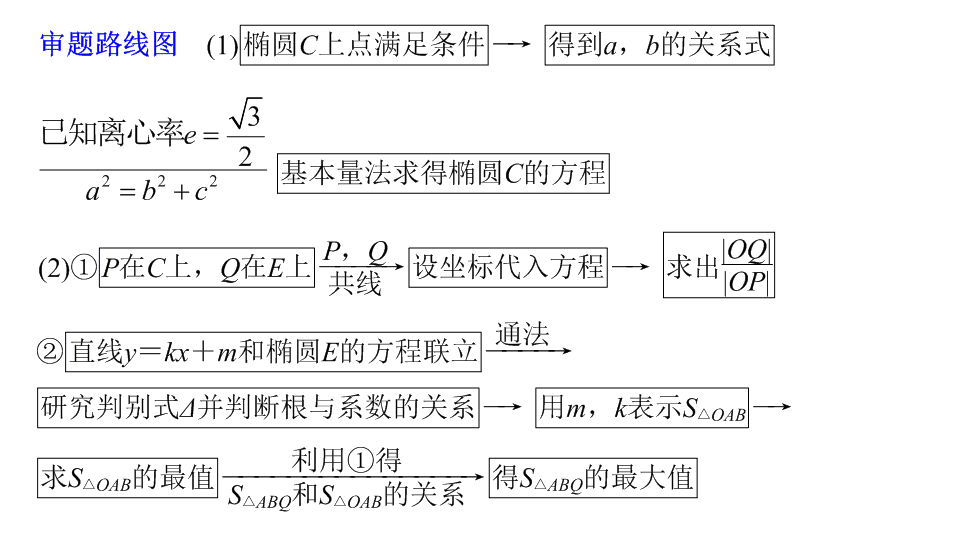
规范答题 示例 8 　 直线与圆锥曲线的位置关系 规 范 解 答 · 分 步 得 分 ② 设 A ( x 1 ， y 1 ) ， B ( x 2 ， y 2 ). 将 y ＝ kx ＋ m 代入椭圆 E 的方程，可得 (1 ＋ 4 k 2 ) x 2 ＋ 8 kmx ＋ 4 m 2 － 16 ＝ 0 ， 由 Δ ＞ 0 ，可得 m 2 ＜ 4 ＋ 16 k 2 ， (*) 因为直线 y ＝ kx ＋ m 与 y 轴交点的坐标为 (0 ， m ) ， 可得 (1 ＋ 4 k 2 ) x 2 ＋ 8 kmx ＋ 4 m 2 － 4 ＝ 0 ， 由 Δ ≥ 0 ，可得 m 2 ≤ 1 ＋ 4 k 2 . (**) 构 建 答 题 模 板 第一步 求圆锥曲线方程： 根据基本量法确定圆锥曲线的方程 . 第二步 联立消元： 将直线方程和圆锥曲线方程联立得到方程： Ax 2 ＋ Bx ＋ C ＝ 0 ，然后研究判别式，利用根与系数的关系 . 第三步 找关系： 从题设中寻求变量的等量或不等关系 . 第四步 建函数： 对范围最值类问题，要建立关于目标变量的函数关系 . 第五步 得范围： 通过求解函数值域或解不等式得目标变量的范围或最值，要注意变量条件的制约，检查最值取得的条件 . 评分细则　 (1) 第 (1) 问中，求 a 2 － c 2 ＝ b 2 关系式直接得 b ＝ 1 ，扣 1 分； (2) 第 (2) 问中， 求 时 ，给出 P ， Q 的坐标关系给 1 分；无 “ Δ >0 ” 和 “ Δ ≥ 0 ” 者，每处扣 1 分；联立方程消元得出关于 x 的一元二次方程 给 1 分；根与系数的关系写出后再给 1 分；求最值时，不指明最值取得的条件扣 1 分 . 解答 (1) 求 C 的方程； 解　 由于 P 3 ， P 4 两点关于 y 轴对称 ， 故 由题设知椭圆 C 经过 P 3 ， P 4 两点 . 所以点 P 2 在椭圆 C 上 . 证明 (2) 设直线 l 不经过 P 2 点且与 C 相交于 A ， B 两点 . 若直线 P 2 A 与直线 P 2 B 的斜率的和为－ 1 ，证明： l 过定点 . 证明　 设直线 P 2 A 与直线 P 2 B 的斜率分别为 k 1 ， k 2 . 如果 l 与 x 轴垂直，设 l ： x ＝ t ，由题设知 t ≠ 0 ，且 | t |<2 ， 从而可设 l ： y ＝ kx ＋ m ( m ≠ 1). 得 (4 k 2 ＋ 1) x 2 ＋ 8 kmx ＋ 4 m 2 － 4 ＝ 0 ， 由题设可知 Δ ＝ 16(4 k 2 － m 2 ＋ 1)>0. 由题设 k 1 ＋ k 2 ＝－ 1 ， 故 (2 k ＋ 1) x 1 x 2 ＋ ( m － 1)( x 1 ＋ x 2 ) ＝ 0. 当且仅当 m > － 1 时， Δ >0 ， 所以 l 过定点 (2 ，－ 1).