2018届二轮复习命题及其关系、充分条件与必要条件学案(全国通用)
1.2 命题及其关系、充分条件与必要条件
考情考向分析 命题的真假判断和充分、必要条件的判定是考查的主要形式,多与集合、函数、不等式、立体几何中的线面关系相交汇,考查 生的推理能力,题型为填空题,低档难度.
1.命题
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
2.四种命题及其相互关系
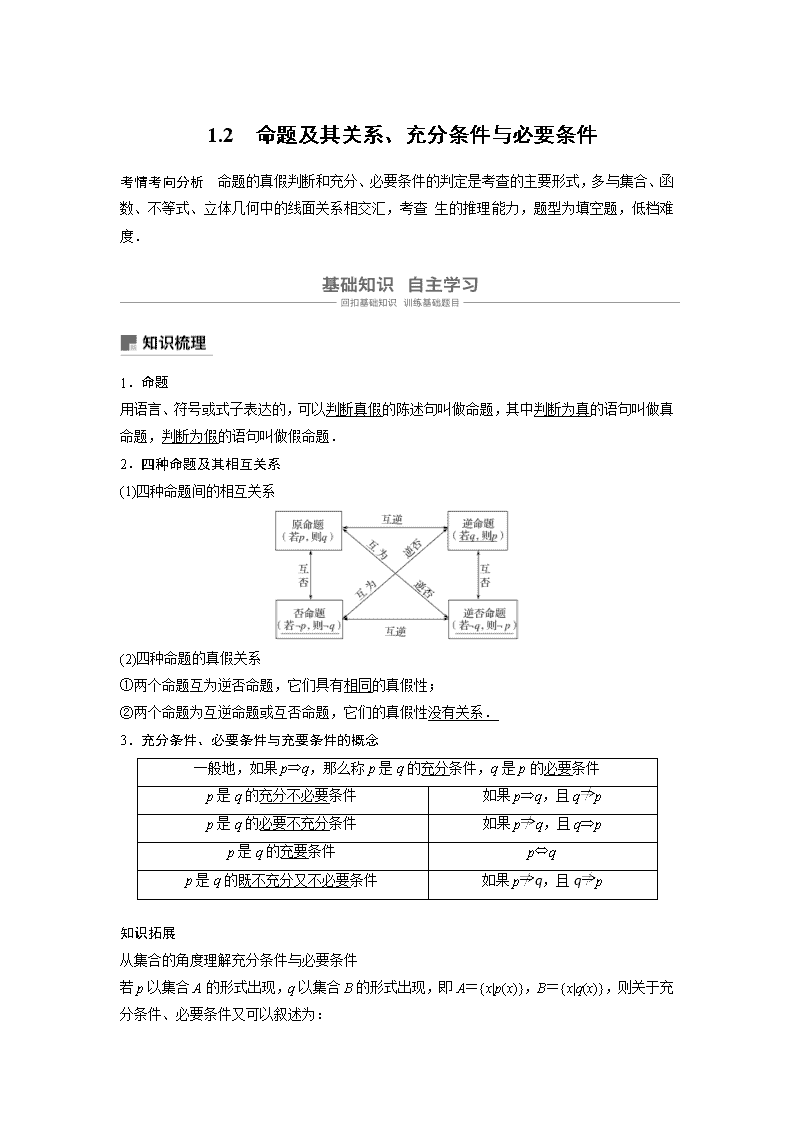
(1)四种命题间的相互关系
(2)四种命题的真假关系
①两个命题互为逆否命题,它们具有相同的真假性;
②两个命题为互逆命题或互否命题,它们的真假性没有关系.
3.充分条件、必要条件与充要条件的概念
一般地,如果p⇒q,那么称p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
如果p⇒q,且qp
p是q的必要不充分条件
如果pq,且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分又不必要条件
如果pq,且qp
知识拓展
从集合的角度理解充分条件与必要条件
若p以集合A的形式出现,q以集合B的形式出现,即A={x|p(x)},B={x|q(x)},则关于充分条件、必要条件又可以叙述为:
(1)若A⊆B,则p是q的充分条件;
(2)若A⊇B,则p是q的必要条件;
(3)若A=B,则p是q的充要条件;
(4)若AB,则p是q的充分不必要条件;
(5)若AB,则p是q的必要不充分条件;
(6)若A⃘B且A⊉B,则p是q的既不充分又不必要条件.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)“对顶角相等”是命题.( √ )
(2)命题“若p,则q”的否命题是“若p,则綈q”.( × )
(3)当q是p的必要条件时,p是q的充分条件.( √ )
(4)当p是q的充要条件时,也可说成q成立当且仅当p成立.( √ )
(5)若p是q的充分不必要条件,则綈p是綈q的必要不充分条件.( √ )
题组二 教材改编
2.[P8习题T2]下列命题是真命题的是________.(填序号)
①矩形的对角线相等;
②若a>b,c>d,则ac>bd;
③若整数a是素数,则a是奇数;
④命题“若x2>0,则x>1”的逆否命题.
答案 ①
3.[P7例1]“x-3=0”是“(x-3)(x-4)=0”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
题组三 易错自纠
4.命题“若x2>y2,则x>y”的逆否命题是________.
答案 若x≤y,则x2≤y2
解析 根据原命题和其逆否命题的条件和结论的关系,得命题“若x2>y2,则x>y”的逆否命题是“若x≤y,则x2≤y2”.
5.“sin α>0”是“α是第一象限角”的________条件.
答案 必要不充分
解析 由sin α>0,可得α是第一或第二象限角及终边在y轴正半轴上;若α
是第一象限角,则sin α>0,所以“sin α>0”是“α是第一象限角”的必要不充分条件.
6.已知集合A=,B={x|-1
3,即m>2.
题型一 命题及其关系
1.下列命题是真命题的是________.(填序号)
①若=,则x=y;
②若x2=1,则x=1;
③若x=y,则=;
④若x<y,则x2<y2.
答案 ①
2.某食品的广告词为“幸福的人们都拥有”,这句话的等价命题是________.
答案 不拥有的人们不幸福
3.下列命题:
①“若a21,则ax2-2ax+a+3>0的解集为R”的逆否命题;
④“若x(x≠0)为有理数,则x为无理数”的逆否命题.
其中正确的命题是________.
答案 ③④
解析 对于①,否命题为“若a2≥b2,则a≥b”,为假命题;对于②,逆命题为“面积相等的三角形是全等三角形”,为假命题;对于③,当a>1时,Δ=-12a<0,原命题正确,从而其逆否命题正确,故③正确;对于④,原命题正确,从而其逆否命题正确,故④正确.
4.设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是__________.
答案 若方程x2+x-m=0没有实根,则m≤0
思维升华 (1)写一个命题的其他三种命题时,需注意:
①对于不是“若p,则q”形式的命题,需先改写;
②若命题有大前提,写其他三种命题时需保留大前提.
(2)判断一个命题为真命题,要给出推理证明;判断一个命题是假命题,只需举出反例即可.
(3)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.
题型二 充分必要条件的判定
典例 (1)(2017·浙江改编)已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4+S6>2S5”的________条件.
答案 充要
解析 方法一 ∵数列{an}是公差为d的等差数列,
∴S4=4a1+6d,S5=5a1+10d,S6=6a1+15d,
∴S4+S6=10a1+21d,2S5=10a1+20d.
若d>0,则21d>20d,10a1+21d>10a1+20d,
即S4+S6>2S5.
若S4+S6>2S5,则10a1+21d>10a1+20d,
即21d>20d,
∴d>0.∴“d>0”是“S4+S6>2S5”的充要条件.
方法二 ∵S4+S6>2S5等价于S4+S4+a5+a6>2(S4+a5)等价于a6>a5等价于a5+d>a5等价于d>0,
∴“d>0”是“S4+S6>2S5”的充要条件.
(2)已知条件p:x>1或x<-3,条件q:5x-6>x2,则綈p是綈q的______条件.
答案 充分不必要
解析 由5x-6>x2,得2sin β不成立.
∴充分性不成立;
取α=,β=,sin α>sin β,但α<β,必要性不成立.
故“α>β”是“sin α>sin β”的既不充分又不必要条件.
(2)设向量a=(sin 2θ,cos θ),b=(cos θ,1),则“a∥b”是“tan θ=成立”的______________条件.(选填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 必要不充分
解析 a∥b等价于sin 2θ=cos2θ等价于cos θ=0或2sin θ=cos θ等价于cos θ=0或tan θ=,所以“a∥b”是“tan θ=成立”的必要不充分条件.
题型三 充分必要条件的应用
典例 已知P={x|x2-8x-20≤0},非空集合S={x|1-m≤x≤1+m}.若x∈P是x∈S的必要条件,求m的取值范围.
解 由x2-8x-20≤0,得-2≤x≤10,
∴P={x|-2≤x≤10}.
由x∈P是x∈S的必要条件,知S⊆P.
则
∴当0≤m≤3时,x∈P是x∈S的必要条件,即所求m的取值范围是[0,3].
引申探究
若本例条件不变,问是否存在实数m,使x∈P是x∈S的充要条件.
解 若x∈P是x∈S的充要条件,则P=S,
∴方程组无解,
即不存在实数m,使x∈P是x∈S的充要条件.
思维升华 充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:
(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
(2)要注意区间端点值的检验.
跟踪训练 (1)设p:|2x+1|0);q:>0.若p是q的充分不必要条件,则实数m的取值范围为__________.
答案 (0,2]
解析 由|2x+1|0),得-m<2x+10,得x<或x>1.
∵p是q的充分不必要条件,又m>0,
∴≤,∴01,∴命题p为假命题,
∴①不正确;
命题p的逆命题是“若a2<1,则a<1”,为真命题,
∴②正确;
命题p的否命题是“若a≥1,则a2≥1”,∴③不正确;
命题p的逆否命题是“若a2≥1,则a≥1”,∴④不正确.
5.“x>1”是“(x+2)<0”的________条件.
答案 充分不必要
解析 由x>1,得x+2>3,即(x+2)<0,(x+2)<0,得x+2>1,即x
>-1,故“x>1”是“(x+2)<0”成立的充分不必要条件.
6.若实数a,b满足a>0,b>0,则“a>b”是“a+ln a>b+ln b”的________条件.
答案 充要
解析 设f(x)=x+ln x,显然f(x)在(0,+∞)上单调递增,
∵a>b,∴f(a)>f(b),
∴a+ln a>b+ln b,故充分性成立;
∵a+ln a>b+ln b,
∴f(a)>f(b),∴a>b,故必要性成立,
故“a>b”是“a+ln a>b+ln b”的充要条件.
7.已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的________条件.
答案 充分不必要
解析 若直线a和直线b相交,则平面α和平面β相交;若平面α和平面β相交,那么直线a和直线b可能平行或异面或相交.
8.在△ABC中,角A,B均为锐角,则“cos A>sin B”是“△ABC为钝角三角形”的________条件.
答案 充要
解析 因为cos A>sin B,所以cos A>cos,
因为角A,B均为锐角,所以-B为锐角,
又因为余弦函数y=cos x在(0,π)上单调递减,
所以A<-B,所以A+B<,
在△ABC中,A+B+C=π,所以C>,
所以△ABC为钝角三角形;
若△ABC为钝角三角形,角A,B均为锐角,
则C>,所以A+B<,
所以A<-B,所以cos A>cos,
即cos A>sin B.
故“cos A>sin B”是“△ABC为钝角三角形”的充要条件.
9.“若a≤b,则ac2≤bc2”,则原命题及命题的逆命题、否命题和逆否命题中真命题的个数是________.
答案 2
解析 其中原命题和逆否命题为真命题,逆命题和否命题为假命题.
10.设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的________条件.(选填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
解析 当x>1,y>1时,x+y>2一定成立,即p⇒q,
当x+y>2时,可令x=-1,y=4,即q⇏p,
故p是q的充分不必要条件.
11.已知命题p:a≤x≤a+1,命题q:x2-4x<0,若p是q的充分不必要条件,则a的取值范围是________.
答案 (0,3)
解析 令M={x|a≤x≤a+1},N={x|x2-4x<0}={x|0<x<4}.
∵p是q的充分不必要条件,∴MN,
∴解得0<a<3.
12.有下列几个命题:
①“若a>b,则a2>b2”的否命题;②“若x+y=0,则x,y互为相反数”的逆命题;③“若x2<4,则-2<x<2”的逆否命题.
其中真命题的序号是________.
答案 ②③
解析 ①原命题的否命题为“若a≤b,则a2≤b2”,错误;
②原命题的逆命题为“若x,y互为相反数,则x+y=0”,正确;
③原命题的逆否命题为“若x≥2或x≤-2,则x2≥4”,正确.
13.已知p:函数f(x)=|x+a|在(-∞,-1)上是单调函数,q:函数g(x)=loga(x+1)(a>0,且a≠1)在(-1,+∞)上是增函数,则綈p是q的________条件.
答案 充要
解析 易知p成立等价于a≤1,q成立等价于a>1,所以綈p成立等价于a>1,则綈p是q的充要条件.
14.已知条件p:2x2-3x+1≤0,条件q:x2-(2a+1)x+a(a+1)≤0.若綈p是綈q的必要不充分条件,则实数a的取值范围是________.
答案
解析 方法一 命题p为,
命题q为{x|a≤x≤a+1}.
綈p对应的集合A=,
綈q对应的集合B={x|x>a+1或x0,即2n+1>2λ对任意的n∈N*都成立,于是可得3>2λ,即λ<.
故所求λ的取值范围是.
16.设a,b为正数,则“a-b>1”是“a2-b2>1”的________条件.(选填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
解析 ∵a-b>1,即a>b+1.又∵a,b为正数,
∴a2>(b+1)2=b2+1+2b>b2+1,即a2-b2>1成立;反之,当a=,b=1时,满足a2-b2>1,但a-b>1不成立.所以“a-b>1”是“a2-b2>1”的充分不必要条件.