2019届二轮复习选择填空题解题策略焦点弦问题学案（全国通用）

2019届二轮复习选择填空题解题策略焦点弦问题学案（全国通用）

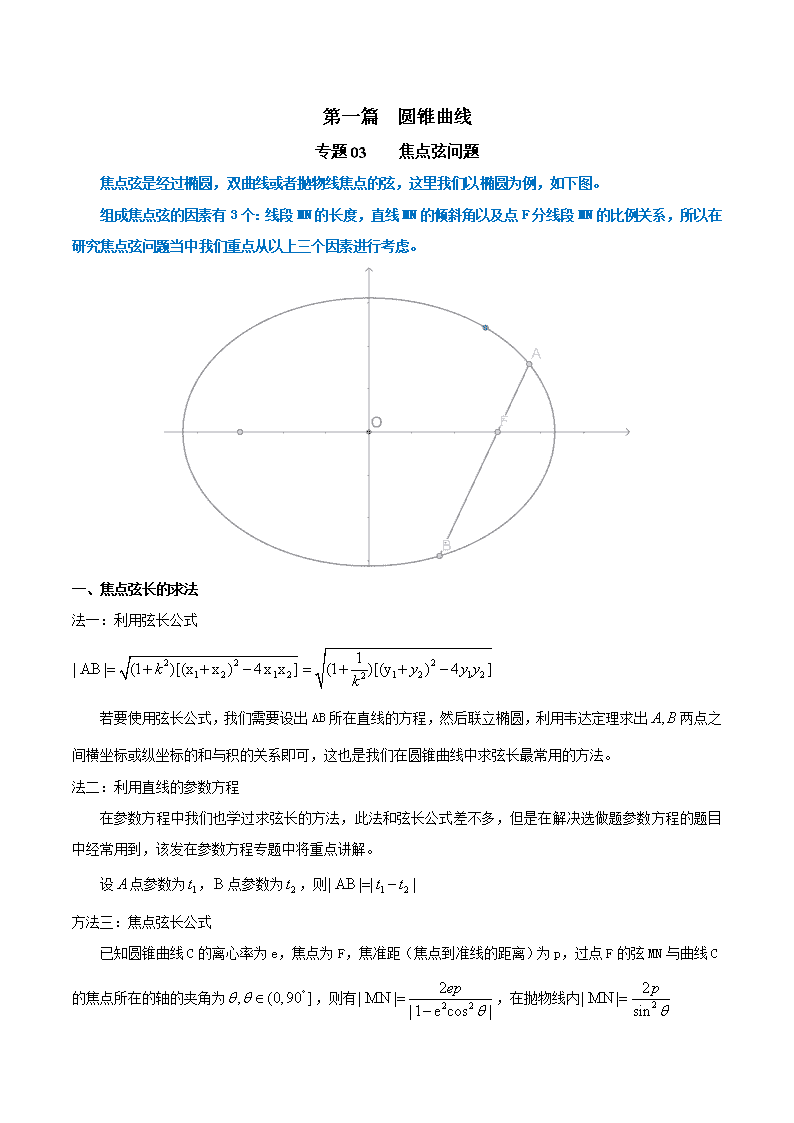
第一篇 圆锥曲线 专题03 焦点弦问题 焦点弦是经过椭圆，双曲线或者抛物线焦点的弦，这里我们以椭圆为例，如下图。‎ 组成焦点弦的因素有3个：线段MN的长度，直线MN的倾斜角以及点F分线段MN的比例关系，所以在研究焦点弦问题当中我们重点从以上三个因素进行考虑。‎ 一、焦点弦长的求法 法一：利用弦长公式 若要使用弦长公式，我们需要设出AB所在直线的方程，然后联立椭圆，利用韦达定理求出两点之间横坐标或纵坐标的和与积的关系即可，这也是我们在圆锥曲线中求弦长最常用的方法。‎ 法二：利用直线的参数方程 在参数方程中我们也学过求弦长的方法，此法和弦长公式差不多，但是在解决选做题参数方程的题目中经常用到，该发在参数方程专题中将重点讲解。‎ 设点参数为，点参数为，则 方法三：焦点弦长公式 已知圆锥曲线C的离心率为e，焦点为F，焦准距（焦点到准线的距离）为p，过点F的弦MN与曲线C的焦点所在的轴的夹角为，则有，在抛物线内 证明过程如下：‎ 设，根据第二定义可知 在中，，代入上式得：‎ ‎，解得 同理可得 例1：已知椭圆的右焦点为F，经过F且倾斜角为的直线与椭圆相交于不同的两点，已知.‎ ‎（1）求离心率；‎ ‎（2）若，求椭圆方程.‎ ‎【解析】（1）求离心率套公式即可 ‎，代入求得 套用公式解得 又因为，故可解出 椭圆方程为 例2：已知F为抛物线的焦点，过F作两条互相垂直的直线，直线与C交于两点，直线与C交于两点，则的最小值为________.‎ 例3：过抛物线的焦点F，且斜率为的直线交C于点M（M在x轴上方），l为C的准线，点N在l上且，则M到直线的距离为_________.‎ 二、在焦点弦中三要素之间的关系 上面求得焦点弦长公式与离心率有关，因此下面我们探究一下求离心率，倾斜角以及点分线段的比例之间的关系。学 ‎ 设为大于1的数，因此选取的都是长比短的数值，设为弦长与焦点所在的对称轴的夹角（锐角），根据上面求出的的长度，代入整理即可得出三者之间的关系式：（此公式适用于椭圆，双曲线中内分弦，抛物线），在双曲线中，如果焦点F外分弦时，‎ 注意：在双曲线中内分弦是直线与双曲线的一支有两个交点；外分弦是直线与双曲线的两支各有一个交点，判断是内分弦还是外分弦只需要看这条直线的斜率和渐近线的斜率的大小即可。‎ 例4：已知双曲线的右焦点为F，过F且斜率为的直线交于两点（全都在右支上），若 ‎，求双曲线的离心率。‎ ‎【解析】题目是内分弦的形式，用公式. ‎ 其中 解得 例5：已知双曲线的离心率为，过左焦点F且斜率为的直线交双曲线的两支于 学 ‎ 两点，若，求 的值.‎ ‎【解析】题目是外分弦的形式，用公式，，‎ ‎ 代入可得 ‎ 这里需要注意的值，永远都有共同的一点F，且 例6：过抛物线的焦点F作倾斜角为的直线，与抛物线交于两点（点A在y轴左侧），则=___________.‎ ‎【解析】题目中，如果套公式很容易错以为，记住是直线与对称轴的正方向所成的 锐角，故，从题目中知，设，则套公式可知，所 学 ‎ 以 ‎ 三、双曲线中与焦点弦问题相关的交点个数问题 双曲线由于两支独立，因此双曲线上过焦点的直线与双曲线交点的个数有待确定，如果过右支上焦点的直线与右支交于两点，则这两点即为焦点弦，但是何时过右支的焦点的直线与右支只和右支有一个焦点呢？ 学 ‎ 上图中，判断过焦点弦与双曲线交点的位置关系问题，只需要判断焦点弦所在直线的斜率和双曲线渐近线的斜率即可，若，则焦点弦所在的直线与双曲线只有一个交点，若，则直线与双曲线有两个交点且左右各有一个，若，则直线与双曲线有两个交点且都在同一支上。‎ 例7：已知双曲线的右焦点为F，若过F且倾斜角为的直线与双曲线的右支有且只有一个交点，则此双曲线的离心率的取值范围是___________.‎ ‎ ‎