安徽省安庆市桐城市某中学2020届高三高考模拟考试数学（理）试卷

安徽省安庆市桐城市某中学2020届高三高考模拟考试数学（理）试卷

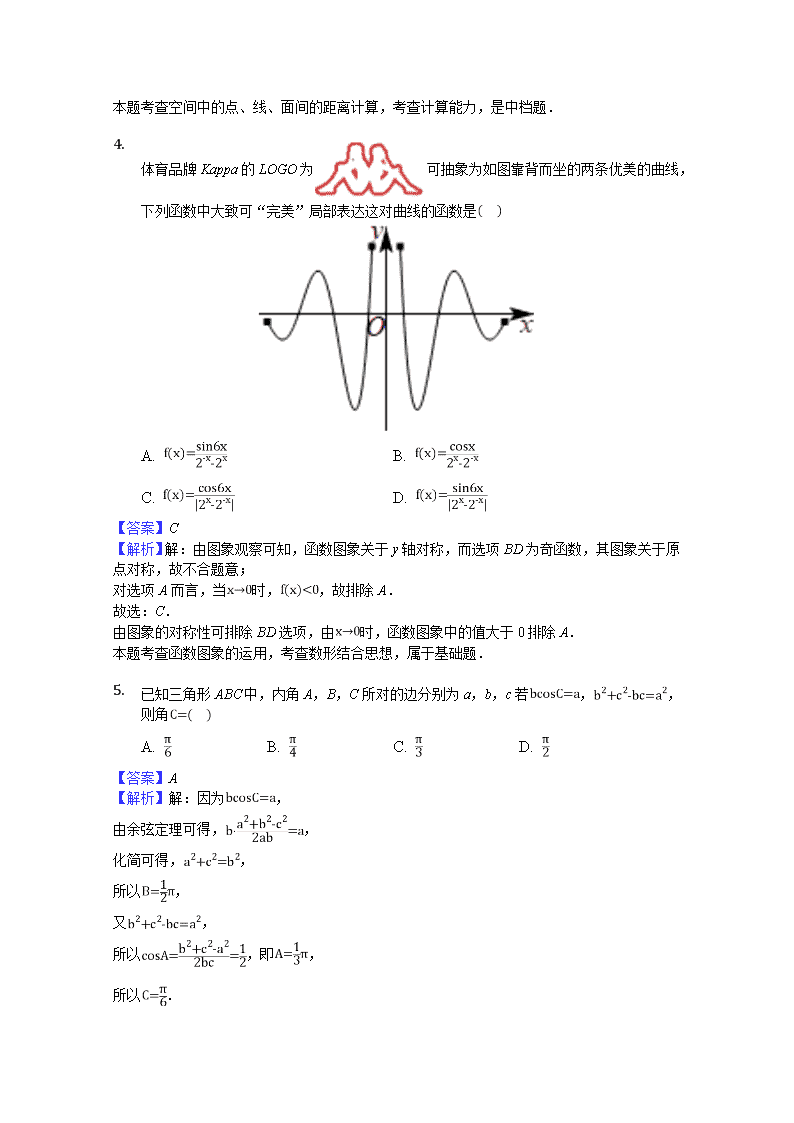
数学试卷 一、选择题（本大题共12小题，共60.0分）‎ 1. 己知全集，，，则 A. B. C. D. ‎ ‎【答案】A ‎【解析】解：全集，，， 则， 则， 故选：A． 求出，再计算出结果． 考本题查集合的交并补运算，基础题． ‎ 2. 设为虚数单位，其中x，y是实数，则等于 A. 5 B. C. D. 2‎ ‎【答案】A ‎【解析】解：为虚数单位，其中x，y是实数， ，，解得：，． 则． 故选：A． 利用复数相等、模的计算公式即可得出． 本题考查了复数相等、模的计算公式，考查了推理能力与计算能力，属于基础题． ‎ 3. 埃及金字塔是古埃及的帝王法老陵墓，世界七大奇迹之一，其中较为著名的是胡夫金字塔．令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿，还有发生在胡夫金字塔上的数字“巧合”如胡夫金字塔的底部周长如果除以其高度的两倍，得到的商为，这就是圆周率较为精确的近似值．金字塔底部形为正方形，整个塔形为正四棱锥，经古代能工巧匠建设完成后，底座边长大约230米．因年久风化，顶端剥落10米，则胡夫金字塔现高大约为 A.  米 B.  米 C.  米 D.  米 ‎【答案】C ‎【解析】解：设金字塔风化前的形状如图， ，其底面周长为， 由题意可得：， ． 胡夫金字塔现高大约为米． 结合选项可得，胡夫金字塔现高大约为米． 故选：C． 由已知求出底面周长，再由底部周长除以高度的两倍等于求得高，减去10‎ 得答案． 本题考查空间中的点、线、面间的距离计算，考查计算能力，是中档题． ‎ 1. 体育品牌Kappa的LOGO为可抽象为如图靠背而坐的两条优美的曲线，下列函数中大致可“完美”局部表达这对曲线的函数是 A. B. C. D. ‎ ‎【答案】C ‎【解析】解：由图象观察可知，函数图象关于y轴对称，而选项BD为奇函数，其图象关于原点对称，故不合题意； 对选项A而言，当时，，故排除A． 故选：C． 由图象的对称性可排除BD选项，由时，函数图象中的值大于0排除A． 本题考查函数图象的运用，考查数形结合思想，属于基础题． ‎ 2. 已知三角形ABC中，内角A，B，C所对的边分别为a，b，c若，，则角 A. B. C. D. ‎ ‎【答案】A ‎【解析】解：因为， 由余弦定理可得，， 化简可得，， 所以， 又， 所以，即， 所以 ‎． 故选：A． 由已知结合余弦定理进行化简可求B，A，进而可求C． 本题主要考查了余弦定理在求解三角形中的应用，属于基础试题． ‎ 1. 若A，B分别是直线与x轴，y轴的交点，圆C：上有任意一点M，则的面积的最大值是 A. 6 B. ‎8 ‎C. 10 D. 12‎ ‎【答案】C ‎【解析】解：如图， 圆C：上的点M到直线AB距离的最大值为， ，，则． 则的面积的最大值是． 故选：C． 由题意画出图形，利用点到直线的距离公式求出M到直线AB距离的最大值，则的面积的最大值可求． 本题考查直线与圆位置关系的应用，考查数形结合的解题思想方法，是中档题． ‎ 2. 在中，点F为线段BC上任一点不含端点，若，则的最小值为 A. 1 B. ‎8 ‎C. 2 D. 4‎ ‎【答案】B ‎【解析】解：由于点F在线段BC上，由向量共线定理可得， 则， 故选：B． 由向量共线定理可得，然后利用1的代换，结合基本不等式即可求解． 本题主要考查了向量共线定理的应用，还考查了利用基本不等式求解最值中的1的代换技巧的应用． ‎ 3. 我省5名医学专家驰援湖北武汉抗击新冠肺炎疫情现把专家全部分配到A，B，C三个集中医疗点，每个医疗点至少要分配1人，其中甲专家不去A医疗点，则不同分配种数为 A. 116 B. ‎100 ‎C. 124 D. 90‎ ‎【答案】B ‎【解析】解：根据题意，分2步进行分析： ，将5名医学专家分为3组， 若分为2、2、1的三组，有种分组方法， 若分为3、1、1的三组，有种分组方法， 则有种分组方法； ，将分好的三组分派到三个医疗点，甲专家所在组不去A医疗点，有2种情况，再将剩下的2组分派到其余2个医疗点，有2种情况， 则3个组的分派方法有种情况， 则有种分配方法； 故选：B． 根据题意，分2步进行分析：，将5名医学专家分为3组，，将分好的三组分派到三个医疗点，由分步计数原理计算可得答案． 本题考查排列、组合的应用，涉及分步计数原理的应用，属于基础题． ‎ 1. 将函数的图象向左平移个单位，所得图象对应的函数在区间上无极值点，则m的最大值为 A. B. C. D. ‎ ‎【答案】A ‎【解析】解：将函数的图象向左平移个单位，可得的图象， 根据所得图象对应的函数在区间上无极值点，，且， 求得，则m的最大值为， 故选：A． 由题意利用函数的图象变换规律，正弦函数的图象的单调性，求得m的最大值． 本题主要考查函数的图象变换规律，正弦函数的图象的单调性，属于基础题． ‎ 2. 过双曲线的左焦点引圆的切线，切点为T，延长交双曲线右支于P点，M为线段的中点，O为坐标原点，则 A. 1 B. C. D. 2‎ ‎【答案】B ‎【解析】解：由图象可得 ‎ ‎， 故选：B． 画出图形，利用双曲线的定义转化求解即可． 本题考查双曲线的简单性质的应用，考查转化思想以及计算能力，是中档题． ‎ 1. 已知三棱锥的四个顶点在球O的球面上，球O的半径为4，是边长为6的等边三角形，记的外心为若三棱锥的体积为则 A. B. C. D. ‎ ‎【答案】D ‎【解析】解：由题意可得：，，． 设点P到平面BAC的高为h，由，解得． 点P所在小圆与所在平面平行上运动，． ． ． 故选：D． 由题意可得：，，设点P到平面BAC的高为h，由，解得可得点P所在小圆与所在平面平行上运动，即可得出． 本题考查了球的性质、勾股定理、等边三角形的面积计算公式、三棱锥的体积计算公式，考查了推理能力与计算能力，属于基础题． ‎ 2. 已知函数，的最小值为3，若存在，，使得，则正整数n的最大值为 A. 2 B. ‎3 ‎C. 4 D. 5‎ ‎【答案】B ‎【解析】解：求导，， 当或时，在恒成立， 从而在单调递减，， 解得，不合题意， 当时，易得在单调递减，在单调递增， ，解得不合题意， 当时，在单调递增，所以，满足题意， 所以， 所以，，所以，， 依题意有，即，得，又因为 ‎， 所以，所以n的最大值为3， 故选：B． 求导，根据函数单调性，最值与函数单调性的关系，即可求得a的值，求得的最大值为根据题意，，根据，即可求得n的最大值． 本题考查利用导数判断函数的单调性及最值，考查参数的取值范围，考查分类讨论思想，属于难题． ‎ 二、填空题（本大题共4小题，共20.0分）‎ 1. 已知向量，，两向量的夹角为，则______．‎ ‎【答案】‎ ‎【解析】解：因为向量，，两向量的夹角为； ． 故答案为： 直接根据向量夹角的计算公式把已知条件代入即可求解 本题考查向量的夹角，考查向量的模长以及计算，考查计算能力． ‎ 2. 的展开式中的系数为__________用数字填写答案．‎ ‎【答案】40‎ ‎【解析】【分析】 本题考查了二项式定理及分类讨论思想，属中档题． 由二项式定理及分类讨论思想得：的展开式的通项为，则的展开式中的系数为，得解． 【解答】 解：由的展开式的通项为， 则的展开式中的系数为， 故答案为40． ‎ 3. 某市一次高三年级数学统测，经抽样分析，成绩X近似服从正态分布，且该市某校有400人参加此次统测，估计该校数学成绩不低于90分的人数为______‎ ‎【答案】80‎ ‎【解析】解：成绩X近似服从正态分布，且， ， 成绩不低于90分的人数为． 故答案为80． 本题利用正态分布的对称性得到，从而得到成绩不低于90分的人数． 本题考查了正态分布的性质：对称性的应用．难度较低，属于基础题． ‎ 1. 设抛物线的焦点为F，过点的直线与抛物线相交于A，B两点，与抛物线的准线相交于C，，则和的面积之比为______．‎ ‎【答案】‎ ‎【解析】解：抛物线方程为，焦点F的坐标为， 准线方程为， 如图，设，， 过A，B分别向抛物线的准线作垂线，垂足分别为E，N， 则， ， 把代入抛物线，得，， 直线AB过点与 方程为，代入抛物线方程，解得， ， 在中，， ：：：， 和的面积之比为：： 故答案为： 利用三角形面积公式，可把与的面积之比转化为BC长与AC长的比，再根据抛物线的焦半径公式转化为A，B到准线的距离之比，借助求出B点坐标，得到AB方程，代入抛物线方程，解出A点坐标，就可求出BN与AE的长度之比，得到所需问题的解． 本题主要考查了抛物线的焦半径公式，侧重了学生的转化能力，以及计算能力 ‎ 三、解答题（本大题共7小题，共82.0分）‎ 2. 某医院体检中心为回馈大众，推出优惠活动：对首次参加体检的人员，按200元次收费，并注册成为会员，对会员的后续体检给予相应优惠，标准如下：‎ 体检次序 第一次 第二次 第三次 第四次 第五次及以上 收费比例 ‎1‎ 该休检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计，得到数据如表：‎ 检次数 一次 两次 三次 四次 五次及以上 频数 ‎60‎ ‎20‎ ‎12‎ ‎4‎ ‎4‎ 假设该体检中心为顾客体检一次的成本费用为150元，根据所给数据，解答下列问题：Ⅰ已知某顾客在此体检中心参加了3次体检，求这3次体检，该体检中心的平均利润；Ⅱ该体检中心要从这100人里至少体检3次的会员中，按体检次数用分层抽样的方法抽出5人，再从这5人中抽取2人，每人发放现金200元．用5表示体检3次的会员所得现金和，求的分布列及．‎ ‎【答案】解：医院3次体检的收入为， 三次体验的成本为， 故平均利润为元； 根据题意抽取的5个人中3人体检三次，1人体检四次，1人体验5次及以上， ，200，400， ， ． ， 分布列如下：‎ ‎ 0‎ ‎ 200‎ ‎ 400‎ ‎ P ‎ ‎ ‎ ‎ ‎．‎ ‎【解析】根据题意求出即可； 利用分层抽样求出5个人中3人体检三次，1人体检四次，1人体验5次及以上，，200，400，求出分布列和期望即可． 考查离散型随机变量求分布列和数学期望，中档题． ‎ 1. 已知数列为等差数列，，且，，依次成等比数列． 求数列的通项公式； 设，数列的前n项和为，若，求n的值．‎ ‎【答案】解：设数列为公差为d的等差数列， ，即，即， ，，依次成等比数列，可得 ，即， 解得， 则； ， 即有前n项和为 ‎ ‎， 由，可得， 解得．‎ ‎【解析】设等差数列的公差为d，运用等差数列的通项公式和等比数列中项性质，解方程可得首项和公差，即可得到所求通项公式； 求得，运用裂项相消求和可得，解方程可得n． 本题考查等差数列的通项公式和等比数列的中项性质，考查数列的裂项相消求和，以及方程思想和运算能力，属于基础题． ‎ 1. 如图，已知多面体PABCDE的底面ABCD是边长为2的菱形，平面ABCD，，且． 证明：平面平面PCE； 若直线PC与平面ABCD所成的角为，求平面CPB与平面CDE所成锐二面角的余弦值． ‎ ‎【答案】解：证明：连结BD，交AC于点O，取PC中点F，连结OF、EF， 多面体PABCDE的底面ABCD是边长为2的菱形，平面ABCD， ，，O是AC中点， ，平面PAC， 是PC中点，平面ABCD，，且． ，四边形EFOD是平行四边形，， 平面PAC， 平面PCE，平面平面PCE． 解：平面ABCD，，平面ABCD， 以O为原点，OB为x轴，OC为y轴，OF为z轴，建立空间直角坐标系， 直线PC与平面ABCD所成的角为，底面ABCD是边长为2的菱形，， ， ，0，，1，，0，，0，， 1，，2，，1，，0，， 设平面CPB的法向量y，， 则，取，得1，， 设平面CDE的法向量b，‎ ‎， 则，取，得， 设平面CPB与平面CDE所成锐二面角为， 则． 平面CPB与平面CDE所成锐二面角的余弦值为．‎ ‎【解析】连结BD，交AC于点O，取PC中点F，连结OF、EF，推导出，，从而平面PAC，推导出，四边形EFOD是平行四边形，，从而平面PAC，由此能证明平面平面PCE． 由平面ABCD，，得平面ABCD，以O为原点，OB为x轴，OC为y轴，OF为z轴，建立空间直角坐标系，利用向量法能求出平面CPB与平面CDE所成锐二面角的余弦值． 本题考查面面垂直的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题． ‎ 1. 已知直线l：，椭圆C；，，分别为椭圆的左右焦点．Ⅰ当直线l过右焦点时，求C的标准方程；Ⅱ设直线l与椭圆C交于A，B两点，O为坐标原点，且，，若点O在以线段GH为直径的圆内，求实数a的取值范围．‎ ‎【答案】解：Ⅰ直线l：经过右焦点， ，解得， 又，， 椭圆C的标准方程为：；Ⅱ设，， 联立方程，消去x得：， ，解得， 且有，， 由，，可求得，， ， 设M是GH的中点，则， 点O在以线段GH为直径的圆内， ‎ ‎， 即，整理得：， ， ，即， 又，且， ， 实数a的取值范围为：．‎ ‎【解析】Ⅰ把右焦点的坐标代入直线l的方程求得a的值，即可得到C的标准方程；Ⅱ设，，联立直线l与椭圆方程，根据求出a的范围，且利用韦达定理表示出和，根据，可知，，表达出，设M是GH的中点，则表示出M的坐标，进而根据，整理可得：，把和的表达式代入求得m的取值范围，最后综合可得答案． 本题主要考查了椭圆方程，直线与椭圆的位置关系，以及点与圆的位置关系，是中档题． ‎ 1. 已知函数Ⅰ当时，求的单调增区间；Ⅱ若，且在上有唯一的零点，求证：‎ ‎【答案】解：Ⅰ当时，，， ， 即，解得， 的单调递增区间为；Ⅱ， ， 令，解得，， 当时，，单调递减， 当，，，单调递增， ，， 在上有唯一的零点， ，且， ，， ，， 消去a可得 ‎， 设，， 恒成立， 在上单调递减， ，， ．‎ ‎【解析】Ⅰ先求导，根据导数和函数单调性的关系即可求出；Ⅱ先求导，可得函数的单调区间，在上有唯一的零点，可得，且，根据，，消a可得，再设，，利用导数和函数零点存在定理即可求出． 本题考查了导数和函数的函数单调性的关系，函数零点存在定理，属于中档题． ‎ 1. 在平面直角坐标系xOy中，曲线C：以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，直线l的极坐标方程为． 求曲线C的极坐标方程和直线l的普通方程； 设直线与直线l交于点M，与曲线C交于P，Q两点，求的值．‎ ‎【答案】解：将C的方程化为， 故其极坐标方程为， l的普通方程是． 将代入C的极坐标方程得， 故， 将代入l的极坐标方程得，即， 所以．‎ ‎【解析】直接利用转换关系式的应用，把参数方程极坐标方程和直角坐标方程之间进行转换． 利用极径的应用求出结果． 本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，极径的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型． ‎ 2. 已知函数． 当时，解不等式； 若，，求证：．‎ ‎【答案】解：当时，，可化为， 此时． 当时，，可得不等式无解； 当时，，即，则； 当时，恒成立， 综上，不等式的解集为． 证明：由，，得，， 则， 故．‎ ‎【解析】将原不等式化为，由绝对值的意义去绝对值符号，解不等式求并集可得所求解集； 由题意可得，，两式相加，结合绝对值不等式的性质，以及不等式的传递性，即可得证． 本题考查绝对值不等式的解法，注意运用分类讨论思想，考查不等式的证明，注意运用绝对值不等式的性质和不等式的性质，考查运算能力和推理能力，属于中档题． ‎