山西省运城市2019-2020学年高二上学期期末调研测试 数学（理）

山西省运城市2019-2020学年高二上学期期末调研测试 数学（理）

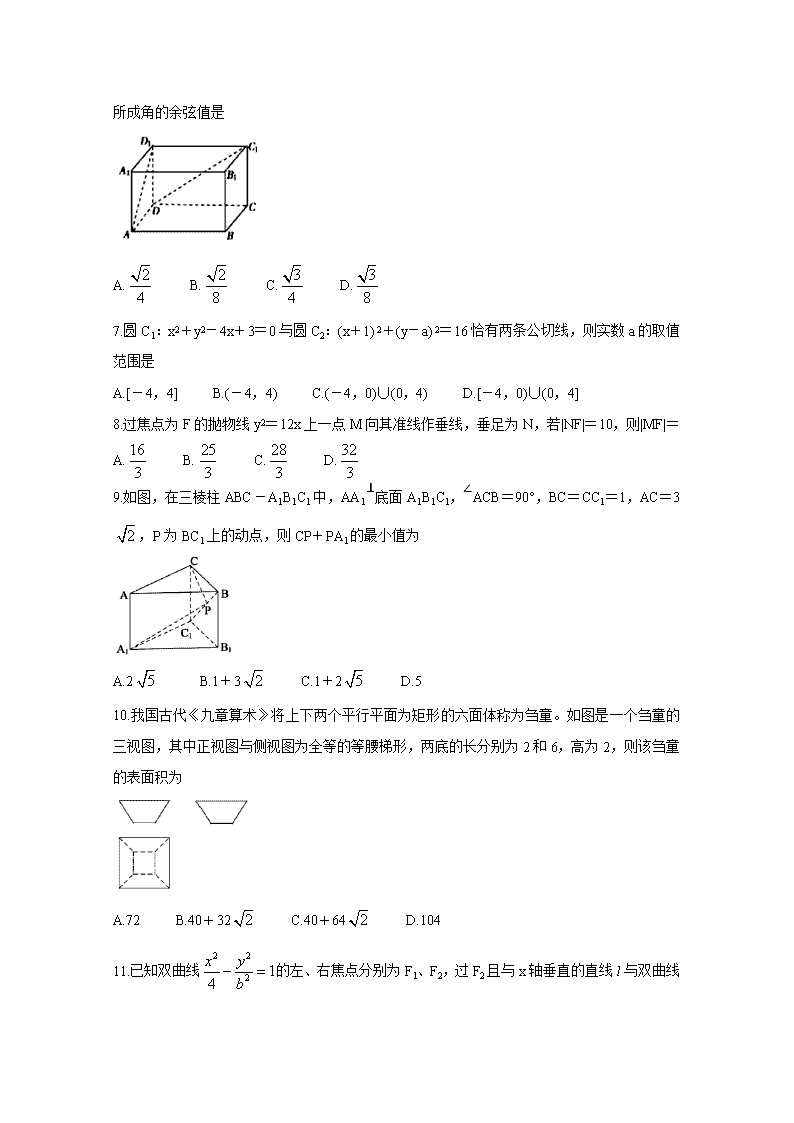
运城市2019－2020学年度第一学期期末调研测试 高二数学(理)试题 ‎2020.1‎ 本试题满分150分，考试时间120分钟。答案一律写在答题卡上。‎ 注意事项：‎ ‎1.答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。‎ ‎2.答题时使用0.5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎3.请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。‎ ‎4.保持卡面清洁，不折叠，不破损。‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.曲线的焦距是 A.6 B.10 C.8 D.2 ‎ ‎2.设直线l1的方向向量＝(1，2，－2)，直线l2的方向向量＝(－2，3，m)，若l1⊥l2，则实数m的值为 A.1 B.2 C. D.3‎ ‎3.命题“在△ABC中，若sinA＝，则A≠30°”的否命题是 A.在△ABC中，若sinA＝，则A≠30° B.在△ABC中，若sinA≠，则A＝30°‎ C.在△ABC中，若sinA≠，则A≠30° D.在△ABC中，若A≠30°，则sinA≠‎ ‎4.已知命题p：“a＝1”是“直线l1：ax＋2y－4＝0与l2：x＋(a＋1)y＋2＝0平行”的充要条件；命题q：对任意x∈R，总有2x>0。则下列命题为真命题的是 A.(p)∨(q) B.p∧(q) C.p∧q D.(p)∧q ‎5.已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题中正确的是 A.若α//β，mα，nβ，则m//n B.若α//β，m⊥β，则m⊥α C.若α⊥β，mα，nβ，则m⊥n D.若α⊥β，m⊥β，则m//α ‎6.如图，长方体ABCD－A1B1C1D1中，∠DAD＝45°，∠CDC1＝30°，那么异面直线AD1与DC1‎ 所成角的余弦值是 A. B. C. D.‎ ‎7.圆C1：x2＋y2－4x＋3＝0与圆C2：(x＋1) 2＋(y－a) 2＝16恰有两条公切线，则实数a的取值范围是 A.[－4，4] B.(－4，4) C.(－4，0)∪(0，4) D.[－4，0)∪(0，4]‎ ‎8.过焦点为F的抛物线y2＝12x上一点M向其准线作垂线，垂足为N，若|NF|＝10，则|MF|＝‎ A. B. C. D.‎ ‎9.如图，在三棱柱ABC－A1B1C1中，AA1⊥底面A1B1C1，∠ACB＝90°，BC＝CC1＝1，AC＝3，P为BC1上的动点，则CP＋PA1的最小值为 A.2 B.1＋3 C.1＋2 D.5‎ ‎10.我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童。如图是一个刍童的三视图，其中正视图与侧视图为全等的等腰梯形，两底的长分别为2和6，高为2，则该刍童的表面积为 A.72 B.40＋32 C.40＋64 D.104‎ ‎11.已知双曲线的左、右焦点分别为F1、F2，过F2且与x轴垂直的直线l 与双曲线的两条渐近线分别交于A、B两点，|AB|＝3，M(4，1)，若双曲线上存在一点P使得|PM|＋|PF2|≤t，则t的最小值为 A.5 B. C.5＋4 D.5－4‎ ‎12.在棱长为1的正四面体A－BCD中，E是BD上一点，，过E作该四面体的外接球的截面，则所得截面面积的最小值为 A. B. C. D.‎ 二、填空题 ‎13.无论m取何值，直线x＋my－4m－1＝0恒过定点 。‎ ‎14.在平行六面体ABCD－A1B1C1D1中，各棱长都等于2，且∠BAA1＝∠DAA1＝∠BAD＝60°，则AC1的长为 。‎ ‎15.已知抛物线C：y2＝6x，直线l过点P(2，2)，且与抛物线C交于M，N两点，若线段MIN的中点恰好为点P，则直线l的斜率为 。‎ ‎16.已知椭圆的左右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且|PT|的最小值不小于(a－c)，则椭圆的离心率的取值范围是 。‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。‎ ‎17.(本小题10分)‎ 已知p：x2－8x－20≤0；q：x2－2mx－3m2≤0(m>0)，且ρ是q的充分不必要条件，求实数m的取值范围。‎ ‎18.(本小题12分)‎ 已知线段AB的端点B的坐标是(2，0)，端点A在圆(x＋2)2＋y2＝16上运动，M是线段AB的中点。‎ ‎(1)求动点M的轨迹方程。‎ ‎(2)已知点C(－2，－2)，D(－2，6)，E(4，－2)，求|MC|2＋|MD|2＋|ME|2的最大值和最小值。‎ ‎19.(本小题12分)‎ 如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB//CD，AB＝AD＝2，CD＝4，M为CE的中点。‎ ‎(1)求证：BM//平面ADEF；‎ ‎(2)求证：平面BDE⊥平面BEC。‎ ‎20.(本小题12分)‎ 已知平面上动点P到定点F(2，0)的距离比P到直线x＝－1的距离大1。记动点P的轨迹为曲线C。‎ ‎(1)求曲线C的方程；‎ ‎(2)过点(－2，0)的直线l交曲线C于A、B两点，点A关于x轴的对称点是D，证明：直线BD恒过点F。‎ ‎21.(本小题12分)‎ 如图，在四面体A－BCD中，AD⊥平面BCD，BC⊥CD。AD＝2，BD＝2。M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ＝3QC。‎ ‎(1)证明：PQ⊥AD；‎ ‎(2)若二面角C－BM－D的大小为60°，求∠BDC的大小。‎ ‎22.(本小题12分)‎ 已知椭圆，A(2，0)是长轴的一个端点，弦BC过椭圆的中心O，点C在第一象限，且＝0，。‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设P、Q为椭圆上不重合的两点且异于A、B，若∠PCQ的平分线总是垂直于x轴，问是否存在实数λ，使得 ?若不存在，请说明理由；若存在，求λ的最大值。‎