- 2021-06-30 发布 |
- 37.5 KB |
- 16页

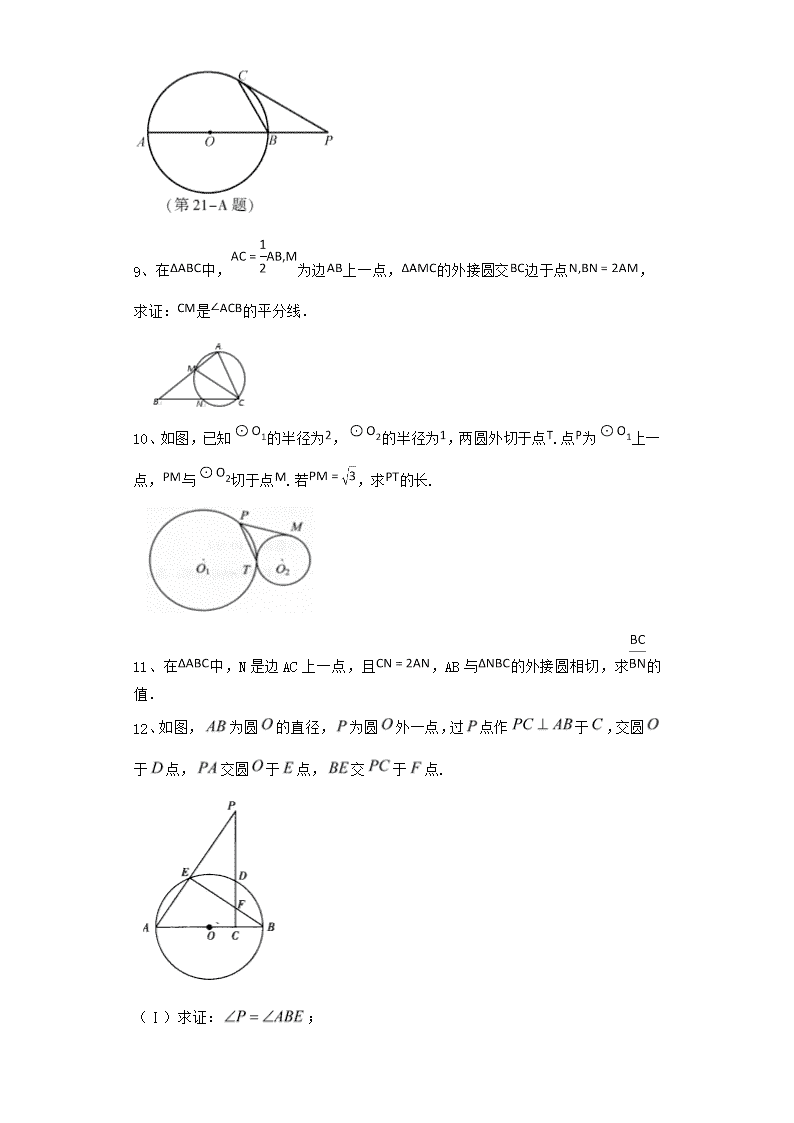

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版 直线与圆的位置关系 课时作业
2020届一轮复习人教A版 直线与圆的位置关系 课时作业 1、已知为圆上的三点,若,圆的半径为,则( ) A. B. C. D. 2、如图,在中, . 是的外心, 于, 于, 于,则 等于( ) A. B. C. D. 3、我国古代数学名著《九章算术》在“勾股”一章中有如下数学问题:“今有勾八步,股十五步,勾中容圆,问径几何?”.意思是一个直角三角形的两条直角边的长度分别是8步和15步,则其内切圆的直径是多少步?则此问题的答案是( ) A. 3步 B. 6步 C. 4步 D. 8步 4、已知圆的半径为1, 为该圆的两条切线, 为两切点,那么的最小值为 A. B. C. D. 5、设D是半径为R的圆周上的一定点,在圆周上随机取一点C,连接CD得一弦,若A表示“所得弦的长大于圆内接等边三角形的边长”,则P(A)=_____. 6、设D是半径为R的圆周上的一定点,在圆周上随机取一点C,连接CD得一弦,若A表示“所得弦的长大于圆内接等边三角形的边长”,则P(A)=_____. 7、在四边形中,,,为等边三角形,则的外接圆与的内切圆的公共弦长=__________. 8、如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若,求BC的长. 9、在中,为边上一点,的外接圆交边于点, 求证:是的平分线. 10、如图,已知的半径为,的半径为,两圆外切于点.点为上一点,与切于点.若,求的长. 11、在中,N是边AC上一点,且,AB与的外接圆相切,求的值. 12、如图,为圆的直径,为圆外一点,过点作于,交圆于点,交圆于点,交于点. (Ⅰ)求证:; (Ⅱ)求证: 13、如图,圆的半径垂直于直径,为上一点,的延长线交圆于点,过点的切线交的延长线于点,连接. (1)求证:; (2)若,,求的长. 14、如图,A,B,C是⊙O上的3个不同的点,半径OA交弦BC于点D.求证:. 15、如图,是圆的直径,弦的延长线相交于点垂直的延长线于点.求证: 16、如图,四边形是圆的内接四边形,的延长线与的延长线交于点,且. (1)证明:; (2)设不是圆的直径,的中点为,且,证明:为等边三角形. 17、如图,切于点,直线交于两点,,垂足为. (1)证明: (2)若,,求圆的直径. 18、如图,在中,是的角平分线,的外接圆交于点,. (Ⅰ)求证:; (Ⅱ)当时,求的长. 19、如图,为圆的直径,在圆上,于,点为线段上任意一点,延长交圆于,. (1)求证:; (2)若,求的值. 20、选修4-1:几何证明选讲 如图,是的切线,过圆心, 为的直径,与相交于、两点,连结、. (1) 求证:; (2) 求证:. 参考答案 1、答案:D 分析:画出图形,根据向量关系得四边形为菱形,可将问题转化为求的值. 详解:如下图所示,由, 知四边形是边长为的菱形, 且,. 名师点评:本题主要是根据题设中给出的向量关系,利用将问题转化为求解的值,再根据向量的数量积公式得出结论. 2、答案:B 如图,连接, ,同理可得,设的半径为,则; ; ,故,故选B. 3、答案:B 由于该直角三角形的两直角边长分别是和,则得其斜边长为, 设其内切圆半径为,则有 (等积法), 解得,故其直径为 (步),故选B. 4、答案:A 如图所示:设,则 所以当且仅当时取“=”,故最小值为 考点:向量的数量积的应用 5、答案: 如图,△DPQ为圆内接正三角形,当点C位于劣弧PQ上时,弦DC>PD,所以P(A)= . 6、答案: 如图,△DPQ为圆内接正三角形,当点C位于劣弧PQ上时,弦DC>PD,所以P(A)=. 7、答案:1 如图所示建立平面直角坐标系,为等边的中心. 则的外接圆为:,的内切圆半径为:. 由得.两圆的公共弦为EF, 则. 故答案为:1. 8、答案:2 试题分析:分析:先连圆心与切点得直角三角形,求出PO,即得B为中点,再根据直角三角形斜边上中线长等于斜边一半的性质得结果. 详解:证明:连结OC.因为PC与圆O相切,所以OC⊥PC. 又因为PC=,OC=2, 所以OP==4. 又因为OB=2,从而B为Rt△OCP斜边的中点,所以BC=2. 名师点评:本题考查圆与三角形等基础知识,考查推理论证能力. 9、答案:试题分析:分析:先证明△MBN∽△CBA,再证明AM=MN,最后证明CM是∠ACB的平分线. 详解:证明:连结MN,则∠BMN=∠BCA, 又∠MBN=∠CBA,因此△MBN∽△CBA. 所以.又因为AC=AB,所以=2,即BN=2MN. 又因为BN=2AM,所以AM=MN, 所以CM是∠ACB的平分线. 名师点评:本题主要考查几何证明选讲等基础知识,意在考查学生对这些基础知识的掌握能力及分析推理能力. 10、答案: 试题分析: 作辅助线,即延长交与点,连结,,,则过点.则得,然后证得,根据相似三角形的性质可得,从而可求得. 试题 延长交与点,连结,,,则过点. 由切割线定理得:. 因为,与均为等腰三角形, 所以, 所以, 所以,即. 又, 所以. 11、答案:. 试题分析:记外接圆为,利用圆的切割线定理和相似三角形进行求解. 试题记外接圆为,、分别是圆的切线和割线,所以, 又,所以与相似,所以,所以 ,. 12、答案:(1)见解析;(Ⅱ)见解析. 试题分析:(1)在中,;在中, ;即可证明 (Ⅱ)由题意的,列出比例关系式,即可证明 试题 (1),所以在中,;在中, ;所以 (Ⅱ)在中,,由①得, ,所以 13、答案:(1)证明见解析;(2)1. 试题分析: (1)连接ON,由题意结合弦切角定理即可证得题中的结论; (2)解法一:由题意结合相交弦定理可求得外接圆半径,则. 解法二:由题意结合正弦定理求得外接圆半径,则. 解法三:由题意得到关于圆的半径的方程,解方程可得半径,则. 试题 (1)证明:连接, ∵为的切线,∴90°, 在中,∵, ∴,又∵, ∴, 根据弦切角定理,得,∴. (2)解法一:∵, ∴为等边三角形,∴. 设的半径为, 则在直角三角形中,,,, 根据相交弦定理,, 可得, 即可得,, ∴. 解法二:∵60°, ∴△PMN为等边三角形,∴, 设的半径为r,则在直角三角形中,,,, 又为的外接圆, 由正弦定理可知,, 又, ∴,∴. 解法三:, 设的半径为r,则在直角三角形中,,,, 在中,,∴, 又∵,MN=PM=1, ∴,∴,∴. 14、答案:试题分析:延长交⊙O于点E,则,根据,即可得证. 试题证明:延长交⊙O于点E,则. ∵, ∴. ∴. 15、答案:试题分析:四点共圆,所以,又△∽△,所以,即,得证。 试题 A.连接,因为为圆的直径,所以, 又,则四点共圆, 所以. 又△∽△, 所以,即, ∴. 16、答案:试题分析:(1)利用四边形是的内接四边形,可得,由,可得,即可证明:; (2)设的中点为,连接,证明,可得,进行可得,即可证明为等边三角形. 试题 (1)由题设知A,B,C,D四点共圆,所以, 由已知得,故. (2)设BC的中点为N,连结MN,则由知, 故O在直线MN上. 又AD不是圆O的直径,M为AD的中点,故, 即. 所以,故, 又,故. 由(1)知,,所以为等边三角形. 17、答案:(1)见解析;(2)3 试题分析:(1)根据直径的性质,即可证明; (2)结合圆的切割线定理进行求解,即可求出的直径. 试题 (1)因为是的直径, 则 又,所以 又切于点, 得 所以 (2)由(1)知平分, 则, 又,从而, 所以 所以, 由切割线定理得 即, 故, 即的直径为3. 18、答案:(I)证明见解析;(II). 试题分析:(I)连接DE,证明∽,利用AB=AC,结合角平分线性质,即可证明;(II)根据割线定理得,从而可求AD的长. 试题(Ⅰ)连接, 因为是圆内接四边形,所以 又∽,即有 又因为,可得 因为是的平分线,所以,从而 (Ⅱ)由条件知,设,则, 根据割线定理得,即 即,解得或(舍去),则 【考点】与圆有关的性质的应用. 19、答案:(1)见解析,(2)4 试题分析:(1)连接,∵,∴,又,∴为等边三角形,∵,∴为中边上的中线,∴;(2)连接,证明,∴,即. 试题 (1)证明: 连接, ∵,∴, 又, ∴为等边三角形, ∵, ∴为中边上的中线, ∴;. (2)解:连接, ∵,边等边三角形, 可求得, ∵为圆的直径,∴, ∴, 又∵,∴, ∴, 即 【考点】几何证明选讲. 20、答案:试题分析:本小题主要考查平面几何的证明及其运算,具体涉及到共圆图形的判断和圆的性质以及两个三角形全等的判断和应用等有关知识内容.本小题针对考生的平面几何思想与数形结合思想作出考查.(1)利用弦切角进行转化证明;(2)借助三角形相似和切割线定理进行证明. 试题(1) 由是圆的切线,因此弦切角的大小等于夹弧所对的圆周角,在等腰中,,可得,所以. (5分) (2) 由与相似可知,,由切割线定理可知,,则,又,可得. (10分) 考点:平面几何的证明及其运算 查看更多