2019届二轮复习（文）小题标准练（六）作业（全国通用）

2019届二轮复习（文）小题标准练（六）作业（全国通用）

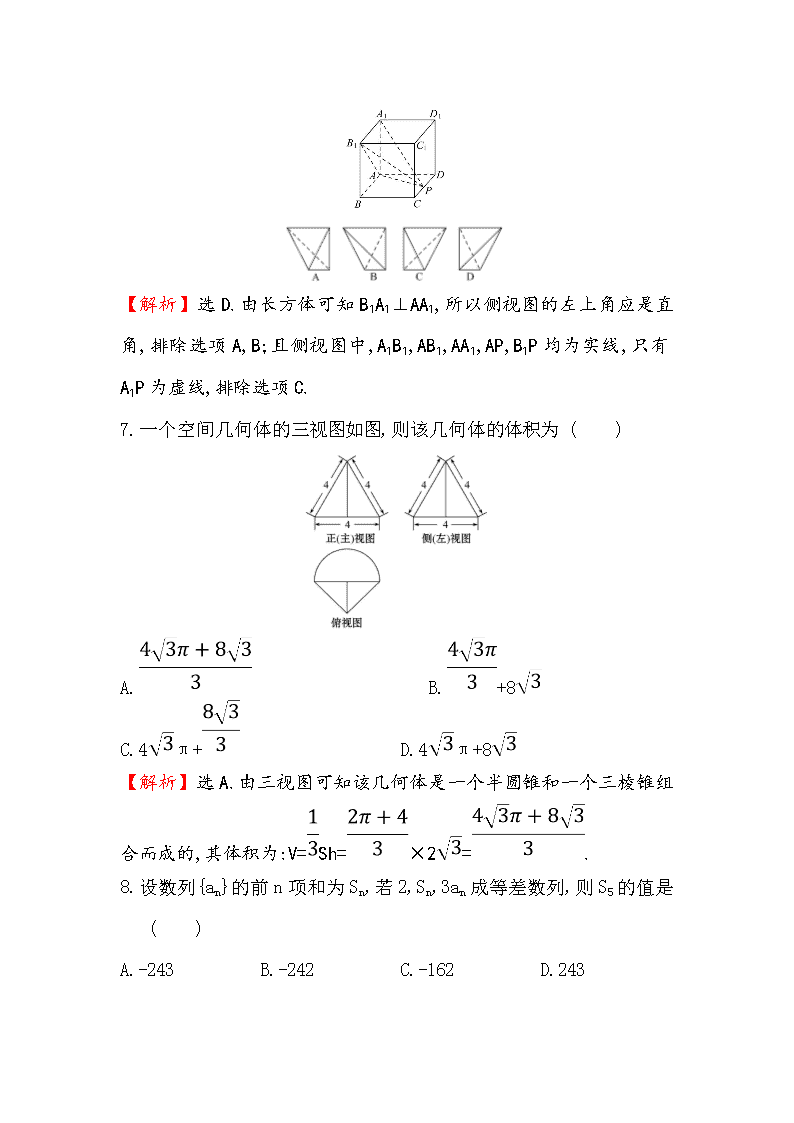
小题标准练(六)‎ ‎(40分钟　80分)‎ 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)　　　　　　　　　　　　　　　　　　　‎ ‎1.若复数满足i(z-1)=1+i(i为虚数单位),则z= (　　)‎ A.2-i B.2+i C.1-2i D.1+2i ‎【解析】选A.由已知得iz=1+2i,所以z==2-i.‎ ‎2.若复数z满足z(4-i)=5+3i(i为虚数单位),则为 (　　)‎ A.1-i　 B.-1+i C.1+i　 D.-1-i ‎【解析】选A.z====1+i,=1-i.‎ ‎3.下列函数中,既是偶函数又在(-∞,0)上单调递增的是 (　　)‎ A.y=x2　 B.y=2|x|‎ C.y=log2 D.y=sin x ‎【解析】选C.函数y=x2在(-∞,0)上是减函数;函数y=2|x|在(-∞,0)上是减函数;函数y=log2=-log2|x|是偶函数,且在(-∞,0)上是增函数;函数y=sin x不是偶函数.综上所述,选C.‎ ‎4.在△ABC中,“cos A=2sin Bsin C”是“△ABC为钝角三角形”的 (　　)‎ A.必要不充分条件 B.充要条件 C.充分不必要条件 D.既不充分也不必要条件 ‎【解析】选C.在△ABC中,A=π-(B+C),所以cos A=-cos(B+C).又因为 cos A=2sin Bsin C,‎ 即-cos Bcos C+sin Bsin C=2sin Bsin C.所以cos(B-C)=0,所以B-C=,所以 B为钝角.即△ABC为钝角三角形.若△ABC为钝角三角形,当A为钝角时,条件不成立.‎ ‎5.函数f(x)=x2-bx+c满足f(x+1)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是 (　　)‎ A.f(bx)≤f(cx) B.f(bx)≥f(cx)‎ C.f(bx)>f(cx) D.与x有关,不确定 ‎【解析】选A.由f(x+1)=f(1-x)知:函数f(x)的图象关于直线x=1对称,所以b=2,由f(0)=3知c=3,所以f(bx)=f(2x),f(cx)=f(3x).当x>0时,3x>2x>1,又函数f(x)在[1,+∞)上单调递增,所以f(3x)>f(2x),即f(bx)f(2x),即f(bx)==.‎ ‎10.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.‎ 该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为 (　　)‎ A.2 017×22 015 B.2 017×2 2 014‎ C.2 016×22 015 D.2 016×22 014‎ ‎【解析】选B.‎ 如图,当第一行3个数时,最后一行仅一个数,为8=23-2×(3+1);‎ 当第一行4个数时,最后一行仅一个数,为20=24-2×(4+1);‎ 当第一行5个数时,最后一行仅一个数,为48=25-2×(5+1);‎ 当第一行6个数时,最后一行仅一个数,为112=26-2×(6+1).‎ 归纳推理,得当第一行2 016个数时,最后一行仅一个数,为22 016-2×(2 016+1).‎ ‎11.设O为坐标原点,P是以F为焦点的抛物线y2=2px(p>0) 上任意一点,M是线段PF上的点,且=2|MF|,则直线OM的斜率的最大值为 ‎ (　　)‎ A. B.　 C. D.1‎ ‎【解析】选C.设P(2pt2,2pt),M(x,y)(不妨设t>0),则=(2pt2-,2pt).由已知得=,‎ 所以 所以 ‎ 所以kO M==≤=,‎ 所以(kO M)max=.‎ ‎12.若x,y满足且z=y-x的最小值为-4,则k的值为 (　　)‎ A.2 B.-2 C.　 D.-‎ ‎【解析】选D.作出线性约束条件的可行域.当k>0时,如图①所示,此时可行域为y轴上方、直线x+y-2=0的右上方、直线kx-y+2=0的右下方的区域,显然此时z=y-x无最小值.‎ 当k<-1时,z=y-x取得最小值2;当k=-1时,z=y-x取得最小值-2,均不符合题意.‎ 当-1y>0的实数x,y恒成立,则实数c的最大值为____________. ‎ ‎【解析】因为不等式2y2-x2≥c(x2-xy)对任意满足x>y>0的实数x,y恒成立,所以c≤=,令=t>1,所以c≤,令f(t)=,则f′(t)= =,‎ 当t>2+时,f′(t)>0,函数f(t)单调递增;当1

查看更多