高中数学：《平行线分线段成比例定理》课件4（新人教A版选修4-1）

高中数学：《平行线分线段成比例定理》课件4（新人教A版选修4-1）

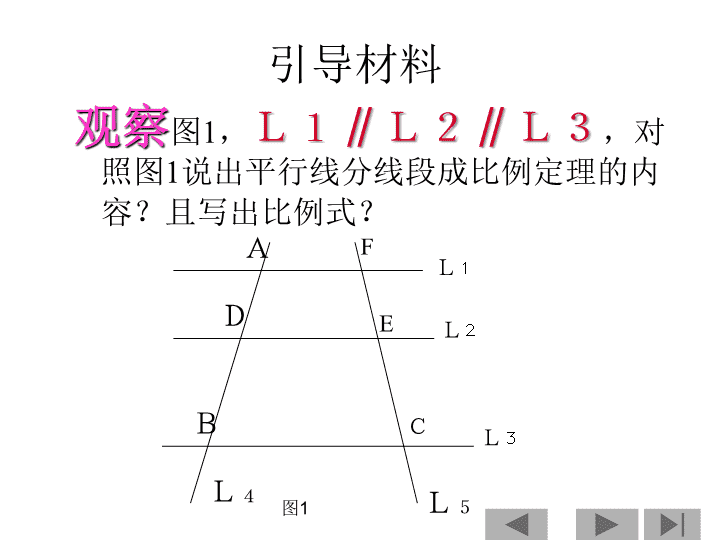
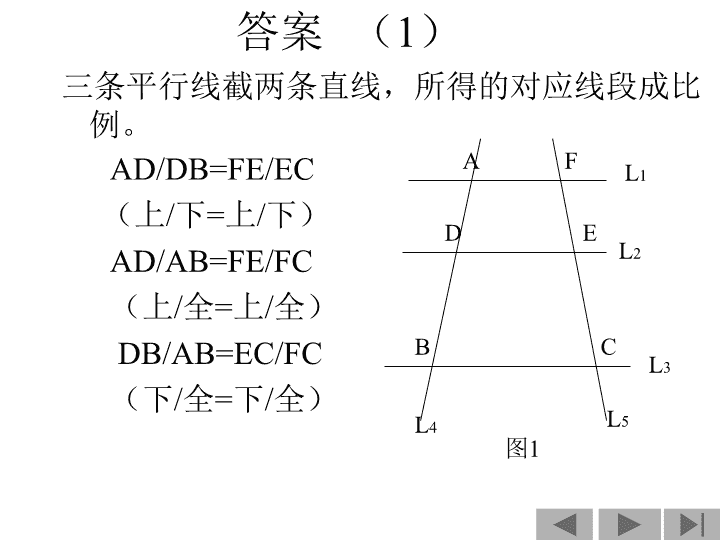
平行线分线段成比例定理（ 2 ） 学习目标 ： 1 、 会 识别平行线分线段成比例的变式图形。 2 、 能 写出图中的成比例线段。 3 、 理解 平行线分线段成比例定理的推论。 4 、 会 用推论去计算和证明有关的问题。 5 、 建立 一种解题模型。 6 、 会 用 “ 运动 ” 的观点去研究解决问题。 7 、 欣赏 数学的美学文化 —— 理性美、结构美。 引导材料 观察 图 1 ， Ｌ１∥Ｌ２∥Ｌ３ ，对照 图 1 说 出平行线分线段成比例定理的内容？且写出比例式？ 图 1 Ａ Ｄ Ｂ F E Ｃ Ｌ １ Ｌ ２ Ｌ ３ Ｌ ５ Ｌ ４ 答案 （ 1 ） 三条平行线截两条直线，所得的对应线段成比例。 AD/DB=FE/EC （上 / 下 = 上 / 下） AD/AB=FE/FC （上 / 全 = 上 / 全） DB/AB=EC/FC （下 / 全 = 下 / 全） A D B F E C L 1 L 2 L 3 L 4 L 5 图 1 答案（ 2 ） DB/AD=EC/FE （下 / 上 = 下 / 上） AB/AD=FC/FE ( 全 / 上 = 全 / 上 ) AB/DB=FC/EC ( 全 / 下 = 全 / 下 ) A D B F E C L 1 L 2 L 3 L 4 L 5 图 1 教学设计（ 1 ） 1 . 观察 图 2 、图 3 ，说出它们分别是由图 1 怎样变化得到的？且写出图 2 、图 3 中有关的比例式？ A D B F E C A D B E C L 1 L 2 L 3 L 1 L 2 L 3 图 1 图 2 （ ） 怎样变化？ 一般到 特殊 平行移动直线 FC 与直线 AB 相交，交点 A 在 L 1 上。 (F) 教学设计（ 1 ）续 续观察 A D B F E C L 1 L 2 L 3 图 1 （ ） F A D B C L 1 L 2 L 3 图 3 怎样变化？ 一般到特殊 平行移动直线 FC 与直线 AB 相交 , 交点 D 在 L 2 上 (E) 教学设计（ 2 ） 思考： 把图 2 、图 3 中的部分线擦去，得到图 4 、图 5 ，上述比例式还成立吗？ A D B E L 1 L 2 L 3 C 部分线擦去 , 取一部分 A D B E C （ ） 字母 型 A 比例式 ， 因为 图 2 图 4 一般到特殊 成立 图形中有关的对应线段均没改变 教学设计（ 2 ）续 续思考 F A D B C （ E ） 图 3 部分线擦去 , 取一部分 F A D （ E ） B C 图 5 （字母 型） 比例式 ， 因为 一般到特殊 成立 图形中有关的对应线段均没改变 X 教学设计（ 3 ） 猜想： ⑴在图 4 、图 5 中，原题的条件（三条平行线）发生了什么变化？⑵结论有没有变？⑶ 猜一猜，你能发现什么规律 ？ A D B E C A D B E C 图 2 图 4 F A D B C （ E ） F A D （ E ） B C 图 3 图 5 部分线擦去 , 取一部分 一般到特殊 部分线擦去 , 取一部分 一般到特殊 （ 1 ）三条平行线剩下两条，且变为三角形的一边和截三角形另两边或两边延长线的线段。其中图 4 中 DE∥BC ，图 5 中 AF∥BC （ 2 ）结论没变，所得的对应线段成比例。 （ 3 ）推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例。 例题解析 已知： DE∥BC ， AB ＝ 15 ， BD ＝ 4 ， AC ＝ 9 ， 求： AE 的长？ 证明：∵ DE∥BC ∴AB/BD=AC/CE （ 平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例。） 即 15/4=9/CE ∴CE=12/5 ∴AE=AC+CE =9+12/5 =11.4 A B D C E 图 6 课堂练习（ 1 ）及答案 已知： DE∥BC ， AB ＝ 14 ， AC ＝ 18 ， AE ＝ 10 求： AD 的长？ 解：∵ DE∥BC ∴AD/AB=AE/AC （ 平行于三角形一边的直线截其他两边，所得的对应线段成比例。） 即 AD/14=10/18 ∴AD=70/9 A D B E C 图 7 课堂练习（ 2 ）及答案 已知： ED∥BC ， AB ＝ 5 ， AC ＝ 7 ， AD ＝ 2 求： AE 的长？ 解：∵ ED∥BC ∴ AD/AB=AE/AC （ 平行于三角形一边的直线截其它两边的延长 线，所得的对应线段成比例） 即 2/5=AE/7 ∴AE=14/5 E D A B C 图 8 5 7 2 课堂练习（ 3 ）及答案 已知： AB⊥BD ， ED⊥BD ，垂足分别为 B 、 D 求证： AC ／ EC ＝ BC ／ DC 证明：∵ AB⊥BD ， ED⊥BD ∴∠B=∠D=90° ∴AB∥DE ∴AC/EC=BC/DC （ 平行于三角形一边的直线截其它两边的延长线， 所得的对应线段成比例） A B C D E ┓ └ 图 9 知识目标小结 1. 定理名称 : 2. 文字语言 : 3. 图形语言 : 4. 符号语言 : 5. 模型语言 : A D E B C F A D B C 字母 型 字母 型 图 4 图 5 平行线分线段成比例定理的推论或三角形一边平行线的性质定理 平行于三角形一边的直线截其它两边（或两边的延长线），所得的对应线段成比例。 若 DE∥BC 若 AF∥BC 则： 则： A X 能力目标小结 1 、 平行线分线段成比例定理是研究相似形最重要、最基本的理论基础，而字母 A 型、 字母 X 型又是解决相似三角形一章有关计算和证明的模具，可构造或寻找字母 A 型、字母 X 型解决问题，把它称为三角形相似问题“奠基法” 。 2 、学会用“动态”的观点去解决研究问题。 3 、欣赏模型 “ 字母 A 型、字母 X 型 ” 的理性美、结构美，诱发学习数学的激情，感受数学的美学文化，培养学生 “ 自主实践、自主探索、大胆猜想、归纳创新 ” 的数学理念。 补充练习 1. 已知 : 点 E 在平行四边形 ABCD 的边 AB 的延长线上， DE 分别交 AC 、 BC 于点 F 、 G ，在图中找出字母 A 型图、字母 X 型图。 A B E D C G F 图 10 答案（ 3 ） 字母 A 型图 字母 X 型图 A B C D E F G A B C D E F G A B D C E F G 图 10-1 图 10-3 图 10-4 图 10-2 A D B C F G E 作业 1 、如图：∠ A=∠C ， AB/BC=3/2 ， BE=8 。求 BD= ？ 2 、已知： FG∥AE∥BC ， GH∥CD ，求： AF/BF=EH/HD A D E C B A B C E D F G H 再见 再见 再见