高三数学二轮高考专题辅导与训练打包检测试题：专题四第1讲课时训练提能

高三数学二轮高考专题辅导与训练打包检测试题：专题四第1讲课时训练提能

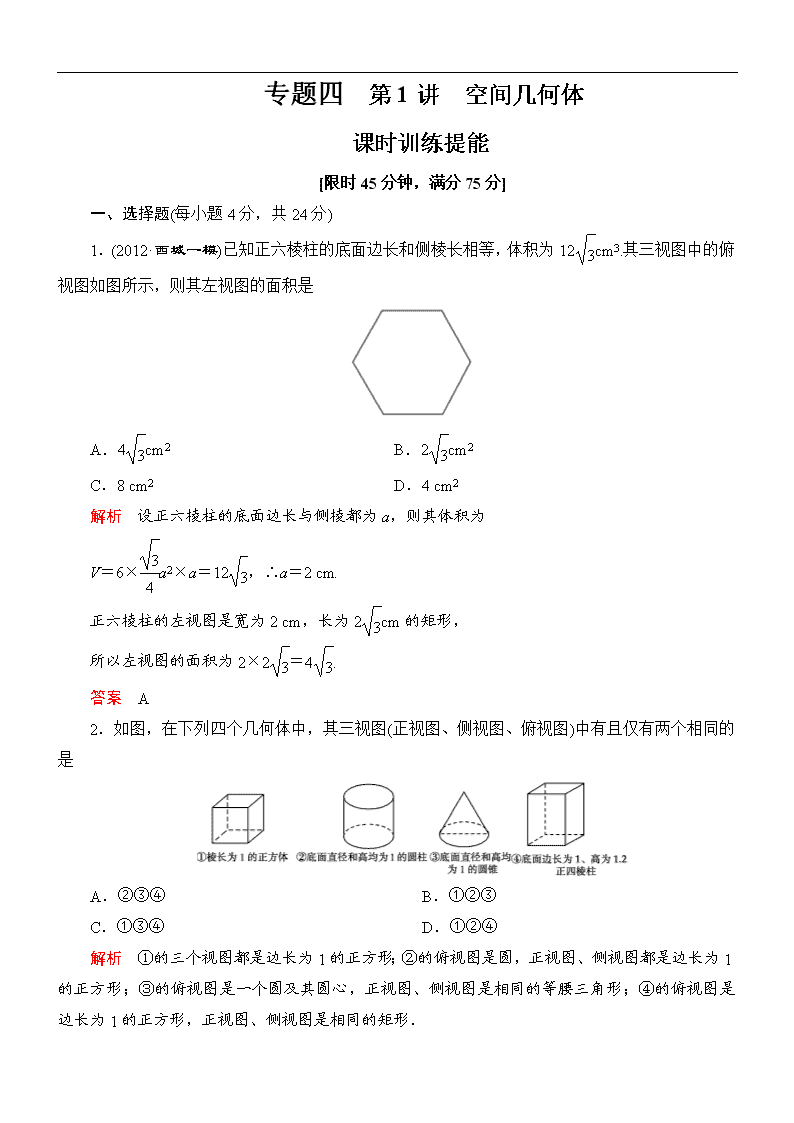
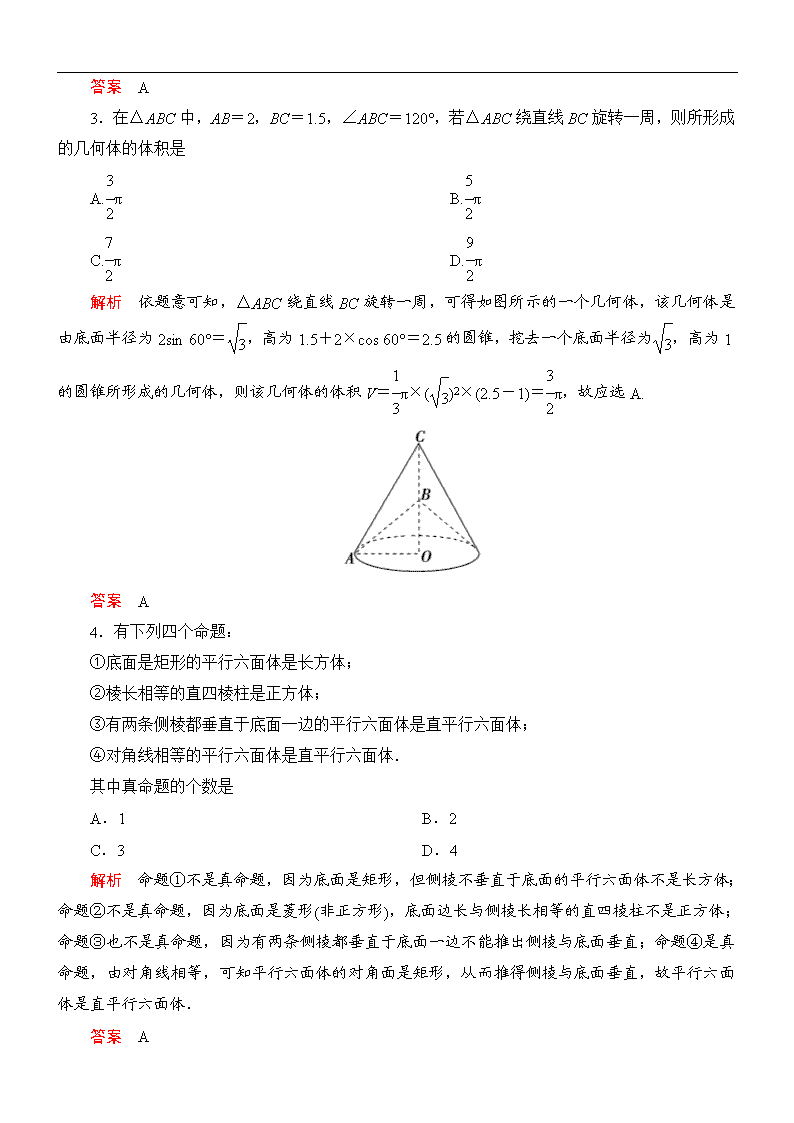
专题四 第1讲　空间几何体 课时训练提能 ‎[限时45分钟，满分75分]‎ 一、选择题(每小题4分，共24分)‎ ‎1．(2012·西城一模)已知正六棱柱的底面边长和侧棱长相等，体积为‎12cm3.其三视图中的俯视图如图所示，则其左视图的面积是 A．‎4cm2　　 B．‎2cm2‎ C．‎8 cm2　　 D．‎4 cm2‎ 解析　设正六棱柱的底面边长与侧棱都为a，则其体积为 V＝6×a2×a＝12，∴a＝‎2 cm.‎ 正六棱柱的左视图是宽为2 cm，长为2cm的矩形，‎ 所以左视图的面积为2×2＝4.‎ 答案　A ‎2．如图，在下列四个几何体中，其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是 A．②③④ B．①②③‎ C．①③④ D．①②④‎ 解析　①的三个视图都是边长为1的正方形；②的俯视图是圆，正视图、侧视图都是边长为1的正方形；③的俯视图是一个圆及其圆心，正视图、侧视图是相同的等腰三角形；④的俯视图是边长为1的正方形，正视图、侧视图是相同的矩形．‎ 答案　A ‎3．在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°，若△ABC绕直线BC 旋转一周，则所形成的几何体的体积是 A.π B.π C.π D.π 解析　依题意可知，△ABC绕直线BC旋转一周，可得如图所示的一个几何体，该几何体是由底面半径为2sin 60°＝，高为1.5＋2×cos 60°＝2.5的圆锥，挖去一个底面半径为，高为1的圆锥所形成的几何体，则该几何体的体积V＝π×()2×(2.5－1)＝π，故应选A.‎ 答案　A ‎4．有下列四个命题：‎ ‎①底面是矩形的平行六面体是长方体；‎ ‎②棱长相等的直四棱柱是正方体；‎ ‎③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；‎ ‎④对角线相等的平行六面体是直平行六面体．‎ 其中真命题的个数是 A．1 B．2‎ C．3 D．4‎ 解析　命题①不是真命题，因为底面是矩形，但侧棱不垂直于底面的平行六面体不是长方体；命题②不是真命题，因为底面是菱形(非正方形)，底面边长与侧棱长相等的直四棱柱不是正方体；命题③也不是真命题，因为有两条侧棱都垂直于底面一边不能推出侧棱与底面垂直；命题④是真命题，由对角线相等，可知平行六面体的对角面是矩形，从而推得侧棱与底面垂直，故平行六面体是直平行六面体．‎ 答案　A ‎5．(2012·北京东城11校联考)一个几何体的三视图如图所示，则此几何体的体积是 A．112 B．80‎ C．72 D．64‎ 解析　该几何体是由一个四棱锥与一个正方体拼接而成的，其中四棱锥的高为3、底面是边长为4的正方形，正方体的棱长为4，∴该几何体的体积为V＝×3×42＋43＝80.‎ 答案　B ‎6．一个空间几何体的三视图如图所示，则该几何体的表面积为 A．48 B．32＋8 C．48＋8 D．80‎ 解析 ‎　本题主要考查直四棱柱的三视图及四棱柱的表面积公式，由三视图可知该空间几何体是底面为等腰梯形的放倒的直四棱柱，如图所示，则该直四棱柱的表面积S＝2××(2＋4)×4＋4×4＋2×4＋2××4＝48＋8.‎ 答案　C 二、填空题(每小题5分，共15分)‎ ‎7．(2012·太原模拟)盛有水的圆柱形容器的内壁底面半径为‎5 cm，两个直径为‎5 cm的玻璃小球都浸没于水中，若取出这两个小球，则水面将下将________cm.‎ 解析　设水面将下降x cm，据题意知 π×52×x＝2×π×3，解得x＝cm.‎ 答案　 ‎8．三棱锥P－ABC中，PA⊥底面ABC，PA＝3，底面ABC是边长为2的正三角形，则三棱锥P－ABC的体积等于________．‎ 解析　∵PA⊥底面ABC，∴PA为三棱锥P－ABC的高，且PA＝3.‎ ‎∵底面ABC为正三角形且边长为2，‎ ‎∴底面面积为×22×sin 60°＝，‎ ‎∴VP－ABC＝××3＝.‎ 答案　 ‎9．(2012·包头二模)四棱锥P－ABCD的三视图如图所示，四棱锥P－ABCD的五个顶点都在一个球面上，E、F分别是棱AB、CD的中点，直线EF被球面所截得的线段长为2，则该球表面积为________．‎ 解析　∵直线EF被球面所截得的线段长为2，‎ 故AC＝2，∴AB＝2，‎ 设PC的中点为O，易证OP＝OC＝OA＝OB＝OD，‎ ‎∴O即为球心，则球的半径R＝，∴S＝12π.‎ 答案　12π 三、解答题(每小题12分，共36分)‎ ‎10．某商店门口标识墩的直观图以及正视图和俯视图如图所示，墩的上半部分是正四棱锥P－‎ EFGH，下半部分是长方体ABCD－EFGH.‎ ‎(1)请画出该标识墩的侧视图；‎ ‎(2)求该标识墩的体积．‎ 解析　(1)由于墩的上半部分是正四棱锥P－EFGH，下半部分是长方体ABCD－EFGH，故其侧视图与正视图全等．该标识墩的侧视图如图所示．‎ ‎(2)由三视图易得，长方体与正四棱锥的底面均是边长为‎40 cm的正方形，长方体的高为‎20 cm，正四棱锥的高为‎60 cm.‎ 故该标识墩的体积V＝VP－EFGH＋VABCD－EFGH＝×40×40×60＋40×40×20＝64 000(cm3)．‎ ‎11．已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．‎ ‎(1)若M为CB的中点，证明：MA∥平面CNB1；‎ ‎(2)求这个几何体的体积．‎ 解析　(1)证明　取CB1的中点P，连接MP，NP.‎ 因为M为CB的中点，所以MP∥BB1，且MP＝BB1.‎ 由三视图可知，四边形ABB1N为直角梯形，‎ AN∥BB1且AN＝BB1，则MP∥AN且MP＝AN，‎ 所以四边形ANPM为平行四边形，‎ 所以AM∥NP.‎ 又因为AM⊄平面CNB1，NP⊂平面CNB1，‎ 所以AM∥平面CNB1.‎ ‎(2)因为该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，所以BC⊥BA，BC⊥B1B.‎ 又BB1与BA相交于点B，连接BN，所以BC⊥平面ABB1N，‎ 所以BC为三棱锥C－ABN的高．‎ 取BB1的中点Q，连接QN，‎ 因为四边形ABB1N是直角梯形且AN＝BB1＝4，‎ 所以四边形ABQN为正方形，所以NQ⊥BB1，‎ 又BC⊥平面ABB1N，NQ⊂平面ABB1N，‎ 所以BC⊥NQ，又BC与BB1相交于点B，‎ 所以NQ⊥平面C1B1BC，所以NQ为四棱锥N－CBB1C1的高．‎ 所以该几何体的体积V＝VC－ABN＋VN－CBB1C1＝CB·S△ABN＋NQ·S四边形BCC1B1‎ ‎＝×4××4×4＋×4×4×8＝.‎ ‎12．一个空间几何体的三视图及部分数据如图所示，其正视图、俯视图均为矩形，侧视图为直角三角形．‎ ‎(1)请画出该几何体的直观图，并求出它的体积；‎ ‎(2)证明：A‎1C⊥平面AB‎1C1；‎ ‎(3)若D是棱CC1的中点，E是棱AB的中点，判断DE是否平行于平面AB‎1C1，并证明你的结论．‎ 解析　(1)几何体的直观图如图所示，‎ 四边形BB1C1C是矩形，BB1＝CC1＝，BC＝B1C1＝1，四边形AA1C1C是边长为的正方形，且平面AA1C1C垂直于底面BB1C1C，‎ 故该几何体是直三棱柱，其体积V＝S△ABC·BB1＝×1××＝.‎ ‎(2)证明　由(1)知平面AA‎1C1C⊥平面BB‎1C1C且B‎1C1⊥CC1，‎ 所以B1C1⊥平面ACC1A1，‎ 所以B1C1⊥A1C.‎ 因为四边形ACC1A1为正方形，所以A1C⊥AC1，‎ 而B1C1∩AC1＝C1，所以A1C⊥平面AB1C1.‎ ‎(3)DE∥平面AB‎1C1，证明如下：‎ 如图，取BB1的中点F，连接EF，DF，DE.‎ 因为D，E，F分别为CC1，AB，BB1的中点，‎ 所以EF∥AB1，DF∥B1C1.‎ 又AB1⊂平面AB1C1，EF⊄平面AB1C1，‎ 所以EF∥平面AB1C1.‎ 同理，DF∥平面AB1C1，‎ 又EF∩DF＝F，‎ 则平面DEF∥平面AB1C1.‎ 而DE⊂平面DEF，所以DE∥平面AB1C1.‎