2018-2019学年河南省河南大学附属中学高二下学期期中考试数学（文）试题（word版）

2018-2019学年河南省河南大学附属中学高二下学期期中考试数学（文）试题（word版）

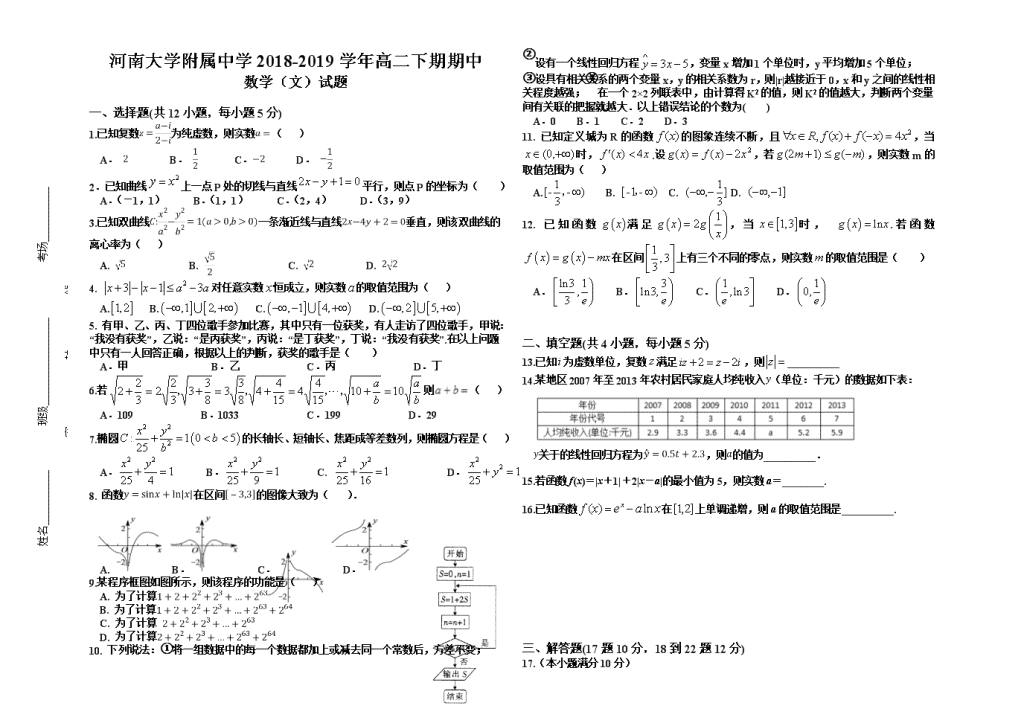
姓名 班级 考场 ‎ ‎………………………………………………密 …… 封 ……… 线……………………………………………………‎ 河南大学附属中学2018-2019学年高二下期期中 数学（文）试题 一、选择题(共12小题，每小题5分)‎ ‎1.已知复数为纯虚数，则实数（ ）‎ A． B． C． D． ‎ ‎2．已知曲线上一点P处的切线与直线平行，则点P的坐标为（ ）‎ A．（－1，1） B．（1，1） C．（2，4） D．（3，9）‎ ‎3.已知双曲线一条渐近线与直线垂直，则该双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎4. 对任意实数恒成立，则实数的取值范围为（ ）‎ A. B. C. D.‎ ‎5. 有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖，有人走访了四位歌手，甲说：“我没有获奖”，乙说：“是丙获奖”，丙说：“是丁获奖”，丁说：“我没有获奖”.在以上问题中只有一人回答正确，根据以上的判断，获奖的歌手是（ ）‎ A．甲 B．乙 C．丙 D．丁 ‎6.若则（ ）‎ A．109 B．1033 C．199 D．29‎ ‎7.椭圆的长轴长、短轴长、焦距成等差数列，则椭圆方程是（ ）‎ A． B． C. D．‎ ‎8. 函数在区间的图像大致为（ ）．‎ A. B． C． D．‎ ‎9.某程序框图如图所示，则该程序的功能是（ ）‎ A. 为了计算 ‎ B. 为了计算 C. 为了计算 ‎ D. 为了计算 ‎10. 下列说法：①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；‎ ‎②设有一个线性回归方程，变量x增加1个单位时，y平均增加5个单位；‎ ‎③设具有相关关系的两个变量x，y的相关系数为r，则|r|越接近于0，x和y之间的线性相关程度越强；④在一个2×2列联表中，由计算得K2的值，则K2的值越大，判断两个变量间有关联的把握就越大．以上错误结论的个数为(　　)‎ A．0 B．1 C．2 D．3‎ ‎11. 已知定义城为R的函数的图象连续不断，且，当时，.设，若，则实数m的取值范围为（ ）‎ A. B. C. D. ‎ ‎12. 已知函数满足，当时， .若函数在区间上有三个不同的零点，则实数的取值范围是（ ）‎ A． B． C． D．‎ 二、填空题(共4小题，每小题5分)‎ ‎13.已知为虚数单位，复数满足，则__________‎ ‎14.某地区2007年至2013年农村居民家庭人均纯收入（单位：千元）的数据如下表：‎ 关于的线性回归方程为，则的值为__________．‎ ‎15.若函数f(x)＝|x＋1|＋2|x－a|的最小值为5，则实数a＝________.‎ ‎16.已知函数在上单调递增，则a的取值范围是__________.‎ 三、解答题(17题10分，18到22题12分)‎ ‎17.（本小题满分10分）‎ 若,,,求证:不能同时大于1.‎ ‎18. （本小题满分12分）‎ 已知函数.‎ ‎(1)在答题卡中画出的图像；‎ ‎(2)求不等式的解集．‎ ‎19. （本小题满分12分）‎ 已知函数 ‎(1)讨论函数的单调区间；‎ ‎(2)当时，若函数在区间上的最大值为3，求的取值范围 ‎20. （本小题满分12分）‎ 设椭圆的右顶点为,上顶点为.已知椭圆的焦距为,直线的斜率为.‎ ‎(1)求椭圆的标准方程；‎ ‎(2)设直线（）与椭圆交于M，N两点，且点M在第二象限.与延长线交于点，若的面积是面积的3倍，求k的值.‎ ‎21. （本小题满分12分）‎ 为打赢脱贫攻坚战，解决脱贫问题，政府重点扶持扶贫工厂.当地对某扶贫工厂进行设备改造，为分析设备改造前后的效果，现从设备改造前后生产的大量产品中各抽取100件产品作为样本，检测质量指标值.该产品为次品、合格品、优等品所对应的指标值范围分别为[35,55],[55,75],[75,85].设备改造前的样本的频率分布直方图如图所示，设备改造后的样本的频数分布表如下所示.‎ ‎(1)根据以上数据，完成以下列联表，并判断是否有的把握认为设备改造与产品为次品有关？‎ ‎(2)若工人的月工资是由基本工资1000元与效益工资两部分组成.效益工资实施细则如下：每生产一件产品是合格品的奖50元，是优等品的奖100元，是次品的扣20元.将频率视为概率，估计设备改造后，一个月生产60件产品的工人月工资为多少元？‎ 附：‎ ‎22. （本小题满分12分）‎ 已知函数(为常数)，曲线在与轴的交点处的切线斜率为.‎ ‎(1)求的值及函数的单调区间；‎ ‎(2)证明：当时，‎ 文科答案 一、选择题:DBACA ACAAC AA 二、填空题: 或 ‎ 三、解答题 ‎17.(反证法)假设结论不成立，即同时大于.‎ 而 这与矛盾.‎ 所以假设错误，即不能同时大于. ‎ ‎18.‎ ‎19.试题解析：（I）． 1分 令得． 2分 ‎（i）当，即时， ， 在单调递增． 3分 ‎（ii）当，即时，‎ 当时， 在内单调递增；‎ 当时， 在内单调递减． 4分 ‎（iii）当，即时，‎ 当时， 在内单调递增；‎ 当时， 在内单调递减． 5分 综上，当时， 在内单调递增， 在内单调递减；‎ 当时， 在单调递增；‎ 当时， 在内单调递增，‎ 在内单调递减．（其中） 6分 ‎（II）当时， ， ‎ 令，得． 7分 将， ， 变化情况列表如下：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎1 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎0 ‎ ‎ ‎ ‎0 ‎ ‎ ‎ ‎ ‎ ‎↗ ‎ 极大 ‎ ‎↘ ‎ 极小 ‎ ‎↗ ‎ ‎8分 由此表可得， ． 9分 又， 10分 故区间内必须含有，即的取值范围是． 12分 ‎20. 【详解】解：（1）设椭圆的焦距为，由已知得，‎ 所以，，所以椭圆的方程为.‎ ‎（2）设点，，由题意，且，‎ 由的面积是面积的倍，可得，‎ 所以，从而，‎ 所以，即.‎ 易知直线的方程为，由，消去，可得.‎ 由方程组，消去，可得.‎ 由，可得，‎ 整理得，解得或.‎ 当时，，符合题意；当时，，不符合题意，舍去.‎ 综上，的值为.‎ ‎21. ‎ ‎22.试题解析：（1）由，得．‎ 又，所以．所以，．‎ 由，得．‎ 所以函数在区间上单调递减，在上单调递增． （4分）‎ ‎（2）首先证明：当时，恒有．证明如下：令，则．由（2）知，当时，，所以，所以在上单调递增，所以，所以．所以，即．‎ 依次取，代入上式，则，，‎ ‎．以上各式相加，有 所以，‎ 所以，即（12分）‎