高一必修1典例选讲及配套习题 第5讲 集合复习

高一必修1典例选讲及配套习题 第5讲 集合复习

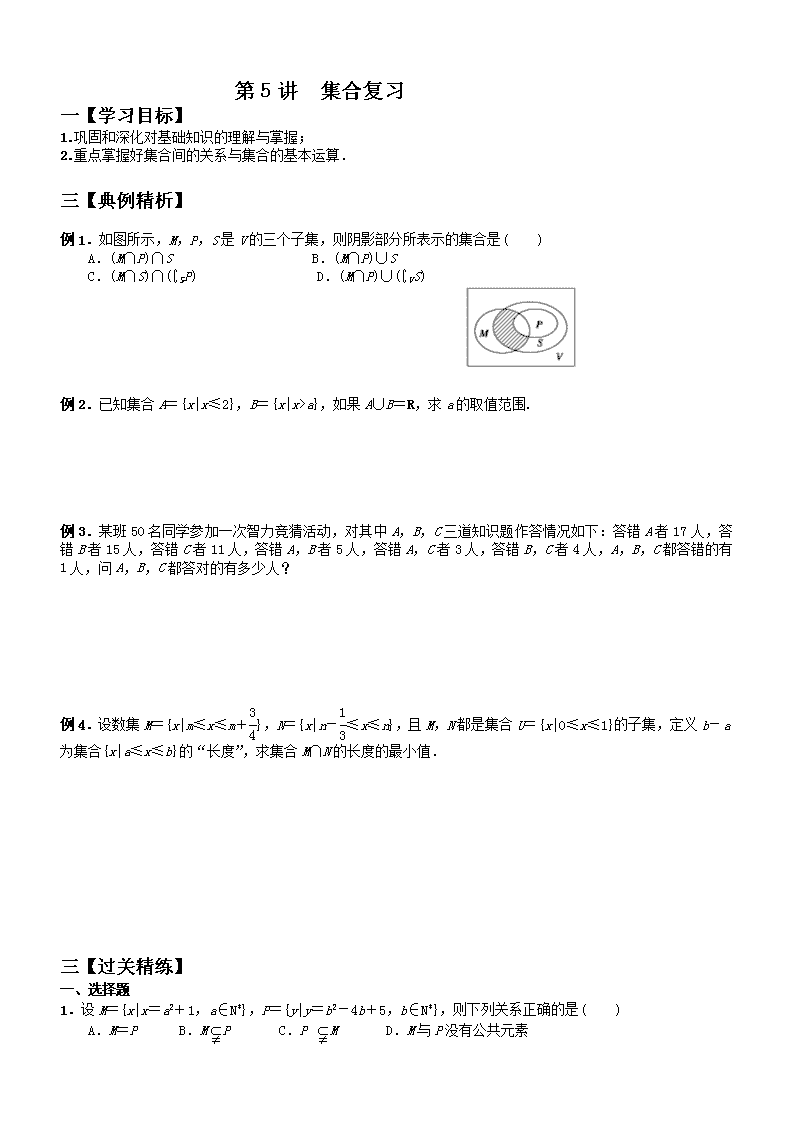
第5讲 集合复习 一【学习目标】‎ ‎1.巩固和深化对基础知识的理解与掌握；‎ ‎2.重点掌握好集合间的关系与集合的基本运算．‎ 三【典例精析】‎ 例1．如图所示，M，P，S是V的三个子集，则阴影部分所表示的集合是( )‎ A．(M∩P)∩S B．(M∩P)∪S C．(M∩S)∩(∁SP) D．(M∩P)∪(∁VS)‎ ‎ ‎ 例2．已知集合A＝{x|x≤2}，B＝{x|x>a}，如果A∪B＝R，求a的取值范围.‎ 例3．某班50名同学参加一次智力竞猜活动，对其中A，B，C三道知识题作答情况如下：答错A者17人，答错B者15人，答错C者11人，答错A，B者5人，答错A，C者3人，答错B，C者4人，A，B，C都答错的有1人，问A，B，C都答对的有多少人？‎ ‎ ‎ 例4．设数集M＝{x|m≤x≤m＋}，N＝{x|n－≤x≤n}，且M，N都是集合U＝{x|0≤x≤1}的子集，定义b－a为集合{x|a≤x≤b}的“长度”，求集合M∩N的长度的最小值．‎ 三【过关精练】‎ 一、选择题 ‎1．设M＝{x|x＝a2＋1，a∈N*}，P＝{y|y＝b2－4b＋5，b∈N*}，则下列关系正确的是( )‎ A．M＝P B．MP C．P M D．M与P没有公共元素 ‎2．方程组的解构成的集合是（ ）‎ A． B． C．（1，1） D．‎ ‎3．已知集合A={a，b，c},下列可以作为集合A的子集的是（ ）‎ A.a B.{a，c} C.{a，e} D.{a，b，c，d}‎ ‎4．下列图形中，表示的是（ ）‎M N D N M C M N B M N A ‎5．下列表述正确的是（ ）‎ A. B. C. D. ‎ ‎6.设集合A＝{x|x参加自由泳的运动员}，B＝{x|x参加蛙泳的运动员}，对于“既参 加自由泳又参加蛙泳的运动员”用集合运算表示为( )‎ A.A∩B B.AB C.A∪B D.AB ‎7.符合条件{a}P⊆{a，b，c}的集合P的个数是( )‎ A．2 B．3 C．4 D．5‎ ‎8.集合A={1，2，x}，集合B={2，4，5}，若={1，2，3，4，5}，则x=（ ）‎ A.1 B.3 C.4 D.5‎ ‎9.满足条件{1,2,3}M{1,2,3,4,5,6}的集合M的个数是（ ）‎ A.8 B.7 C.6 D.5‎ ‎10.全集U = {1，2，3，4，5，6，7，8}，A= {3，4，5}， B= {1，3，6}，那么 集合{2，7，8}是 （ ）‎ A. B. C. D.‎ ‎11.设集合， ( )‎ A． B． C． D．‎ ‎12.如果集合A={x|ax2＋2x＋1=0}中只有一个元素，则a的值是（ ）‎ A．0 B．0或1 C．1 D．不能确定 二、填空题 ‎13．用描述法表示被3除余1的整数的集合 ．‎ ‎14．用适当的符号填空：‎ ‎（1） ； （2）{1，2，3} N；‎ ‎（3）{1} ； （4）0 ．‎ ‎15.含有三个实数的集合既可表示成，又可表示成，则 .‎ ‎16.已知集合，，那么集合 ， ， .‎ 三、解答题 ‎17.已知集合，集合，若，求实数a的取值集合．‎ ‎18.已知集合，集合，若满足 ，‎ 求实数a的值．‎ ‎19．已知集合A＝{x|－1≤x<3}，B＝{x|2x－4≥x－2}．‎ ‎(1)求A∩B；‎ ‎(2)若集合C＝{x|2x＋a>0}，满足B∪C＝C，求实数a的取值范围．‎ ‎20. 已知集合，，，若满足，求实数a的取值范围．‎ 参考答案 例1解：选C。阴影部分是M∩S的部分再去掉属于集合P的一小部分，因此为(M∩S)∩(∁SP)．‎ 例2解：如图中的数轴所示：‎ 要使A∪B＝R，a≤2.‎ 例3解：由题意，设全班同学为全集U，画出Venn图，A表示答错A的集合，B表示答错B 的集合，C表示答错C的集合，将其集合中元素数目填入图中，自中心区域向四周的各区域数目分别为1,2,3,4,10,7,5，因此A∪B∪C中元素数目为32，从而至少错一题的共32人，因此A，B，C全对的有50－32＝18人．‎ 例4解：在数轴上表示出集合M与N，可知当m＝0且n＝1或n－＝0且m＋＝1时，M∩N 的“长度”最小．当m＝0且n＝1时，M∩N＝{x|≤x≤}，长度为－＝；当n＝且m＝时，M∩N＝{x|≤x≤}，长度为－＝.综上，M∩N的长度的最小值为.‎ 一、选择题 ‎1.C；2.A；3.B；4.C；5.B；6.C；7.B；8.B；9.C；10.C；11.B；12.B.‎ 二、填空题 ‎13.,‎ ‎14.（1）；（2）{1，2，3}N；（3）{1}；（4）0；15.-1‎ ‎16.或；；‎ 或.‎ 三、解答题 ‎17.{0.-1,1}；‎ ‎18.；‎ ‎19.(1)∵B＝{x|x≥2}，∴A∩B＝{x|2≤x<3}．‎ ‎(2)∵C＝{x|x>－}，B∪C＝C⇔B⊆C，∴－<2，∴a>－4.‎ ‎20.．‎