2015广州一模数学(理)含答案

2015广州一模数学(理)含答案

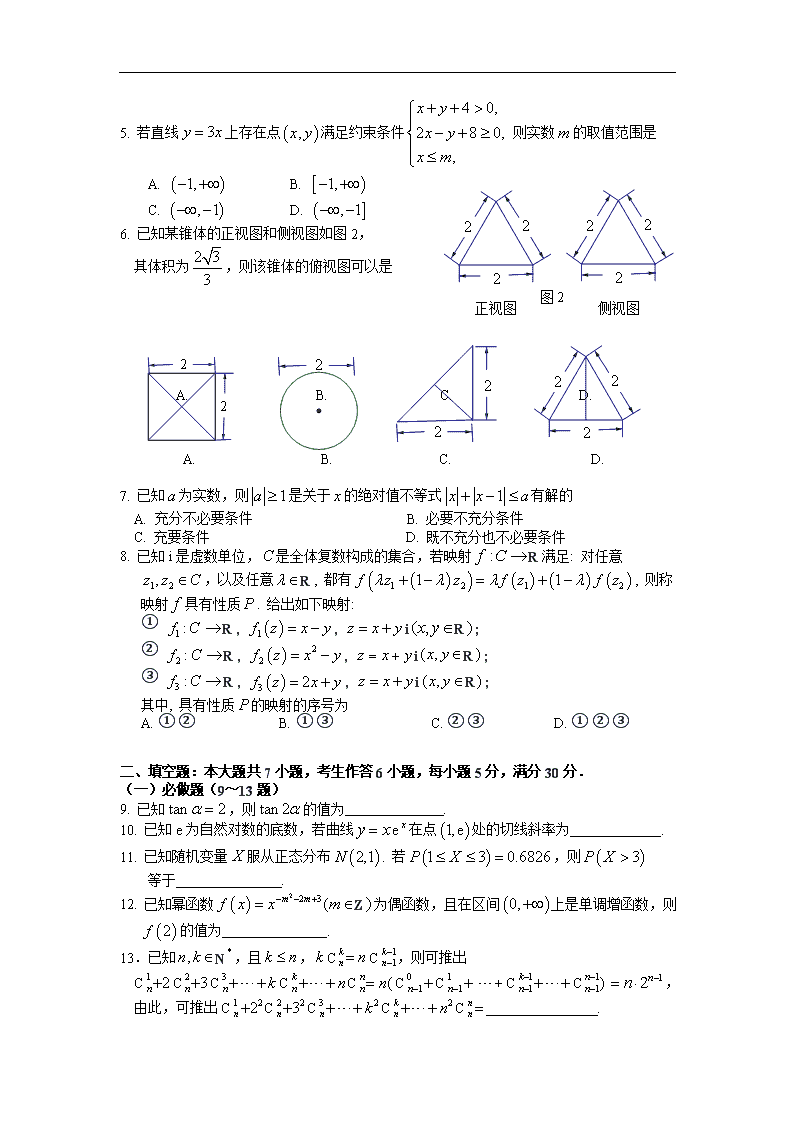
试卷类型：A ‎2015年广州市普通高中毕业班综合测试（一）‎ 数学（理科）‎ ‎ 2015.3‎ 本试卷共4页，21小题， 满分150分．考试用时120分钟.‎ 注意事项：‎ ‎1．答卷前，考生务必用2B铅笔在“考生号”处填涂考生号。用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型（A）填涂在答题卡相应位置上。‎ ‎2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。‎ ‎3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。‎ ‎4．作答选做题时，请先用2B铅笔填涂选做题题号对应的信息点，再作答。漏涂、错涂、多涂的，答案无效。‎ ‎5．考生必须保持答题卡的整洁。考试结束后，将试卷和答题卡一并交回。‎ 参考公式：锥体的体积公式，其中是锥体的底面积，是锥体的高．‎ ‎ ．‎ 一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 已知全集, 集合, , 则集合可以表示为 ‎ A． B． C． D．‎ ‎2．已知向量，若，则实数的值为 A． B． C． D．‎ ‎3. 若某市所中学参加中学生合唱比赛的得分用茎叶图表示（如图），其中茎为十位数，‎ ‎ 叶为个位数，则这组数据的中位数和平均数分别是 ‎ A. , B. , ‎ ‎ C. , D. , ‎ ‎4. 直线与圆的位置关系是 ‎ A. 相交 B. 相切 C. 相离 D. 不能确定 ‎5. 若直线上存在点满足约束条件 则实数的取值范围是 A. B. ‎ ‎ C. D. ‎ ‎6. 已知某锥体的正视图和侧视图如图2，‎ ‎ 其体积为，则该锥体的俯视图可以是 ‎ 图2‎ ‎ ‎ ‎ ‎ ‎ A. B. C. D.‎ A. B. C. D.‎ ‎7. 已知为实数，则是关于的绝对值不等式有解的 A. 充分不必要条件 B. 必要不充分条件 ‎ C. 充要条件 D. 既不充分也不必要条件 ‎ ‎8. 已知i是虚数单位，是全体复数构成的集合，若映射R满足: 对任意 ‎，以及任意R , 都有, 则称 映射具有性质. 给出如下映射:‎ ‎① R , , iR;‎ ‎② R , , iR;‎ ‎③ R , , iR;‎ 其中, 具有性质的映射的序号为 A. ① ② B. ① ③ C. ② ③ D. ① ② ③‎ 二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．‎ ‎（一）必做题（9～13题）‎ ‎9. 已知，则的值为 . ‎ ‎10. 已知e为自然对数的底数，若曲线e在点处的切线斜率为 . ‎ ‎11. 已知随机变量服从正态分布. 若，则 ‎ 等于 . ‎ ‎12. 已知幂函数Z为偶函数，且在区间上是单调增函数，则 ‎ 的值为 .‎ ‎13．已知N，且，CC，则可推出 CCCCCCCCC，‎ 由此，可推出CCCCC .‎ ‎（二）选做题（14～15题，考生只能从中选做一题） ‎ ‎14. （坐标系与参数方程选做题）‎ 在直角坐标系中，曲线和的参数方程分别为为参数和 为参数.以原点为极点，轴正半轴为极轴，建立极坐标系，则曲线 与的交点的极坐标为 . ‎ ‎15. （几何证明选讲选做题）‎ 如图3，是圆的一条弦，延长至点，‎ 使得，过作圆的切线，为 切点，的平分线交于点，‎ 则的长为 .‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎16．（本小题满分分）‎ 已知函数的图象在轴右侧的第一个最高点和第一个最低点的坐标分别为和.‎ ‎（1）求函数的解析式；‎ ‎（2）求的值.‎ ‎17. （本小题满分分）‎ 袋子中装有大小相同的白球和红球共个，从袋子中任取个球都是白球的概率为，每个球被取到的机会均等. 现从袋子中每次取个球，如果取出的是白球则不再放回，设在取得红球之前已取出的白球个数为.‎ ‎（1）求袋子中白球的个数；‎ ‎（2）求的分布列和数学期望.‎ ‎18. （本小题满分分）‎ 如图4，在边长为的菱形中，‎ ‎，点，分别是边，‎ 的中点，，沿将 ‎△翻折到△，连接，‎ 得到如图5的五棱锥，‎ 且.‎ ‎（1）求证：平面；‎ ‎（2）求二面角的正切值.‎ ‎ ‎ ‎19. （本小题满分分）‎ 已知数列的各项均为正数，其前项和为，且满足，N.‎ ‎（1）求的值；‎ ‎（2）求数列的通项公式；‎ ‎（3）是否存在正整数, 使, , 成等比数列? 若存在, 求的值； 若不存在, ‎ ‎ 请说明理由.‎ ‎20. （本小题满分分）‎ 已知椭圆的中心在坐标原点，两焦点分别为双曲线的顶点，直线与椭圆交于，两点，且点的坐标为，点是椭圆上异于点,的任意一点，点满足，，且，，三点不共线.‎ (1) 求椭圆的方程；‎ (2) 求点的轨迹方程；‎ (3) 求面积的最大值及此时点的坐标.‎ ‎21. （本小题满分分）‎ 已知函数.‎ ‎（1）若对都成立，求的取值范围；‎ ‎（2）已知为自然对数的底数，证明：N，.‎ 数学（理科）参考答案 说明：1．参考答案与评分标准给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力比照评分标准给以相应的分数．‎ ‎ 2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．‎ ‎ 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ ‎4．只给整数分数，选择题和填空题不给中间分．‎ 一、选择题：本大题考查基本知识和基本运算．共8小题，每小题5分，满分40分． ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B D C A A C B B ‎ ‎ 二、填空题：本大题考查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．‎ ‎9. 10. 11. 12. 13. ‎ ‎14. 15. ‎ 说明: 第题答案可以是Z .‎ 三、解答题：本大题共6小题，满分80分．‎ ‎16．（本小题满分12分）‎ ‎（本小题主要考查三角函数的图象与性质、三角两角和公式等等知识，考查化归与转化的数学思想方法，以及运算求解能力）‎ ‎（1）解：由题意可得， …………………………1分 ‎ ， …………………………3分 ‎ ∴ …………………………4分 ‎ 由得， …………………………5分 ‎ ∴. …………………………6分 ‎（2）解： ∵ 点是函数在轴右侧的第一个最高点,‎ ‎ ∴ . …………………………7分 ‎ ∴ . …………………………8分 ‎ ∴ …………………………9分 ‎ …………………………10分 ‎ …………………………11分 ‎ . …………………………12分 ‎17．（本小题满分12分）‎ ‎（本小题主要考查古典概型、解方程、随机变量的分布列与均值（数学期望）等知识，考查或然与必然的数学思想方法，以及数据处理能力、运算求解能力和应用意识）‎ ‎（1）解：设袋子中有N个白球，依题意得，，………………………1分 即， 化简得，， …………………………2分 ‎ 解得，或（舍去）. …………………………3分 ‎ ∴袋子中有个白球. …………………………4分 ‎（2）解：由（1）得，袋子中有个红球，个白球. …………………………5分 ‎ 的可能取值为， …………………………6分 ‎ ， ，‎ ‎ ，. ………………10分 ‎ ∴的分布列为：‎ ‎ ‎ ‎ …………………………11分 ‎ ∴. …………………………12分 ‎18．（本小题满分14分）‎ ‎（本小题主要考查空间线面关系、二面角、空间向量及坐标运算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力）‎ ‎（1）证明：∵点，分别是边，的中点，‎ ‎ ∴∥. …………………………1分 ‎ ∵菱形的对角线互相垂直，‎ ‎ ∴.‎ ‎ ∴.‎ ‎ ∴，. …………………………2分 ‎ ∵平面，平面，，‎ ‎ ∴平面. …………………………3分 ‎ ∴平面. …………………………4分 ‎（2）解法1：设，连接，‎ ‎ ∵，‎ ‎ ∴△为等边三角形.‎ ‎ ∴，，，. ……5分 ‎ 在R t△中，，‎ ‎ 在△中，，‎ ‎ ∴. …………………………6分 ‎ ∵，，平面，平面，‎ ‎ ∴平面. …………………………7分 ‎ 过作，垂足为，连接，‎ ‎ 由（1）知平面，且平面，‎ ‎ ∴.‎ ‎ ∵，平面，平面，‎ ‎ ∴平面. …………………………8分 ‎ ∵平面，‎ ‎ ∴. …………………………9分 ‎ ∴为二面角的平面角. …………………………10分 ‎ 在Rt△中，，‎ ‎ 在Rt△和Rt△中，，‎ ‎ ∴Rt△～Rt△. …………………………11分 ‎ ∴.‎ ‎ ∴. …………………………12分 ‎ 在Rt△中， . ……………………13分 ‎ ∴二面角的正切值为. …………………………14分 解法2：设，连接，‎ ‎ ∵，‎ ‎ ∴△为等边三角形.‎ ‎ ∴，，，.………………………5分 ‎ 在R t△中，，‎ ‎ 在△中，，‎ ‎ ∴. …………………………6分 ‎ ∵，，平面，平面，‎ ‎ ∴平面. …………………………7分 ‎ 以为原点，所在直线为轴，所在直线为轴，所在直线为轴，‎ ‎ 建立空间直角坐标系，‎ ‎ 则，，，.…………8分 ‎ ∴，.‎ ‎ 设平面的法向量为，‎ ‎ 由，，得 ……9分 ‎ 令，得，.‎ ‎ ∴平面的一个法向量为. …………………………10分 ‎ 由（1）知平面的一个法向量为， ……………………11分 ‎ 设二面角的平面角为，‎ ‎ 则.………………………12分 ‎ ∴，.………………………13分 ‎ ∴二面角的正切值为. …………………………14分 ‎19．（本小题满分14分）‎ ‎（本小题主要考查等差数列、数列的前项和等知识，考查化归与转化的数学思想方法，以及运算求解能力和创新意识）‎ ‎（1）解：∵，‎ ‎∴. …………………………1分 ‎（2）解法1：由，得， …………………………2分 故. …………………………3分 ‎∵，∴.‎ ‎∴. …………………………4分 ‎∴数列是首项为，公差为的等差数列.‎ ‎∴. …………………………5分 ‎∴. …………………………6分 当时，， …………………………8分 又适合上式，‎ ‎∴. …………………………9分 解法2：由，得， …………………………2分 ‎ 当时，，　　　　　　　　　　…………………………3分 ‎ ∴. …………………………４分 ‎∴. ‎ ‎∴. …………………………５分 ‎∵ ，‎ ‎∴. …………………………６分 ‎∴数列从第2项开始是以为首项，公差为的等差数列．……………７分 ‎∴．　　　　　　　　…………………………８分 ‎∵适合上式，‎ ‎∴. …………………………9分 解法3：由已知及（1）得，，‎ ‎ 猜想. …………………………2分 ‎ 下面用数学归纳法证明.‎ ‎① 当，时，由已知，，猜想成立. ………3分 ‎② 假设时，猜想成立，即， …………………………4分 ‎ 由已知，得， ‎ ‎ 故. ‎ ‎ ∴. …………………………5分 ‎ ∴.‎ ‎ ∴. …………………………6分 ‎ ∵，‎ ‎ ∴. …………………………7分 ‎ ∴. …………………………8分 ‎ 故当时，猜想也成立.‎ ‎ 由①②知，猜想成立，即. …………………………9分 ‎（3）解：由(2)知, .‎ ‎ 假设存在正整数, 使, , 成等比数列,‎ ‎ 则. …………………………10分 ‎ 即. …………………………11分 ‎ ∵ 为正整数，‎ ‎ ∴ .‎ ‎ ∴ .‎ ‎ ∴ .‎ ‎ 化简得 . …………………………12分 ‎ ∵ ,‎ ‎ ∴ .‎ ‎ 解得, 与为正整数矛盾. ……………………13分 ‎∴ 不存在正整数, 使, , 成等比数列. …………………………14分 ‎20.（本小题满分14分）‎ ‎（本小题主要考查椭圆的方程、双曲线的方程、直线与圆锥曲线的位置关系等知识，考查数形结合、化归与转化、函数与方程的数学思想方法，以及推理论证能力和运算求解能力）‎ ‎（1）解法1： ∵ 双曲线的顶点为,, …………1分 ‎∴ 椭圆两焦点分别为,. ‎ 设椭圆方程为，‎ ‎∵ 椭圆过点，‎ ‎∴ ，得. ………………………2分 ‎∴ . ………………………3分 ‎∴ 椭圆的方程为 . ………………………4分 解法2: ∵ 双曲线的顶点为,, ……………………1分 ‎∴ 椭圆两焦点分别为,. ‎ 设椭圆方程为，‎ ‎∵ 椭圆过点，‎ ‎∴ . ① ………………………2分 ‎. ∵ , ② ………………………3分 由①②解得, .‎ ‎∴ 椭圆的方程为 . ………………………4分 ‎（2）解法1：设点，点，‎ 由及椭圆关于原点对称可得，‎ ‎∴，，‎ ‎，.‎ 由 , 得 ， ……………………5分 即 . ①‎ 同理, 由, 得 . ② ……………6分 ‎ ①②得 . ③ ………………………7分 由于点在椭圆上, 则，得,‎ 代入③式得 . ‎ 当时，有， ‎ 当，则点或,此时点对应的坐标分别为或 ‎ ，其坐标也满足方程. ………………………8分 当点与点重合时，即点，由②得 ，‎ 解方程组 得点的坐标为或.‎ 同理, 当点与点重合时，可得点的坐标为或.‎ ‎∴点的轨迹方程为 , 除去四个点,, ,‎ ‎. ………………………9分 解法2：设点，点，‎ 由及椭圆关于原点对称可得，‎ ‎∵，， ∴，.‎ ‎ ∴，① ……………………5分 ‎ . ② ……………………6分 ‎ ‎①② 得 . (*) ………………………7分 ‎∵ 点在椭圆上, ∴ ，得,‎ 代入(*)式得，即, 化简得 . ‎ ‎ 若点或, 此时点对应的坐标分别为或 ‎ ，其坐标也满足方程. ………………………8分 当点与点重合时，即点，由②得 ，‎ 解方程组 得点的坐标为或.‎ 同理, 当点与点重合时，可得点的坐标为或.‎ ‎∴点的轨迹方程为 , 除去四个点,, ,‎ ‎. ………………………9分 ‎(3) 解法１：点到直线的距离为.‎ ‎△的面积为………………………10分 ‎ . ………………………11分 ‎ 而（当且仅当时等号成立）‎ ‎∴. ……12分 当且仅当时, 等号成立.‎ 由解得或 ………………………13分 ‎∴△的面积最大值为, 此时,点的坐标为或.…14分 解法２：由于，‎ 故当点到直线的距离最大时，△的面积最大．………………………1０分 设与直线平行的直线为，‎ 由消去，得， ‎ 由，解得．　　　………………………1１分 若，则，；若，则，．…1２分 故当点的坐标为或时，△的面积最大，其值为 ‎．　　　　　　　　　　………………………1４分 ‎21．（本小题满分14分）‎ ‎（本小题主要考查函数的导数、不等式等知识，考查数形结合、化归与转化、分类与讨论的数学思想方法，以及运算求解能力、抽象概括能力与创新意识）‎ ‎（1）解：∵，其定义域为,‎ ‎ ∴. …………………………1分 ‎ ① 当时，，当时，，‎ ‎ 则在区间上单调递减，此时，，不符合题意. …2分 ‎ ② 当时，令，得，，‎ ‎ 当时，，则在区间上单调递减，‎ ‎ 此时，，不符合题意. …………………………3分 ‎ ③ 当时，，当时，，‎ ‎ 则在区间上单调递增，此时，，符合题意. ……4分 ‎ ④ 当时，令，得，，当时，，‎ ‎ 则在区间上单调递增，此时，，符合题意. ……5分 ‎ 综上所述，的取值范围为. …………………………6分 ‎（2）证明：由（1）可知，当时，对都成立，‎ ‎ 即对都成立. …………………………7分 ‎ ∴.………………8分 ‎ 即.‎ ‎ 由于N，则. …………………………9分 ‎ ∴. ‎ ‎ ∴ . …………………………10分 ‎ 由（1）可知，当时，对都成立，‎ ‎ 即对都成立. …………………………11分 ‎ ∴.‎ ‎ …………………………12分 ‎ 即.‎ ‎ 得 ‎ 由于N，则.‎ ‎…………………………13分 ‎ ∴.‎ ‎ ∴ . …………………………14分 ‎ ∴‎