2017-2018学年四川省泸州老窖天府中学高二上学期期中考试数学试题 缺答案

2017-2018学年四川省泸州老窖天府中学高二上学期期中考试数学试题 缺答案

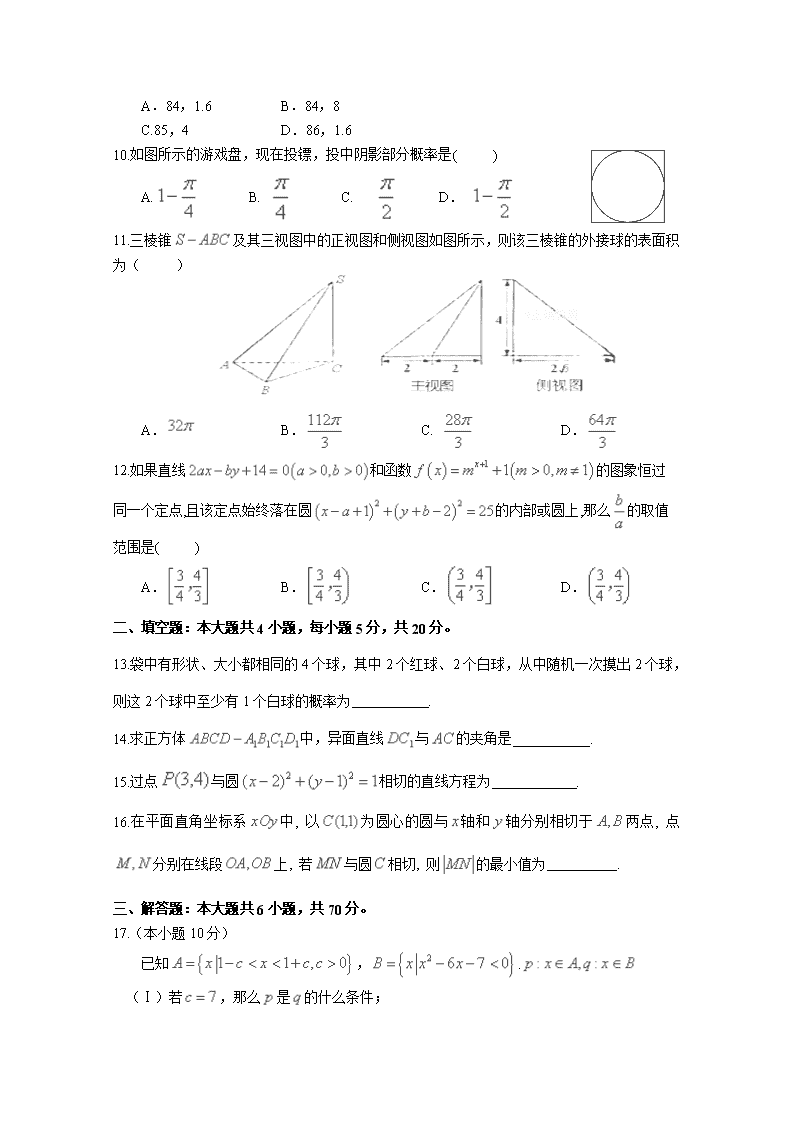
‎2017-2018学年四川省泸州老窖天府中学高二上学期期中考试 数 学 一、选择题：本大题共12小题，每小题5分，共60分。‎ ‎1.直线，在轴上的截距是 ( ) ‎ A．0 B．-1 C．1 D．2‎ ‎2.命题“”的否定是（ ）‎ A． B． C． D．‎ ‎3.某企业共有职工150人，其中高级职称15人，中级职称45人，初级职称90人．现采用分层抽样抽取容量为30的样本，则抽取的各职称的人数分别为(　 　)‎ A．5,10,15 B．3,9,18 C．3,10,17 D．5,9,16‎ ‎4.有人收集了春节期间平均气温与某取暖商品销售额的有关数据如下表：‎ 平均气温(℃)‎ ‎－2‎ ‎－3‎ ‎－5‎ ‎－6‎ 销售额(万元)‎ ‎20‎ ‎23‎ ‎27‎ ‎30‎ 则该商品销售额与平均气温有：‎ A.确定性关系 B.正相关关系 C.负相关关系 D.函数关系 ‎5.圆和圆的位置关系为（ ）‎ A.相交 B.外切 C.内切 D.相离 ‎6.已知是相异两平面，是相异两直线，则下列命题中不正确的是 （　 　）‎ A.若，则    B.若，则 C.若，则 D.若，则 ‎7.“”是“”的（ ）条件 A. 充要 B. 充分不必要 ‎ C. 必要不充分 D. 既不充分也不必要 ‎8.公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3．14，这就是著名的“徽率”．如右图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为( )‎ A．6 B．12 C．24 D．25‎ ‎9.某中学举行英语演讲比赛，如图是七位评委为某位学生打出分数的茎叶图，去掉一个最高分和一个最低分，所剩数据的中位数和方差分别为（ ）‎ A．84，1.6 B．84，8 ‎ C.85，4 D．86，1.6 ‎ ‎10.如图所示的游戏盘，现在投镖，投中阴影部分概率是( )‎ A. B. C. D． ‎ ‎11.三棱锥及其三视图中的正视图和侧视图如图所示，则该三棱锥的外接球的表面积为（ ）‎ A． B． C. D．‎ ‎12.如果直线和函数的图象恒过同一个定点,且该定点始终落在圆的内部或圆上,那么的取值范围是( )‎ A． B． C． D．‎ 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎13.袋中有形状、大小都相同的4个球，其中2个红球、2个白球，从中随机一次摸出2个球，则这2个球中至少有1个白球的概率为 . ‎ ‎14.求正方体中，异面直线与的夹角是 .‎ ‎15.过点与圆相切的直线方程为 .‎ ‎16.在平面直角坐标系中, 以为圆心的圆与轴和轴分别相切于两点, 点分别在线段上, 若与圆相切, 则的最小值为 .‎ 三、解答题：本大题共6小题，共70分。‎ ‎17.（本小题10分）‎ 已知，.‎ ‎（Ⅰ）若，那么是的什么条件；‎ ‎（Ⅱ）若是的充分不必要条件，求的取值范围．‎ ‎18.（本小题10分）某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为 ，……， ‎（Ⅰ）求频率分布图中的值；‎ ‎（Ⅱ）估计该企业的职工对该部门评分不低于80的概率；‎ ‎（Ⅲ）从评分在的受访职工中，随机抽取2人，求这2人评分都在的概率.‎ ‎19.（本小题12分）已知圆过原点且与直线相切，且圆心在直线上．‎ ‎（Ⅰ）求圆的方程；‎ ‎（Ⅱ）过点的直线与圆相交于两点,且,求直线的方程．‎ ‎20.（本小题12分）某零售店1~5月的销售额和利润额资料如下表所示：‎ 月份 一月 二月 三月 四月 五月 销售额/千万元 ‎3‎ ‎5‎ ‎6‎ ‎7‎ ‎9‎ 利润额/百万元 ‎2‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎（Ⅰ）求利润额关于销售额的线性回归方程；‎ ‎（Ⅱ）利用（Ⅰ ‎）中的回归方程，预测当销售额为4千万元时，该零售店的利润额(百万元)．‎ 附：回归直线的斜率和截距的最小二乘法估计公式分别为：‎ ‎，.‎ ‎21.（本小题12分）如图，直棱柱中，分别是的中点，‎ ‎（Ⅰ）证明：‎ ‎（Ⅱ）若,.‎ ‎（理）求二面角的正弦值.‎ ‎（文）求三棱锥的体积.‎ ‎22.（本小题14分）在平面直角坐标系中，已知半径为的圆，圆心在轴正半轴上，且与直线相切.‎ ‎（1）求圆的方程；‎ ‎（2）在圆上，是否存在点，满足，其中，点的坐标是.若存在，指出有几个这样的点；若不存在，请说明理由；‎ ‎（3）若在圆上存在点，使得直线与圆相交于不同两点，求的取值范围.并求出使得的面积最大的点的坐标及对应的的面积. ‎