2018届二轮复习规范答题大题突破课数列、不等式、推理与证明课件理

2018届二轮复习规范答题大题突破课数列、不等式、推理与证明课件理

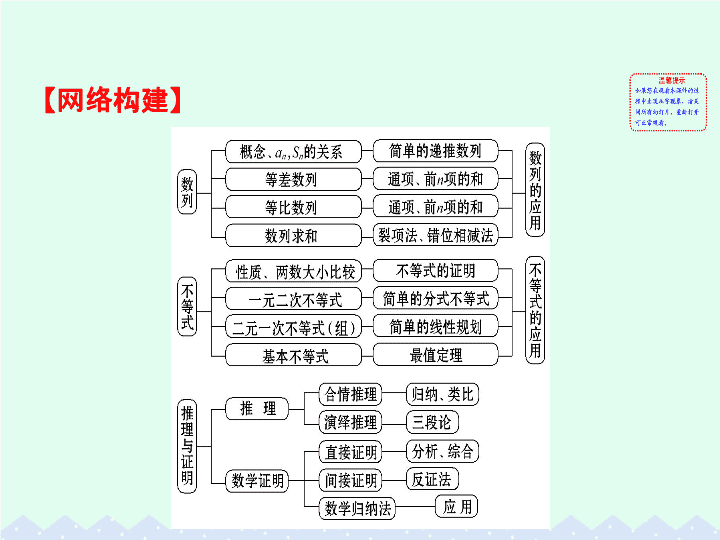
阶段总结 · 热考题型强化课 ( 三 ) 数列、不等式、推理与证明 【 网络构建 】 【 核心要素 】 1. 不等式的性质及应用 2. 一元二次不等式的解法 3. 简单线性规划、可行域、最优解 4. 基本不等式适用条件及利用基本不等式求最值 5.a n ,S n 的关系及应用 6. 等差数列、等比数列通项及前 n 项和 7. 等差数列、等比数列的性质 8. 求和的两种基本方法 : 裂项法及错位相减法 9. 推理 : 归纳推理、类比推理、演绎推理 10. 证明方法 : 分析法、综合法、反证法的具体方法步骤 11. 数学归纳法的方法步骤 热考题型一 　等差数列、等比数列基本量的计算及性质应用 【 考情分析 】 难度 : 基础题 题型 : 以选择题、填空题为主 考查方式 : 以数列首项 , 公差 ( 公比 ), 通项公式、前 n 项和及性质为考查对象 , 有时与二次函数、一元二次方程结合考查 【 考题集训 】 1.(2015· 重庆高考 ) 在等差数列 {a n } 中 , 若 a 2 =4,a 4 =2, 则 a 6 = 　 ( 　　 ) A.-1 B.0 C.1 D.6 【 解析 】 选 B. 因为数列 {a n } 为等差数列 , 所以 a 4 为 a 2 和 a 6 的等差中项 , 所以有 2a 4 =a 2 +a 6 , 解得 a 6 =0. 2.(2014· 福建高考 ) 等差数列 {a n } 的前 n 项和为 S n , 若 a 1 =2,S 3 =12, 则 a 6 等于　 ( 　　 ) A.8 B.10 C.12 D.14 【 解析 】 选 C. 由题得 , 解得 所以 a 6 =a 1 +5d=12. 3.(2014· 辽宁高考 ) 设等差数列 {a n } 的公差为 d, 若数 列 为递减数列 , 则　 ( 　　 ) A.d<0 B.d >0 C.a 1 d<0 D.a 1 d>0 【 解析 】 选 C. 由数列 为递减数列 , 得 又由指数函数性质得 a 1 a n-1 >a 1 a n . 由等差数列的公差为 d 知 ,a n -a n-1 =d, 所以 a 1 a n-1 >a 1 a n ⇒a 1 a n -a 1 a n-1 <0⇒a 1 (a n -a n-1 )<0⇒a 1 d<0. 4.(2013· 安徽高考 ) 设 S n 为等差数列 {a n } 的前 n 项和 ,S 8 =4a 3 ,a 7 =-2, 则 a 9 = 　 ( 　　 ) A.-6 B.-4 C.-2 D.2 【 解析 】 选 A. 由 S 8 =4a 3 ⇒8a 1 + d=4×(a 1 +2d); 由 a 7 = -2⇒a 1 +6d=-2, 联立解得 a 1 =10,d=-2, 所以 a 9 =a 1 +8d =10-16=-6. 5.(2014· 天津高考 ) 设 {a n } 是首项为 a 1 , 公差为 -1 的等 差数列 ,S n 为其前 n 项和 . 若 S 1 ,S 2 ,S 4 成等比数列 , 则 a 1 的 值为 ____________. 【 解析 】 因为 S 1 ,S 2 ,S 4 成等比数列 , 所以 S 2 2 =S 1 S 4 , 即 ( 2a 1 -1) 2 =a 1 (4a 1 -6) , 解得 a 1 =- . 答案 : - 6.(2014· 安徽高考 ) 数列 {a n } 是等差数列 , 若 a 1 +1,a 3 +3, a 5 +5 构成公比为 q 的等比数列 , 则 q=________. 【 解析 】 设等差数列 {a n } 的公差为 d, 则 (a 3 +3) 2 =(a 1 +1)(a 5 +5), 即 [(a 1 +2d)+3] 2 =(a 1 +1)(a 1 +4d+5), 解得 d=-1, 所以 a 3 +3=a 1 +1,a 5 +5=a 1 +1, 所以 q=1. 答案 : 1 热考题型二 　数列求和 【 考情分析 】 难度 : 中档、稍难 题型 : 以解答题为主 考查方式 : 涉及知识面较广 , 常与函数、不等式、方程、推理证明等知识综合在一起考查 , 其中错位求和、裂项求和是考查重点 【 考题集训 】 1.(2015· 四川高考 ) 设数列 {a n }(n =1,2,3,…) 的前 n 项 和 S n 满足 S n =2a n -a 1 , 且 a 1 ,a 2 +1,a 3 成等差数列 . (1) 求数列 {a n } 的通项公式 . (2) 设数列 的前 n 项和为 T n , 求使得 |T n -1|< 成立的 n 的最小值 . 【 解析 】 (1) 当 n ≥ 2 时 , 有 a n =S n -S n-1 =2a n -a 1 -(2a n-1 -a 1 ), 则 a n =2a n-1 (n≥2), =2(n≥2), 则 {a n } 是以 a 1 为首项 ,2 为公比的等比数列 . 又由题意得 2a 2 +2=a 1 +a 3 ⇒2 · 2a 1 +2=a 1 +4a 1 ⇒a 1 =2, 则 a n =2 n (n∈N * ). (2) 由题意得 (n∈N * ), 由等比数列求和公式得 T n = n=10 时 ,2 10 =1024,n=9 时 ,2 9 =512, 所以 |T n -1|< 成立的 n 的最小值为 10. 2.(2014· 广东高考 ) 设各项均为正数的数列 {a n } 的前 n 项和为 S n , 且 S n 满足 S n 2 -(n 2 +n-3)S n -3(n 2 +n)=0,n∈N * . (1) 求 a 1 的值 . (2) 求数列 {a n } 的通项公式 . (3) 证明 : 对一切正整数 n, 有 【 解析 】 (1) 令 n=1, 则 S 1 =a 1 ,S 1 2 -(1 2 +1-3)S 1 -3(1 2 +1)=0, 即 a 1 2 +a 1 -6=0, 解得 a 1 =2 或 a 1 =-3( 舍去 ). (2)S n 2 -(n 2 + n-3)S n -3(n 2 +n)=0 可以整理为 (S n +3)[S n -(n 2 +n)]=0, 因为数列 {a n } 中 a n >0, 所以 S n ≠-3, 只有 S n =n 2 +n. 当 n≥2 时 ,a n =S n -S n-1 =n 2 +n-(n-1) 2 -(n-1)=2n, 而 a 1 =2, 符合 a n =2n, 所以数列 {a n } 的通项公式为 a n =2n(n∈N * ). (3) 因为 所以 故对一切正整数 n, 有 3.(2014· 江西高考 ) 已知首项都是 1 的两个数列 {a n }, {b n }(b n ≠0,n∈N * ) 满足 a n b n+1 -a n+1 b n +2b n+1 b n =0. (1) 令 c n = , 求数列 {c n } 的通项公式 . (2) 若 b n =3 n-1 , 求数列 {a n } 的前 n 项和 S n . 【 解析 】 (1) 因为 b n ≠ 0, 所以由 a n b n+1 -a n+1 b n +2b n+1 b n =0, 所以 c n+1 -c n =2, 所以 {c n } 是以 c 1 = =1 为首项 ,2 为公差的等差数列 , 所以 c n =1+(n-1)×2=2n-1. (2) 由 b n =3 n-1 知 a n =c n b n =(2n-1)3 n-1 , 于是数列 {a n } 的前 n 项和 S n =1 · 3 0 +3 · 3 1 +5 · 3 2 +…+(2n-1) · 3 n-1 , 3S n =1 · 3 1 +3 · 3 2 +…+(2n-3) · 3 n-1 +(2n-1) · 3 n , 相减得 -2S n =1+2 · (3 1 +3 2 +…+3 n-1 )-(2n-1) · 3 n =-2-(2n-2)3 n , 所以 S n =(n-1)3 n +1. 热考题型三 　不等式及一元二次不等式 【 考情分析 】 难度 : 中档 题型 : 以选择题、填空题为主 考查方式 : 考查利用不等式性质比较大小 , 一元二次不等式的解法 , 常与集合、函数等知识相结合命题 【 考题集训 】 1.(2015· 全国卷 Ⅱ) 已知集合 A={-2,-1,0,1,2}, B={x|(x-1)(x+2)<0}, 则 A∩B= 　 ( 　　 ) A.{-1,0} B.{0,1} C.{-1,0,1} D.{0,1,2} 【 解析 】 选 A. 由已知得 B={x|-2b, 则　 ( 　　 ) A.ac>bc 　 B. C.a 2 >b 2 D.a 3 >b 3 【 解析 】 选 D.y =x 3 在 (- ∞ ,+ ∞ ) 上为增函数 , 所以 a 3 >b 3 . 3.(2014· 山东高考 ) 已知实数 x,y 满足 a x ln(y 2 +1) C.sinx>siny D.x 3 >y 3 【 解析 】 选 D. 由 a x y, 所以 选项 具体分析 结论 A y= 在 ( -∞,0) 上递增 , 在 ( 0,+∞) 上递减 无法 判断 B y=ln( x 2 +1) 在 (-∞,0) 上递减 , 在 ( 0,+∞) 上递增 无法 判断 C y=sinx 为周期函数 无法 判断 D y=x 3 在 R 上为增函数 x 3 >y 3 热考题型四 　基本不等式与线性规划 【 考情分析 】 难度 : 低中档 题型 : 以选择题、填空题为主 考查方式 :1. 利用线性规划 , 考查目标函数的最值和目标函数中参数的取值范围 , 常出现截距型、斜率型、距离型等 2. 与函数单调性结合利用基本不等式求最值 3. 利用基本不等式证明某些不等式成立 【 考题集训 】 1.(2015· 山东高考 ) 已知 x,y 满足约束条件 若 z=ax+y 的最大值为 4, 则 a= 　 ( 　　 ) A.3 　　　　 B.2 　　　　 C.-2 　　　　 D.-3 【 解析 】 选 B. 由约束条件可画可行域如图 , 解得 A(2,0),B(1,1). 若过点 A(2,0) 时取最大值 4, 则 a=2, 验证符合条件 ; 若过点 B(1,1) 时取最大值 4, 则 a=3, 而若 a=3, 则 z=3x+y 最大值为 6( 此时 A(2,0) 是最大值点 ), 不符合题意 .( 也可直接代入排除 ) 2.(2014· 湖北高考 ) 若变量 x,y 满足约束条件 则 2x+y 的最大值是　 ( 　　 ) A.2 B.4 C.7 D.8 【 解析 】 选 C. 满足约束条件 的可行域如图中阴影部分所示 : 目标函数 z=2x+y, 即 y=-2x+z, 显然 , 当直 线经过点 B 时 z 的值最大 , 最大值为 7. 3.(2014· 福建高考 ) 已知圆 C:(x-a) 2 +(y-b) 2 =1, 设平面 区域 Ω: 若圆心 C∈Ω, 且圆 C 与 x 轴相切 , 则 a 2 +b 2 的最大值为　 ( 　　 ) A.5 B.29 C.37 D.49 【 解析 】 选 C. 由圆 C 与 x 轴相切可知 ,b=1. 又圆心 C(a,b ) 在平面区域 Ω( 如图 ) 内 , 故 a∈[ -2,6] . 所以当 a=6,b=1 时 ,a 2 +b 2 取最大值为 37. 热考题型五 　推理与证明 【 考情分析 】 难度 : 中档 , 较难 题型 : 三种题型都有可能出现 考查方式 : 1. 以找规律的形式或与不等式结合考查合情推理 2. 用综合法、分析法、反证法证明等式或不等式成立 3. 与集合、不等式、数列等结合 , 考查数学归纳法的应用 【 考题集训 】 1.(2015· 湖北高考 ) 设 x∈R,[x ] 表示不超过 x 的最大整数 . 若存在实数 t, 使得 [t]=1,[t 2 ]=2,…,[t n ]=n 同时成立 , 则正整数 n 的最大值是　 ( 　　 ) A.3 B.4 C.5 D.6 【 解析 】 选 B. 由 [t]=1 得 1 ≤ t<2, 由 [t 2 ]=2 得 2≤t 2 <3, 由 [t 4 ]=4 得 4≤t 4 <5, 所以 2≤t 2 < , 由 [t 3 ]=3 得 3≤t 3 <4, 所以 6≤t 5 <4 , 由 [t 5 ]=5 得 5≤t 5 <6 与 6≤t 5 <4 矛盾 , 故正整数 n 的最大值为 4. 2.(2015· 山东高考 ) 观察下列各式： 照此规律，当 n∈ N * 时， 【 解析 】 由类比推理可知第 n 个等式右端应该是 4 n-1 . 事 实上，由 及 可知， 即 答案 : 4 n-1 3.(2013· 陕西高考 ) 观察下列等式 : (1+1)=2×1 (2+1)(2+2)=2 2 ×1×3 (3+1)(3+2)(3+3)=2 3 ×1×3×5 …… 照此规律 , 第 n 个等式可为 ________. 【 解析 】 考查对规律的观察、概括能力 , 注意项数 , 开始 值和结束值 . 第 n 个等式可为 :(n+1)(n+2)(n+3)… (n+n ) =2 n ×1×3×5×…×(2n-1) 答案 : (n+1)(n+2)(n+3)… (n+n )=2 n ×1×3×5×…×(2n-1) 4.(2015· 江苏高考 ) 已知集合 X={1,2,3},Y n ={1,2,3,…,n} (n∈N * ), 设 S n ={(a,b)|a 整除 b 或 b 整除 a,a∈X,b∈Y n }, 令 f(n ) 表示集合 S n 所含元素个数 . (1) 写出 f(6) 的值 . (2) 当 n≥6 时 , 写出 f(n ) 的表达式 , 并用数学归纳法证明 . 【 解析 】 (1)f(6)=13. (2) 当 n≥6 时 , 下面用数学归纳法证明 : ① 当 n=6 时 ,f(6)=6+2+ =13, 结论成立 ; ② 假设 n=k(k≥6) 时结论成立 , 那么 n=k+1 时 ,S k+1 在 S k 的 基础上新增加的元素在 ( 1,k+1),(2,k+1),(3,k+1) 中产 生 , 分以下情况讨论 : 1) 若 k+1=6t+1, 则 k=6t, 此时有 f(k+1)=f(k)+1=k+2+ =(k+1)+2+ 结论成立 . 2) 若 k+1=6t+2, 则 k=6t+1, 此时有 f(k+1)=f(k)+2 =k+2+ +2=(k+1)+2+ 结论成立 . 3) 若 k+1=6t+3, 则 k=6t+2, 此时有 f(k+1)=f(k)+2 =k+2+ =(k+1)+2+ 结论成立 . 4) 若 k+1=6t+4, 则 k=6t+3, 此时有 f(k+1)=f(k)+2 =k+2+ =(k+1)+2+ 结论成立 . 5) 若 k+1=6t+5, 则 k=6t+4, 此时有 f(k+1)=f(k)+1 =k+2+ =(k+1)+2+ 结论成立 . 6) 若 k+1=6t, 则 k=6(t-1)+5, 此时有 f(k+1)=f(k)+3 =k+2+ =(k+1)+2+ 结论成立 . 综上所述 , 结论对 n≥6 的自然数 n 均成立 . 热考题型六　 数列、不等式、推理证明综合 【 考情分析 】 难度 : 中高档 题型 : 以解答题为主 考查方式 :1. 与数列结合 , 证明前 n 项和在某个范围内 2. 以数列为载体 , 证明不等式成立 【 考题集训 】 1.(2014· 湖北高考 ) 已知等差数列 {a n } 满足 :a 1 =2, 且 a 1 ,a 2 ,a 5 成等比数列 . (1) 求数列 {a n } 的通项公式 . (2) 记 S n 为数列 {a n } 的前 n 项和 , 是否存在正整数 n, 使得 S n >60n+800? 若存在 , 求 n 的最小值 ; 若不存在 , 说明理由 . 【 解析 】 (1) 设数列 {a n } 的公差为 d, 依题意 ,2,2+d, 2+4d 成等比数列 , 故有 (2+d) 2 =2(2+4d), 化简得 d 2 -4d=0, 解得 d=0 或 d=4. 当 d=0 时 ,a n =2; 当 d=4 时 ,a n =2+(n-1) · 4=4n-2, 从而得数列 {a n } 的通项公式为 a n =2 或 a n =4n-2. (2) 当 a n =2 时 ,S n =2n. 显然 2n<60n+800, 此时不存在正整数 n, 使得 S n >60n+800 成立 . 当 a n =4n-2 时 , 令 2n 2 >60n+800, 即 n 2 -30n-400>0, 解得 n>40 或 n<-10( 舍去 ), 此时存在正整数 n, 使得 S n >60n+800 成立 ,n 的最小值为 41. 综上 , 当 a n =2 时 , 不存在满足题意的 n. 当 a n =4n-2 时 , 存在满足题意的 n, 其最小值为 41. 2.(2013· 北京高考 ) 给定数列 a 1 ,a 2 ,…,a n . 对 i=1,2,…, n-1, 该数列前 i 项的最大值记为 A i , 后 n-i 项 a i+1 ,a i+2 ,…, a n 的最小值记为 B i ,d i =A i -B i . (1) 设数列 {a n } 为 3,4,7,1, 写出 d 1 ,d 2 ,d 3 的值 . (2) 设 a 1 ,a 2 ,…,a n (n≥4) 是公比大于 1 的等比数列 , 且 a 1 >0, 证明 :d 1 ,d 2 ,…,d n-1 是等比数列 . (3) 设 d 1 ,d 2 ,…,d n-1 是公差大于 0 的等差数列 , 且 d 1 >0, 证明 :a 1 ,a 2 ,…,a n-1 是等差数列 . 【 解析 】 (1)d 1 =A 1 -B 1 =3-1=2,d 2 =A 2 -B 2 =4-1=3,d 3 =A 3 -B 3 = 7-1=6. (2) 由 a 1 ,a 2 ,…,a n (n≥4) 是公比大于 1 的等比数列 , 且 a 1 >0, 可得 {a n } 的通项为 a n =a 1 · q n-1 且为单调递增数列 . 于是当 k=2,3,…,n-1 时 , 为定值 . 因此 d 1 ,d 2 ,…,d n-1 构成首项 d 1 =a 1 -a 2 , 公比为 q 的等比数列 . (3) 若 d 1 ,d 2 ,…,d n-1 是公差大于 0 的等差数列 , 则 00 矛盾 . 因而 k≥2, 此时考虑 d k-1 =A k-1 -B k-1 =a k-1 -a k <0, 矛盾 . 因此 ,a n 为数列 {a n } 中的最小项 . 综上 , d k = A k -B k = a k -a n (k =1,2,…,n-1), 于是 a k = d k +a n , 从而 a 1 ,a 2 ,…,a n-1 是等差数列 .