2017-2018学年江西省赣州市十四县（市）高二上学期期中数学试题（文科）（解析版）

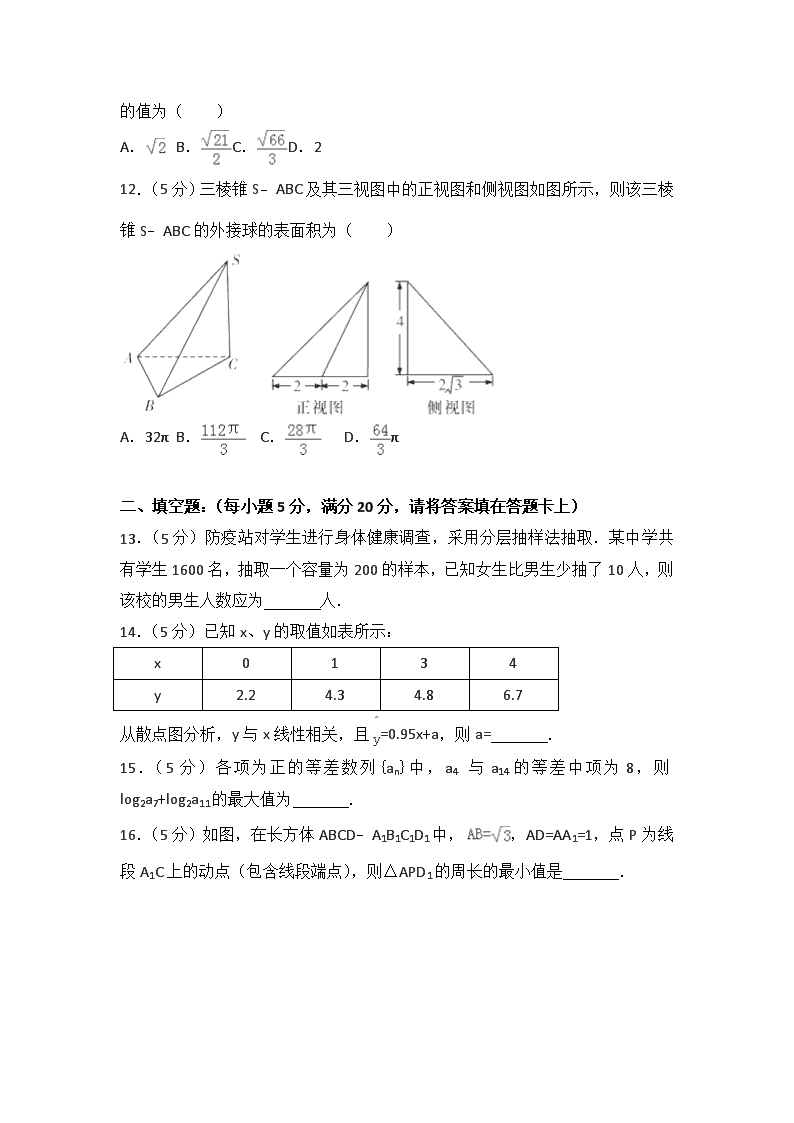
2017-2018学年江西省赣州市十四县（市）高二上学期期中数学试题（文科）（解析版）

‎2017-2018学年江西省赣州市十四县（市）高二（上）期中数学试卷（文科）‎ ‎　‎ 一、选择题：（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．（5分）总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第6个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ ‎（　　）‎ A．07 B．04 C．02 D．08‎ ‎2．（5分）已知直线l过点（0，3），且与直线x﹣y﹣1=0垂直，则l的方程是（　　）‎ A．x+y﹣2=0 B．x﹣y+2=0 C．x+y﹣3=0 D．x﹣y+3=0‎ ‎3．（5分）已知向量，，则在上的投影为（　　）‎ A． B． C．1 D．﹣1‎ ‎4．（5分）圆心为（0，1）且与直线y=﹣2相切的圆的方程为（　　）‎ A．（x﹣1）2+y2=9 B．（x+1）2+y2=9 C．x2+（y﹣1）2=9 D．x2+（y+1）2=9‎ ‎5．（5分）某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从33～48这16个数中取的数是39，则在第1小组1～16中随机抽到的数是（　　）‎ A．5 B．7 C．11 D．13‎ ‎6．（5分）设m，n，l为不重合的直线，α，β，γ是不重合的平面，则下列说法正确的个数是（　　）‎ ‎①若m∥l，n∥l，则m∥n； ②若m⊥l，n⊥l，则m∥n；‎ ‎③若m∥l，m∥α，则l∥α； ④若l∥m，l⊂α，m⊂β，则α∥β；‎ ‎⑤若m⊂α，m∥β，l⊂β，l∥α，则α∥β；⑥若α∥γ，β∥γ，则α∥β A．0 B．1 C．2 D．3‎ ‎7．（5分）程序框图如图所示：如果程序运行的结果S=1320，那么判断框中应填入（　　）‎ A．K＜10 B．K≤10 C．K＜9 D．K≤11‎ ‎8．（5分）已知函数f（x）=Acos（ωx+φ） （A＞0，ω＞0，|φ|＜）的图 象如图所示，若将函数f（x）的图象向右平移个单位，则所得的函数解析式为（　　）‎ A．y=2cos（2x+） B．y=2cos（2x﹣） C． D．‎ ‎9．（5分）正方体ABCD﹣A1B1C1D1中，E是棱BB1中点，G是DD1中点，F是BC上一点且FB=BC，则GB与EF所成的角为（　　）‎ A．30° B．120° C．60° D．90°‎ ‎10．（5分）已知x，y满足，则（x﹣1）2+（y﹣2）2的取值范围是（　　）‎ A．[5，25] B．[1，25] C．[2，29] D．‎ ‎11．（5分）点P（x，y）是直线kx+y+4=0（k＞0）上动点，PA，PB是圆C：x2+y2‎ ‎﹣2y=0的两条切线，A，B是切点，若四边形PABC面积的最小值是2，则k的值为（　　）‎ A． B． C． D．2‎ ‎12．（5分）三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示，则该三棱锥S﹣ABC的外接球的表面积为（　　）‎ A．32π B． C． D．π ‎　‎ 二、填空题：（每小题5分，满分20分，请将答案填在答题卡上）‎ ‎13．（5分）防疫站对学生进行身体健康调查，采用分层抽样法抽取．某中学共有学生1600名，抽取一个容量为200的样本，已知女生比男生少抽了10人，则该校的男生人数应为　 　人．‎ ‎14．（5分）已知x、y的取值如表所示：‎ x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ 从散点图分析，y与x线性相关，且=0.95x+a，则a=　 　．‎ ‎15．（5分）各项为正的等差数列{an}中，a4 与a14的等差中项为8，则log2a7+log2a11的最大值为　 　．‎ ‎16．（5分）如图，在长方体ABCD﹣A1B1C1D1中，，AD=AA1=1，点P为线段A1C上的动点（包含线段端点），则△APD1的周长的最小值是　 　．‎ ‎　‎ 三、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（10分）在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC=（2a﹣c）cosB．‎ ‎（1）求角B的大小；‎ ‎（2）若不等式的解集是（﹣∞，a）∪（c，+∞），求△ABC的周长．‎ ‎18．（12分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB=4，BC=3，AC=5，E为A1C1的中点，F分别为BC上的中点．‎ ‎（1）求证：平面ABE⊥平面B1BCC1；‎ ‎（2）求证：C1F∥平面ABE．‎ ‎19．（12分）“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]‎ ‎），得到如图所示的频率分布直方图，已知第一组有6人．‎ ‎（1）求x；‎ ‎（2）求抽取的x人的年龄的中位数（结果保留整数）；‎ ‎（3）从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人，42人，36人，24人，12人，分别记1～5组，从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛代表相应的成绩，年龄组中1～5组的成绩分别为93，96，97，94，90，职业组中1～5组的成绩分别为93，98，94，95，90．‎ ‎（I）分别求5个年龄组和5个职业组成绩的平均数和方差；‎ ‎（II）以上述数据为依据，评价5个年龄组和5个职业组对“一带一路”的认知程度，并谈谈你的感想．‎ ‎20．（12分）已知函数，函数y=f（x）在（0，+∞）上的零点按从小到大的顺序构成数列{an}（n∈N*）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设bn=，求数列{bn}的前n项和Sn．‎ ‎21．（12分）在四棱锥P﹣ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，M为AD的中点，PA=2AB=4．‎ ‎（1）求证：EM∥平面PAC；‎ ‎（2）取PC中点F，证明：PC⊥平面AEF；‎ ‎（3）求点D到平面ACE的距离．‎ ‎22．（12分）已知圆x2+y2+2ax﹣2ay+2a2﹣4a=0（0＜a≤8）的圆心为C，直线l：y=x+m．‎ ‎（Ⅰ）若m=4，求直线l被圆C所截得弦长的最大值；‎ ‎（Ⅱ）若直线l是圆心C下方的切线，当a∈（0，8]上变化时，求m的取值范围．‎ ‎　‎ ‎2017-2018学年江西省赣州市十四县（市）高二（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．（5分）总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第6个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ ‎（　　）‎ A．07 B．04 C．02 D．08‎ ‎【分析】根据随机数表，依次进行选择即可得到结论．‎ ‎【解答】解：从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字中小于20的编号依次为08，02，14，07，02，01，04，其中第二个和第⑤个都是02，重复．‎ 可知对应的数值为．08，02，14，07，01，04‎ 则第6个个体的编号为04．‎ 故选：B．‎ ‎【点评】本题主要考查简单随机抽样的应用，正确理解随机数法是解决本题的关键，比较基础．‎ ‎　‎ ‎2．（5分）已知直线l过点（0，3），且与直线x﹣y﹣1=0垂直，则l的方程是（　　）‎ A．x+y﹣2=0 B．x﹣y+2=0 C．x+y﹣3=0 D．x﹣y+3=0‎ ‎【分析】设与直线x﹣y﹣1=0垂直的直线l的方程是x+y+‎ m=0，把点（0，3）代入解得m．‎ ‎【解答】解：设与直线x﹣y﹣1=0垂直的直线l的方程是x+y+m=0，‎ 把点（0，3）代入可得：0+3+m=0，解得m=﹣3．‎ ‎∴直线l的方程为：x+y﹣3=0．‎ 故选：C．‎ ‎【点评】本题考查了相互垂直的直线斜率之间的关系，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎3．（5分）已知向量，，则在上的投影为（　　）‎ A． B． C．1 D．﹣1‎ ‎【分析】根据题意，由向量、的坐标可得||以及•的值，又由在上的投影为，计算可得答案．‎ ‎【解答】解：根据题意，向量，，‎ 则||==，•=1×3+2×（﹣4）=﹣5，‎ 则在上的投影为==﹣；‎ 故选：B．‎ ‎【点评】本题考查向量数量积的坐标计算，关键是掌握在上的投影的计算方法．‎ ‎　‎ ‎4．（5分）圆心为（0，1）且与直线y=﹣2相切的圆的方程为（　　）‎ A．（x﹣1）2+y2=9 B．（x+1）2+y2=9 C．x2+（y﹣1）2=9 D．x2+（y+1）2=9‎ ‎【分析】根据题意设圆方程为x2+（y﹣1）2=r2，由圆心到直线的距离得到半径r，代入即可得到所求圆的方程 ‎【解答】解：设圆方程为x2+（y﹣1）2=r2，‎ ‎∵直线y=﹣2与圆相切，‎ ‎∴圆心到直线的距离等于半径r，‎ ‎∴r=3，‎ 故圆的方程为：x2+（y﹣1）2=9，‎ 故选：C．‎ ‎【点评】本题考查了点到直线的距离公式和圆的方程等知识，属于基础题．‎ ‎　‎ ‎5．（5分）某中学采用系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号．已知从33～48这16个数中取的数是39，则在第1小组1～16中随机抽到的数是（　　）‎ A．5 B．7 C．11 D．13‎ ‎【分析】根据系统抽样的定义进行求解即可．‎ ‎【解答】解：样本间隔为800÷50=16，‎ ‎∵在从33～48这16个数中取的数是39，‎ ‎∴从33～48这16个数中取的数是第3个数，‎ ‎∴第1小组1～16中随机抽到的数是39﹣2×16=7，‎ 故选：B．‎ ‎【点评】本题主要考查系统抽样的应用，比较基础．‎ ‎　‎ ‎6．（5分）设m，n，l为不重合的直线，α，β，γ是不重合的平面，则下列说法正确的个数是（　　）‎ ‎①若m∥l，n∥l，则m∥n； ②若m⊥l，n⊥l，则m∥n；‎ ‎③若m∥l，m∥α，则l∥α； ④若l∥m，l⊂α，m⊂β，则α∥β；‎ ‎⑤若m⊂α，m∥β，l⊂β，l∥α，则α∥β；⑥若α∥γ，β∥γ，则α∥β A．0 B．1 C．2 D．3‎ ‎【分析】根据空间线面位置关系的定义，性质和判定定理进行判断．‎ ‎【解答】解：由平行公理可知①正确；‎ 若m，n，l为同一平面内的直线，则②正确，若m，n，l不共面，则m与n可能相交，故②错误；‎ 若l⊂α，则③错误；‎ 若α∩β=n，则当m∥l∥n时，命题④结论不成立，故④错误；‎ 若α∩β=n，则当m∥l∥n时，命题⑤结论不成立，故⑤错误；‎ 由面面平行的传递性可知⑥正确．‎ 故选：C．‎ ‎【点评】本题考查了空间线面位置关系的判断，属于中档题．‎ ‎　‎ ‎7．（5分）程序框图如图所示：如果程序运行的结果S=1320，那么判断框中应填入（　　）‎ A．K＜10 B．K≤10 C．K＜9 D．K≤11‎ ‎【分析】按照程序框图的流程写出前几次循环的结果判断出当k为何值时输出，得到判断框中的条件．‎ ‎【解答】解：经过第一次循环得到s=1×12=12，k=12﹣1=11不输出，即k的值不满足判断框的条件 经过第二次循环得到s=12×11=132，k=11﹣1=10不输出，即k的值不满足判断框的条件 经过第三次循环得到s=132×10=1320，k=10﹣1=9输出，即k的值满足判断框的条件 故判断框中的条件是k＜10‎ 故选：A．‎ ‎【点评】本题考查解决程序框图中的循环结构时，常采用写出前几次循环的结果，找规律，属于基础题．‎ ‎　‎ ‎8．（5分）已知函数f（x）=Acos（ωx+φ） （A＞0，ω＞0，|φ|＜）的图 象如图所示，若将函数f（x）的图象向右平移个单位，则所得的函数解析式为（　　）‎ A．y=2cos（2x+） B．y=2cos（2x﹣） C． D．‎ ‎【分析】由周期求出ω，图象过（，2），求解φ，可得f（x）的解析式，再利用函数y=Asin（ωx+φ）的图象变换规律，可得结论．‎ ‎【解答】解：由函数图象可知A=2，‎ f（x）=2cos（ωx+φ）的部分图象可得==，即T=π．‎ ‎∴ω==2．‎ 再由图象过（，2），即2=2cos（+φ）‎ ‎∴cos（φ）=1．‎ ‎∵，|φ|＜）‎ 求得φ=，‎ ‎∴函数f（x）=2cos（ωx+φ）=2cos（2x）‎ 把将f（x）向右平移个单位：可得y=2cos[2（x）]=2cos（2x﹣）‎ 故选：B．‎ ‎【点评】本题主要考查由函数y=Acos（ωx+φ）的部分图象求解析式，函数y=Acos（ωx+φ）的图象变换规律，属于基础题．‎ ‎　‎ ‎9．（5分）正方体ABCD﹣A1B1C1D1中，E是棱BB1中点，G是DD1中点，F是BC上一点且FB=BC，则GB与EF所成的角为（　　）‎ A．30° B．120° C．60° D．90°‎ ‎【分析】：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出GB与EF所成的角的大小．‎ ‎【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，‎ 设正方体ABCD﹣A1B1C1D1的棱长为2，‎ 则G（0，0，1），B（2，2，0），E（2，2，1），F（，2，0），‎ ‎∴=（2，2，﹣1），=（﹣，0，﹣1），‎ 设GB与EF所成的角为θ，‎ 则cosθ===0，‎ ‎∴θ=90°．‎ ‎∴GB与EF所成的角为90°．‎ 故选：D．‎ ‎【点评】本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．‎ ‎　‎ ‎10．（5分）已知x，y满足，则（x﹣1）2+（y﹣2）2‎ 的取值范围是（　　）‎ A．[5，25] B．[1，25] C．[2，29] D．‎ ‎【分析】由约束条件作出可行域，再由（x﹣1）2+（y﹣2）2的几何意义，即可行域内的动点与定点P（1，2）距离的平方求解得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ ‎（x﹣1）2+（y﹣2）2的几何意义为可行域内的动点与定点P（1，2）距离的平方，‎ 由图可知，（x﹣1）2+（y﹣2）2的最小值为，‎ ‎（x﹣1）2+（y﹣2）2的最小值为．‎ ‎∴（x﹣1）2+（y﹣2）2的取值范围是[2，29]．‎ 故选：C．‎ ‎【点评】本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题．‎ ‎　‎ ‎11．（5分）点P（x，y）是直线kx+y+4=0（k＞0）上动点，PA，PB是圆C：x2+y2﹣2y=0的两条切线，A，B是切点，若四边形PABC面积的最小值是2，则k的值为（　　）‎ A． B． C． D．2‎ ‎【分析】根据切线的性质可知当圆心到P的距离最小时，四边形PABC的面积最小，列方程求出k的值即可．‎ ‎【解答】解：圆C的圆心为C（0，1），半径r=1，‎ 设圆心C到直线kx+y+4=0的最小距离为d，‎ 则四边形PABC面积的最小值2S△PAC=2××1×==2，‎ ‎∴d=，即=，‎ 又k＞0，∴k=2．‎ 故选D．‎ ‎【点评】本题考查了直线与圆的位置关系，属于中档题．‎ ‎　‎ ‎12．（5分）三棱锥S﹣ABC及其三视图中的正视图和侧视图如图所示，则该三棱锥S﹣ABC的外接球的表面积为（　　）‎ A．32π B． C． D．π ‎【分析】由三视图画出几何体的直观图，由三视图判断出SC⊥平面ABC、△ABC的形状，取AC中点F并连BF，由线面垂直的定义和勾股定理求出BC，求出△ABC的外接圆的半径，列出方程求出三棱锥外接球的半径，由球的表面积公式求出答案．‎ ‎【解答】解：由三视图可得：SC⊥平面ABC，且底面△ABC为正三角形，‎ 如图所示，取AC中点F，连BF，则BF⊥AC，‎ 在Rt△BCF中，BF=2，CF=2，BC=4，‎ 在Rt△BCS中，CS=4，所以BS=4．‎ 设球心到平面ABC的距离为d，‎ 因为SC⊥平面ABC，且底面△ABC为正三角形，‎ 所以该三棱锥S﹣ABC的外接球是对应三棱柱的外接球，‎ 则球心到平面ABC的距离是SC的一半，即d=2，‎ 因为△ABC的外接圆的半径为，‎ 所以由勾股定理可得R2=d2+（）2=，‎ 则该三棱锥外接球的半径R=，‎ 所以三棱锥外接球的表面积是4πR2=，‎ 故选：B．‎ ‎【点评】本题考查几何体的三视图，线面垂直的定义，以及几何体外接球问题，由三视图正确还原几何体、以及判断几何体位置关系是解题关键．‎ ‎　‎ 二、填空题：（每小题5分，满分20分，请将答案填在答题卡上）‎ ‎13．（5分）防疫站对学生进行身体健康调查，采用分层抽样法抽取．某中学共有学生1600名，抽取一个容量为200的样本，已知女生比男生少抽了10人，则该校的男生人数应为　840　人．‎ ‎【分析】根据分层抽样的定义建立比例关系即可得到结论．‎ ‎【解答】解：设女生为x，则男生为x+10，‎ ‎∵x+x+10=200，‎ ‎∴2x=190，x=95，‎ 则男生为105人，女生95人，‎ 则该校女生人数为1600×=840，‎ 故答案为：840．‎ ‎【点评】本题主要考查分层抽样的应用，根据条件建立比例关系是解决本题的关键．比较基础．‎ ‎　‎ ‎14．（5分）已知x、y的取值如表所示：‎ x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ 从散点图分析，y与x线性相关，且=0.95x+a，则a=　2.6　．‎ ‎【分析】根据表中的数据可以分别求出变量x，y的算术平均值，而根据回归方程知道直线的斜率为0.95，然后带入求截距的公式即可求出a．‎ ‎【解答】解：根据表中数据得：；‎ 又由回归方程知回归方程的斜率为0.95；‎ ‎∴．‎ 故答案为：2.6．‎ ‎【点评】考查线性相关的概念，回归方程中直线的斜率和截距的计算公式，以及变量的算术平均值的计算．‎ ‎　‎ ‎15．（5分）各项为正的等差数列{an}中，a4 与a14的等差中项为8，则log2a7+log2a11的最大值为　6　．‎ ‎【分析】a4 与a14的等差中项为8，可得a4+a14=2×8=a7+a11，再利用基本不等式的性质可得16≥，再利用对数运算性质即可得出．‎ ‎【解答】解：a4 与a14的等差中项为8，∴a4+a14=2×8=a7+a11，‎ ‎∴16≥，化为：a7a11≤64．当且仅当a7=a11=8取等号．‎ 则log2a7+log2a11=log2（a7a11）≤=6．‎ 故答案为：6．‎ ‎【点评】本题考查了对数运算性质、等差数列的通项公式及其性质、基本不等式的性质，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎16．（5分）如图，在长方体ABCD﹣A1B1C1D1中，，AD=AA1=1，点P为线段A1C上的动点（包含线段端点），则△APD1的周长的最小值是　　．‎ ‎【分析】当AP⊥A1C时，△APD1的周长取最小值，利用棱锥的结构特征结合勾股定理，可得答案．‎ ‎【解答】解：∵在长方体ABCD﹣A1B1C1D1中，，AD=AA1=1，‎ 故AP=PD1，AD1=，‎ 则AP⊥A1C时，△APD1的周长取最小值，‎ 连接AC，在Rt△A1AC中，A1A=1，AC==2，‎ A1C==，‎ 则AP==，‎ 即△APD1的周长的最小值是：，‎ 故答案为：‎ ‎【点评】本题考查的知识点是棱柱的结构特征，点到直线的距离，难度中档．‎ ‎　‎ 三、解答题：（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（10分）在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC=（2a﹣c）cosB．‎ ‎（1）求角B的大小；‎ ‎（2）若不等式的解集是（﹣∞，a）∪（c，+∞），求△ABC的周长．‎ ‎【分析】（1）直接利用已知条件和正弦定理，求出B的值．‎ ‎（2）首先根据a和c是一元二次方程的根，进一步建立方程组，利用余弦定理的公式求出结果．‎ ‎【解答】解析：（1）由bcosC=（2a﹣c）cosB，‎ 得：sinBcosC=（2sinA﹣sinC）cosB…（2分）‎ 即sinBcosC+sinCcosB=2sinAcosB，得 sin（B+C）=2sinAcosB，…（3分）‎ 即sinA=2sinAcosB，得cosB=，…（4分）‎ 又B∈（0，π），于是B= …（5分）‎ ‎（2）依题意a、c是方程的两根，‎ 所以：a+c=，ac=1 …（6分）‎ 由余弦定理得：b2=a2+c2﹣2accosB，‎ ‎=（a+c）2﹣3ac，‎ ‎=6﹣3，‎ ‎=3 …（8分）‎ 所以：b=，…（9分），‎ ‎△ABC的周长为．…（10分）‎ ‎【点评】本题考查的知识要点：三角函数关系式的恒等变换，正弦定理和余弦定理的应用，一元二次方程根与系数的关系的应用．‎ ‎　‎ ‎18．（12分）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB=4，BC=3，AC=5，E为A1C1的中点，F分别为BC上的中点．‎ ‎（1）求证：平面ABE⊥平面B1BCC1；‎ ‎（2）求证：C1F∥平面ABE．‎ ‎【分析】（1）根据AB⊥BB1，AB⊥BC可得AB⊥平面B1BCC1，故而平面ABE⊥平面B1BCC1；‎ ‎（2）BA中点为G，连EG，GF，根据四边形FGEC1是平行四边形得出C1F∥平面EG，故而C1F∥平面ABE．‎ ‎【解答】证明：（1）在△ABC中，∵AB=4，BC=3，AC=5，‎ ‎∴AB2+BC2=AC2，∴AB⊥BC，‎ ‎∵BB1⊥平面ABC，AB⊂平面ABC，‎ ‎∴AB⊥BB1，‎ 又BC⊂平面BB1C1C，BB1⊂平面BB1C1C，BC∩BB1=B，‎ ‎∴AB⊥平面BB1C1C，‎ 又AB⊂平面ABE，‎ ‎∴平面ABE⊥平面BB1C1C；‎ ‎（2）取BA中点为G，连EG，GF，‎ ‎∴FG是△ABC的中位线，‎ ‎∴GF∥AC∥A1C1且，‎ ‎∴四边形FGEC1是平行四边形，‎ ‎∴C1F∥EG，又EG⊂平面ABE，C1F⊄平面ABE，‎ ‎∴C1F∥平面ABE．‎ ‎【点评】本题考查了线面平行，面面垂直的判定，属于中档题．‎ ‎　‎ ‎19．（12分）“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称，某市为了了解人们对“一带一路”的认知程度，对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（90分及以上为认知程度高），现从参赛者中抽取了x人，按年龄分成5组（第一组：[20，25），第二组：[25，30），第三组：[30，35），第四组：[35，40），第五组：[40，45]），得到如图所示的频率分布直方图，已知第一组有6人．‎ ‎（1）求x；‎ ‎（2）求抽取的x人的年龄的中位数（结果保留整数）；‎ ‎（3）从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人，42人，36人，24人，12人，分别记1～5组，从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛代表相应的成绩，年龄组中1～5组的成绩分别为93，96，97，94，90，职业组中1～5组的成绩分别为93，98，94，95，90．‎ ‎（I）分别求5个年龄组和5个职业组成绩的平均数和方差；‎ ‎（II）以上述数据为依据，评价5个年龄组和5个职业组对“一带一路”的认知程度，并谈谈你的感想．‎ ‎【分析】（1）根据频率分布直方图求出第一组频率，由此能求出x．‎ ‎（2）设中位数为a，则0.01×5+0.07×5+（a﹣30）×0.06=0.5，由此能求出中位数．‎ ‎（3）（Ⅰ）利用平均数和方差公式能分别求出5个年龄组和5个职业组成绩的平均数和方差．‎ ‎（Ⅱ）从平均数来看两组的认知程度相同，从方差来看年龄组的认知程度更好．感想：结合本题和实际，符合社会主义核心价值观即可．‎ ‎【解答】（本小题满分12分）‎ 解：（Ⅰ）根据频率分布直方图得第一组频率为0.01×5=0.05，‎ ‎∴，∴x=120． …（2分）‎ ‎（Ⅱ）设中位数为a，则0.01×5+0.07×5+（a﹣30）×0.06=0.5，‎ 解得a=．‎ ‎∴中位数为32． …（5分）‎ ‎（Ⅲ）（i）5个年龄组的平均数为=（93+96+97+94+90）=94，‎ 方差为=[（﹣1）2+22+32+02+（﹣4）2]=6，‎ ‎5个职业组的平均数为=（93+98+94+95+90）=94，‎ 方差为=[（﹣1）2+42+02+12+（﹣4）2]=6.8． …（10分）‎ ‎（ii）评价：从平均数来看两组的认知程度相同，从方差来看年龄组的认知程度更好．‎ 感想：一带一路”是指“丝绸之路经济带”和“21世纪海上丝绸之路”的简称．它将充分依靠中国与有关国家既有的双多边机制，借助既有的、行之有效的区域合作平台．“一带一路”战略目标是要建立一个政治互信、经济融合、文化包容的利益共同体、命运共同体和责任共同体，是包括欧亚大陆在内的世界各国，构建一个互惠互利的利益、命运和责任共同体．‎ ‎（结合本题和实际，符合社会主义核心价值观即可．）…（12分）‎ ‎【点评】本题考查频率分布直方图的应用，考查中位数、平均数、方差的求法及应用，是基础题．‎ ‎　‎ ‎20．（12分）已知函数，函数y=f（x）在（0，+∞）上的零点按从小到大的顺序构成数列{an}（n∈N*）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设bn=，求数列{bn}的前n项和Sn．‎ ‎【分析】（1）利用倍角公式、同角三角函数基本关系式可得f（x）=tanx，利用y=f（x）=0，解出即可得出．‎ ‎（2）bn===，利用裂项求和方法即可得出．‎ ‎【解答】解：（1）==tanx，‎ 由tanx=，解得x=kπ+，解得k∈N．‎ ‎∴an=（n﹣1）π+．‎ ‎（2）bn===，‎ ‎==．‎ ‎【点评】本题考查了倍角公式、同角三角函数基本关系、三角函数求值、裂项求和方法，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎21．（12分）在四棱锥P﹣ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA ‎⊥平面ABCD，E为PD的中点，M为AD的中点，PA=2AB=4．‎ ‎（1）求证：EM∥平面PAC；‎ ‎（2）取PC中点F，证明：PC⊥平面AEF；‎ ‎（3）求点D到平面ACE的距离．‎ ‎【分析】（1）可得EM∥PA，即可证明ME⊄平面PAC，则EM∥平面PAC．‎ ‎（2）取PC中点F，只需证明 PC⊥AF，PC⊥CD即可证明 PC⊥平面AEF．‎ ‎（3）设点D到平面ACE的距离为h，利用，即可得点D到平面ACE的距离．‎ ‎【解答】解：（1）因为E为PD的中点，M为AD的中点，则在△PAD中，EM∥PA，‎ ‎∵PA⊂平面PAC，ME⊄平面PAC，则EM∥平面PAC…（3分）‎ ‎（2）证明：取PC中点F，‎ 在Rt△ABC中，AB=2，∠BAC=60°，则．‎ 而PA=4，则在等腰三角形APC中 PC⊥AF．①…（4分）‎ 又在△PCD中，PE=ED，PF=FC，则EF∥CD 因为PA⊥平面ABCD，CD⊂平面ABCD，则PA⊥CD，…（5分）‎ 又∠ACD=90°，即AC⊥CD，AC∩PA=A，则CD⊥平面PAC，‎ 所以PC⊥CD因此EF⊥PC． ②…（6分）‎ 又EF∩AF=F，由①②知 PC⊥平面AEF…（7分）‎ ‎（3）在Rt△ACD中，，∴…（8分）‎ 又EM∥PA，PA⊥平面ABCD，∴EM⊥平面ABCD，‎ 即EM为三棱锥E﹣ACD的高…（9分）∴…（10分）‎ 在△ACE中，，∴S△ACE=8…（11分）‎ 设点D到平面ACE的距离为h，‎ 则∴，‎ 即点D到平面ACE的距离为．…（12分）‎ ‎【点评】本题考查了线面平行、垂直，点到面的距离，属于中档题．‎ ‎　‎ ‎22．（12分）已知圆x2+y2+2ax﹣2ay+2a2﹣4a=0（0＜a≤8）的圆心为C，直线l：y=x+m．‎ ‎（Ⅰ）若m=4，求直线l被圆C所截得弦长的最大值；‎ ‎（Ⅱ）若直线l是圆心C下方的切线，当a∈（0，8]上变化时，求m的取值范围．‎ ‎【分析】（Ⅰ）求出圆的圆心与半径，求出圆心到直线的距离，利用圆心距半径半弦长满足勾股定理，推出弦长的表达式，然后求解直线l被圆C所截得弦长的最大值；‎ ‎（Ⅱ）利用点到直线的距离等于半径，推出m、a的关系式，结合a的范围，求解m的范围即可．‎ ‎【解答】解：（Ⅰ）圆方程为（x+a）2+（y﹣a）2=4a，‎ 所以圆心C（﹣a，a），半径为r=2‎ 设直线l被圆截得的弦长为AB，圆心C到直线l的距离为d，‎ 当m=4时，，‎ ‎∴‎ 又a∈（0，8]，‎ ‎∴．‎ ‎（Ⅱ）∵，由题意知d=r，‎ ‎∴∵直线l在圆C的下方，‎ ‎∴，‎ ‎∵a∈（0，8]⇒m∈[﹣1，8]‎ ‎【点评】本题考查直线与圆的方程的应用，直线与圆的位置关系的应用，考查转化思想以及计算能力．‎ ‎　‎