- 2021-06-30 发布 |
- 37.5 KB |
- 8页
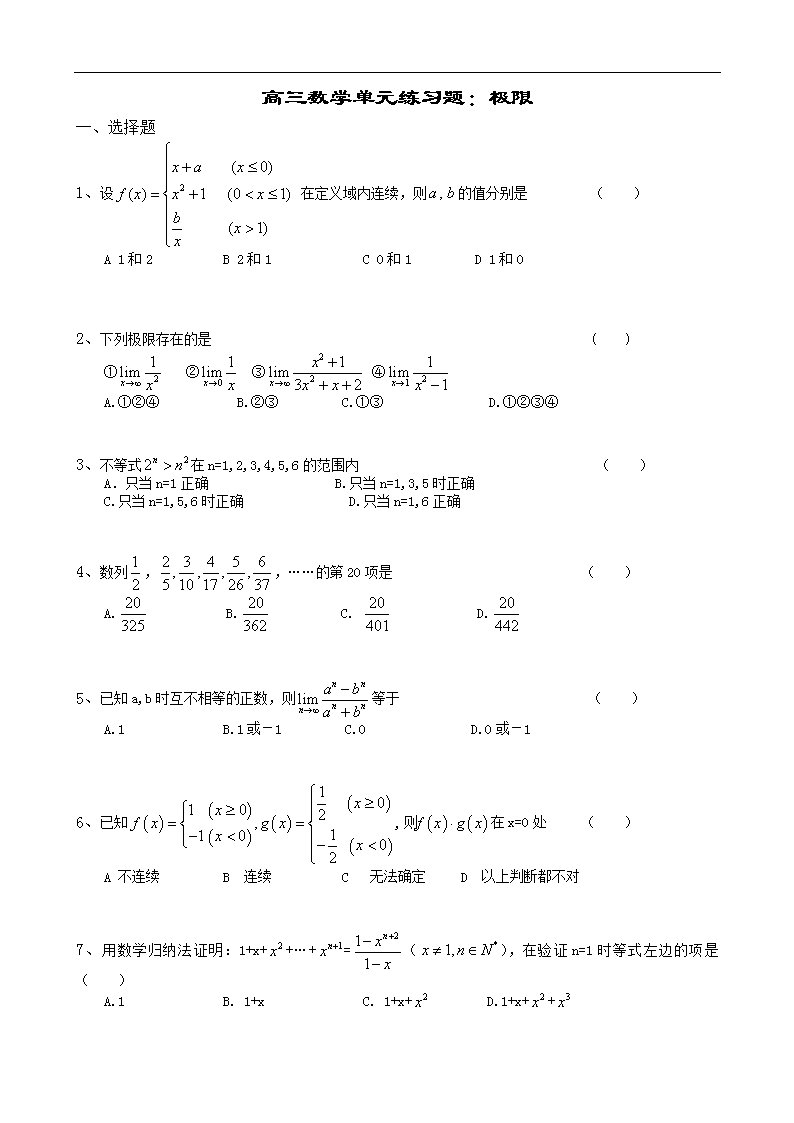

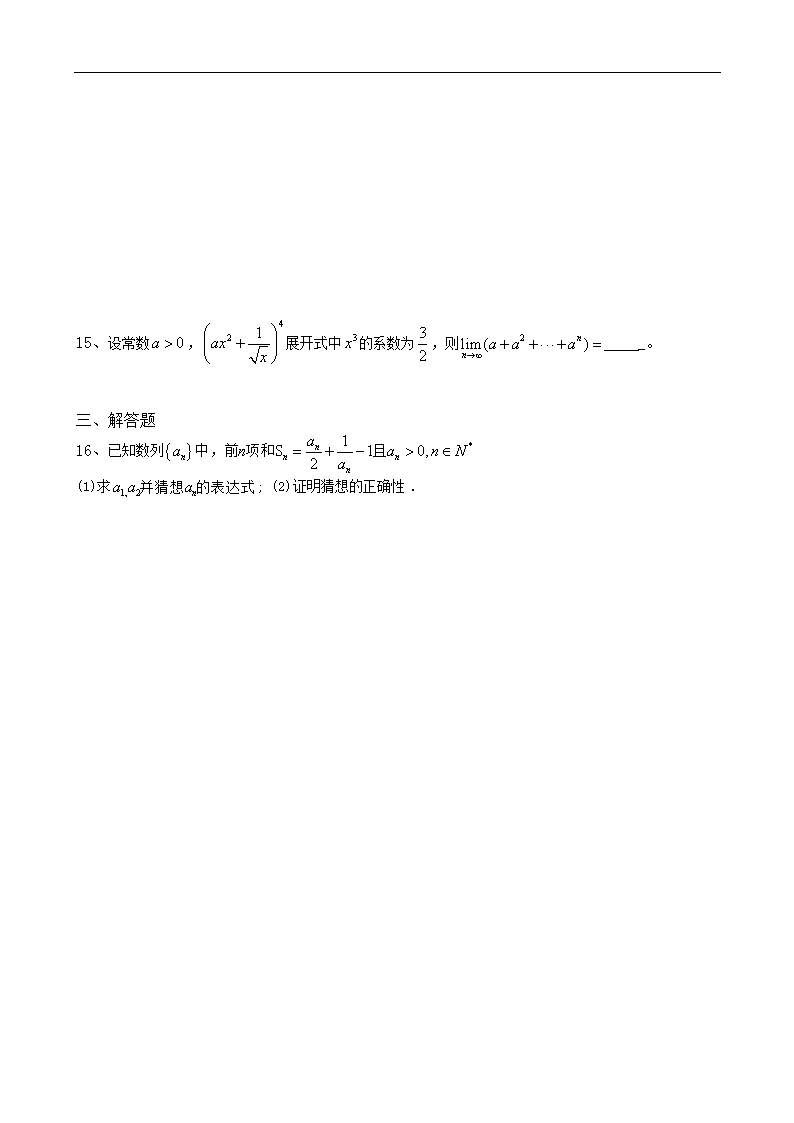
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:单元练习题:极限
高三数学单元练习题:极限 一、选择题 1、设 在定义域内连续,则的值分别是 ( ) A 1和2 B 2和1 C 0和1 D 1和0 2、下列极限存在的是 ( ) ① ② ③ ④ A.①②④ B.②③ C.①③ D.①②③④ 3、不等式在n=1,2,3,4,5,6的范围内 ( ) A.只当n=1正确 B.只当n=1,3,5时正确 C.只当n=1,5,6时正确 D.只当n=1,6正确 4、数列,,……的第20项是 ( ) A. B. C. D. 5、已知a,b时互不相等的正数,则等于 ( ) A.1 B.1或-1 C.0 D.0或-1 6、已知在x=0处 ( ) A 不连续 B 连续 C 无法确定 D 以上判断都不对 7、用数学归纳法证明:1+x++…+=(),在验证n=1时等式左边的项是 ( ) A.1 B. 1+x C. 1+x+ D.1+x++ 8、若点x=1处连续,则f(1)等于 ( ) A B C 0 D 3 9、用数学归纳法证明(n+1)(n+2)(n+3)…..(n+n)=·1·3….(2n-1) (n)时,从n=k到n=k+1时,左边需要增乘的代数式是 ( ) A 2k+1 B C 2k-1 D 10、等于 ( ) A.1 B. C. c D.1或 二、填空题 11、若 。 12、 在则常数k=_______________。 13、_____________。 14、将杨辉三角中的每一个数都换成,就得到一个如下图所示的分数三角形,成为莱布尼茨三角形。从莱布尼茨三角形可看出 ,其中 。 令, 则 。 15、设常数,展开式中的系数为,则 _。 三、解答题 16、已知数列 (1)求; (2)证明猜想的正确性 . 17、求 18、已知,求a 的取值范围. 19、设函数 求一个一次函数使在处都连续。 20、若不等式求正整数m的最大值。 21、已知函数的定义域为R, 且, 求证: 以下是答案 一、选择题 1、A 2、C 3、C 4、C 5、B 6、B 7、C 8、D 9、B 10、D 二、填空题 11、2; 12、3 ; 13、-1; 14、15、r+1,1/2。 15、1 三、解答题 16、解: 同理得, 猜想 (2)证明:n=1时, 假设n=k 时,猜想正确, 即 又 即n=k+1时也成立 17、解 18、解:依题意有: 19、解 要使处都连续,则必须有 且 即同时过两点 即为所求 20、解:设 = = 21、证:的定义域为R 若a=0,则f(x) =1与矛盾 又 综上所述,a>0,b<0查看更多