2020届二轮复习.向量的加法课件（16张）（全国通用）

2020届二轮复习.向量的加法课件（16张）（全国通用）

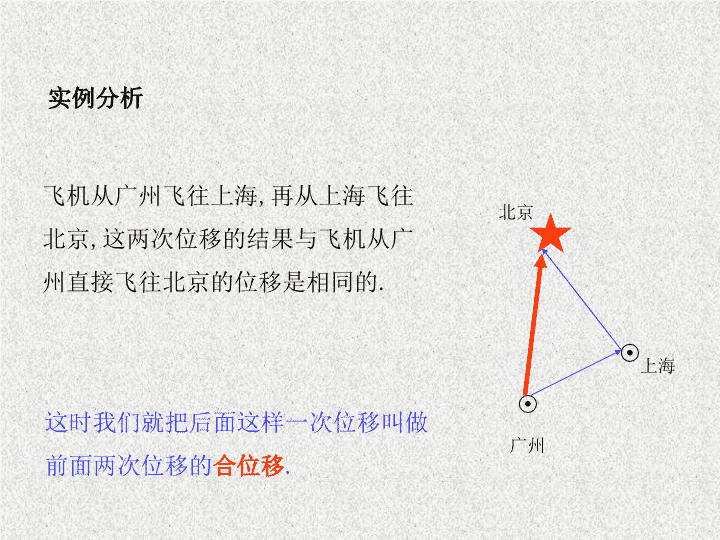
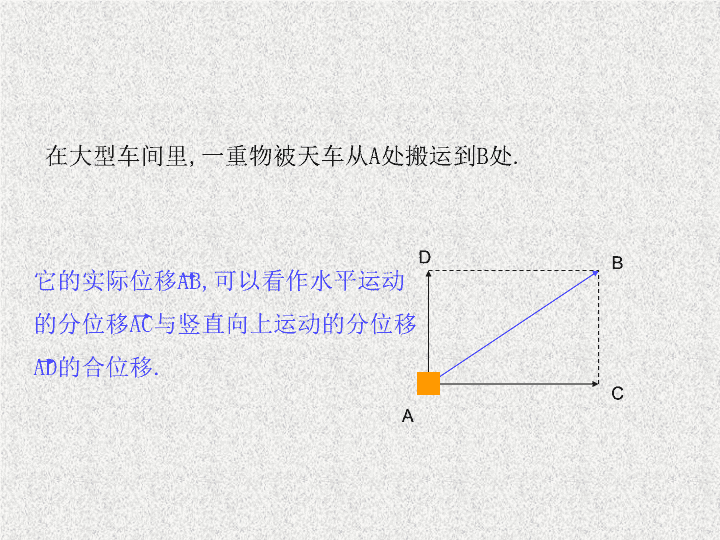
2.1 向量的加法 北京 广州 上海 实例分析 飞机从广州飞往上海 , 再从上海飞往北京 , 这两次位移的结果与飞机从广州直接飞往北京的位移是相同的 . 这时我们就把后面这样一次位移叫做前面两次位移的 合位移 . A B 在大型车间里 , 一重物被天车从 A 处搬运到 B 处 . 它的实际位移 AB, 可以看作水平运动的分位移 AC 与竖直向上运动的分位移 AD 的合位移 . C D 由分位移求合位移 , 称为位移的合成 求两个向量和的运算叫向量的加法。 a b 这种作法叫做 三角形法则 a b A. B a C b 作法 ： [1] 在平面内任取一点 A [2] 作 AB= a , BC= b [3] 则向量 AC 叫 作向量 a 与 b 的和，记作 a ＋ b 。 b a + 这叫做向量加法的 平行四边形法则。 作法： 作 AB= a , AD = b , 以 AB ， AD 为邻边 作平行四边形，则 AC = a + b 。 a b A a B b D C a + b 共线向量求和 a b 方向相同 a b 方向相反 C B A A B C 例１轮船从Ａ港沿东偏北 方向行驶了 40 海里到达 B 处 , 再由 B 处沿正北方向行驶 40 海里到达 C 处 . 求此时轮船与 A 港的相对位置 . 东 北 A B 30 C D 向量的加法满足 ① 交换律： a + b = b + a ② 结合律：（ a + b ) + c = a + ( b + c ) A B C D 例 2 两个力 F 1 和 F 2 同时作用在一个物体上 , 其中 F 1 =40N, 方向向东 ,F 2 =30N, 方向向北 , 求它们的合力 . 东 北 O B θ C Ａ Ｂ F 1 F 2 例 3 在小船过河时 , 小船沿垂直河岸方向行驶的速度为 v 1 =3.46km/h ，河水流动的速度 v 2 =2.0km/h ，试求小船过河实际航行速度的大小和方向 . O B A C 1 试用向量方法证明：对角线互相平分的四边形必是平行四边形 . 证明 与 平行且相等 , 结论得证 . 练习 2 求向量 之和 . 练习