- 2021-06-30 发布 |
- 37.5 KB |
- 4页


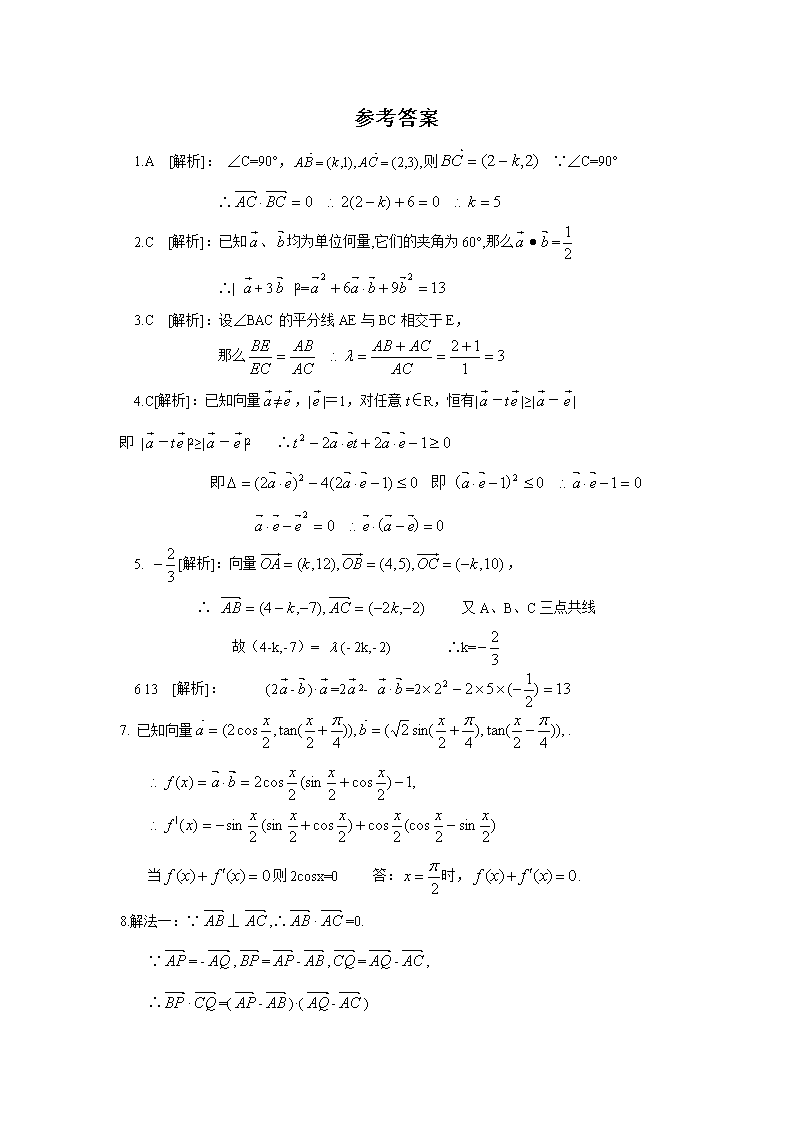
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高三数学复习之30分钟小练习(37)
高三数学复习之30分钟小练习(37) 1. 在△ABC中,∠C=90°,则k的值是 A 5 B -5 C D 2.已知、均为单位何量,它们的夹角为60°,那么| + 3 | = A B C D 4 3. 已知点A(,1),B(0,0)C(,0).设∠BAC的平分线AE与BC相交于E,那么有等于 A 2 B C -3 D - 4. 已知向量≠,||=1,对任意t∈R,恒有|-t|≥|-|,则 A ⊥ B ⊥(-) C ⊥(-) D (+)⊥(-) 5.已知向量,且A、B、C三点共线,则k=___ 6..已知向量与的夹角为120°,且||=2, ||=5,则(2-)·= . 7..已知向量. 是否存在实数若存在,则求出x的值;若不存在,则证明之. 8.如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问 A B C a 与的夹角θ取何值时,·的值最大?并求出这个最大值. 参考答案 1.A [解析]: ∠C=90°,则∵∠C=90° ∴ 2.C [解析]:已知、均为单位何量,它们的夹角为60°,那么= ∴| + 3 |2= 3.C [解析]:设∠BAC的平分线AE与BC相交于E, 那么 4.C[解析]:已知向量≠,||=1,对任意t∈R,恒有|-t|≥|-| 即 |-t|2≥|-|2 ∴ 即 5. [解析]:向量, ∴ 又A、B、C三点共线 故(4-k,- 7)= (- 2k,- 2) ∴k= 6 13 [解析]: (2-)·=22- ·=2 7. 已知向量. 当则2cosx=0 答:时,. 8.解法一:∵⊥,∴·=0. ∵= -,=-,=-, ∴·=(-)·(-) =·-·-·+· = -a2-·+· = -a2-·(-) = -a2+· = -a2+ a2cosθ. 故当cosθ=1,即θ=0 (与方向相同)时, ·最大,最大值为0. 解法二:以直角顶点为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角 x y C Q A B P 坐标系. 设|AB|=c,|AC|=b,则A(0,0),B(0,0),C(0,0). 且|PQ|=2a,|BC|=a. 设点P的坐标为(x,y),则Q(-x, -y), ∴=(x-c, y),=( -x, -y- b). =(-c, b), =(-2x, -2y). ·=( x-c)(-x)+ y(-y- b)= - (x2+y2)+ c x- b y . ∵cosθ=, ∴c x- b y= a2 cosθ. ∴·= -a2+ a2cosθ. 故当cosθ=1,即θ=0 (与方向相同)时, ·最大,最大值为0. 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 Tesoon.com 天 星版权 天·星om 权 天 星 教育网(www.tesoon.com) 版权所有 tesoon 天·星om 权 天·星om 权 Tesoon.com 天 星版权 tesoon tesoon tesoon 天 星查看更多