河南南阳市一中2018届高三第十二次考试数学（理）试题（原卷版）

河南南阳市一中2018届高三第十二次考试数学（理）试题（原卷版）

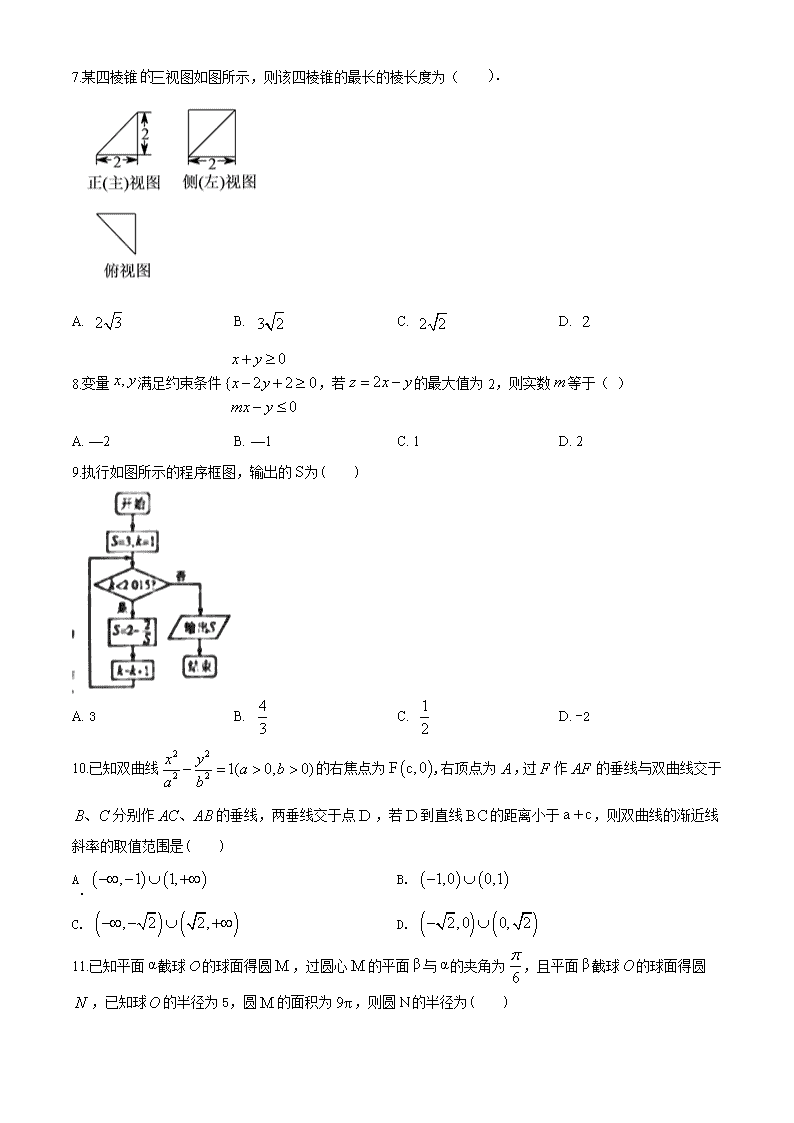
南阳一中 2018 届高三第十二次考试 理数试题 第Ⅰ卷（共 60 分） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1.已知集合 ，则 ( ) A. B. C. D. 2.复数 满足 ,则 ( ) A B. C. D. 3.已知等差数列 ,前 项和为 , ,则 ( ) A. 140 B. 280 C. 168 D. 56 4.已知 的终边上有一点 ,则 ( ) A. B. C. D. 5.设有下面四个命题： ①“若 ，则 与 的夹角为锐角”及它的逆命题均为真命题 ②若 ,则 ③“ ”是“ 或 ”的充分不必要条件 ④命题“ 中，若 ，则 ”的逆命题为真命题 其中正确命题的个数是( ) A. 3 B. 2 C. 1 D. 0 6.设函数 若 ,则实数的 取值范围是( ) A. B. C. D. . { }3A | 0 , 2 44 xxx B xx + = ≥ = −  A B =⌒ ( )2,+∞ ( )4,+∞ )4, +∞ )3,2− z ( ) 2z 1 1 3i i− + = + z = 5 5i− − 5 5i− + 5 5i+ 5 5i− { }na n nS 5 6 28a a+ = 10S = α 4 π− ( )1, 2− sin cosα α− = 6 3 3 − 2 1 3 − 3 3 2 3 3 0a b⋅ > a b : ,2 0xp x R∀ ∈ > 0 0p : ,2 0xx R¬ ∃ ∈ < 1ab ≤ 1a ≤ 1b ≤ ABC A B> sin sinA B> ( ) ( )2 1 2 log , 0, log , 0. x x f x x x >=  − < ( ) ( )f a f a> − a ( ) ( )1,0 0,1− ∪ ( ) ( ), 1 1,−∞ − ∪ +∞ ( ) ( )1,0 1,− ∪ +∞ ( ) ( ), 1 0,1−∞ − ∪ 7.某四棱锥 三视图如图所示，则该四棱锥的最长的棱长度为（ ）． A. B. C. D. 8.变量 满足约束条件 ，若 的最大值为 2，则实数 等于（ ） A. —2 B. —1 C. 1 D. 2 9.执行如图所示的程序框图，输出的 为( ) A. 3 B. C. D. -2 10.已知双曲线 的右焦点为 ,右顶点为 ，过 作 的垂线与双曲线交于 分别作 的垂线，两垂线交于点 ，若 到直线 的距离小于 ，则双曲线的渐近线 斜率的取值范围是( ) A B. C. D. 11.已知平面 截球 的球面得圆 ，过圆心 的平面 与 的夹角为 ，且平面 截球 的球面得圆 ，已知球 的半径为 5，圆 的面积为 ，则圆 的半径为( ) 的 . 2 3 3 2 2 2 2 ,x y 0 { 2 2 0 0 x y x y mx y + ≥ − + ≥ − ≤ 2z x y= − m S 4 3 1 2 2 2 2 2 1( 0, 0)x y a ba b − = > > ( )F c,0 A F AF B C、 AC AB、 D D BC a c+ ( ) ( ), 1 1,−∞ − ∪ +∞ ( ) ( )1,0 0,1− ∪ ( ) ( ), 2 2,−∞ − ∪ +∞ ( ) ( )2,0 0, 2− ∪ α O M M β α 6 π β O N O M 9π N A. 3 B. C. 4 D. 12.已知只有 50 项的数列 满足下列三个条件：① ;② ； ③ .对所有满足上述条件的数列 共有 个不同的值，则 ( ) A. 10 B. 11 C. 6 D. 7 第Ⅱ卷（共 90 分） 二、填空题（每题 5 分，满分 20 分，将答案填在答题纸上） 13.若向区域 内投点，则该点落在由直线 与曲线 围成区域内 的概率为__________． 14. 的展开式中 的系数是__________.(用数字作答) 15.已知 为圆 的直径，点 为直线 上任意一点，则 的最小值 为__________． 16.在锐角 中， 分别为角 所对的边，满足 ,且 的面积 ,则 的取值范围是__________． 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17.已知 为单调递增数列， 为其前 项和， (Ⅰ)求 的通项公式； (Ⅱ)若 为数列 的前 项和，证明： . 18.如图，在直角梯形 中， .直角梯形 通 过直角梯形 以直线 为轴旋转得到，且使得平面 平面 . (Ⅰ)求证：平面 平面 ； (Ⅱ)延长 至点 ，使 为平面 内的动点，若直线 与平面 所成的角为 ， 且 ，求点 到点 的距离的最小值. 13 21 { }na { }1,0,1 1,2, ,50ia i∈ − =  1 2 50 9a a a+ + + = ( ) ( ) ( )2 2 2 1 2 50101 1 1 1 111a a a≤ + + + + + + ≤ { } 2 2 2 1 2 50,na a a a+ + + k k = ( ){ }Ω , | 0 1,0 1x y x y= ≤ ≤ ≤ ≤ y x= y x= ( )( )52x y x y− − 3 3x y AB 2 2: 2 0C x y y+ − = P 1y x= − 2 2| |PA PB+ ABC a,b,c A,B,C ( )a cos 1 cosB b A= + ABC 2S = ( )( )c a b c b a+ − + − { }na nS n 22 n nS a n= + { }na 2 1 1 ,2 n n nn n n ab Ta a + + + =   { }nb n 1 2nT < 1 1AA B B 1 1 1 1 1 190 / / , 1, 2A AB A B AB A B AB AA∠ = ° = = =， 1 1AAC C 1 1AA B B 1AA 1 1AAC C ⊥ 1 1AA B B 1CAB ⊥ 1 1AA B B 1 1B A 1D 1 1 1 1,B A A D E= ABC 1D E 1CAB α 2 5sin 5 α = E B 19.随着移动互联网的快速发展，基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公 司 的经营状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图. (Ⅰ)由折线图得，可用线性回归模型拟合月度市场占有率 与月份代码 之间的关系.求 关于 的线 性回归方程，并预测 公司 2017 年 5 月份（即 时）的市场占有率； (Ⅱ)为进一步扩大市场，公司拟再采购一批单车.现有采购成本分别为 1000 元/辆和 1200 元/辆的 两 款车型可供选择，按规定每辆单车最多使用 4 年，但由于多种原因（如骑行频率等）会导致车辆报废年限 各不形同，考虑到公司运营的经济效益，该公司决定先对两款车型的单车各 100 辆进行科学模拟测试，得 到两款单车使用寿命频数表见上表. 经测算，平均每辆单车每年可以带来收入 500 元，不考虑除采购成本之外的其他成本，假设每辆单车的使 用寿命都是整年，且以频率作为每辆单车使用寿命的概率，如果你是 公司的负责人，以每辆单车产生利 润的期望值为决策依据，你会选择采购哪款车型？ （参考公式：回归直线方程为 ，其中 ） 20.已知抛物线 的焦点为 ，过点 且斜率为 的直线 交曲线 于 两点，交圆 于 两点（ 两点相邻）. (Ⅰ)若 ，当 时，求 的取值范围； M ( )%y x y x M 7x = A B、 M ˆˆ ˆy bx a= + ( )( ) ( ) 1 1 2 2 2 1 1 ˆ,ˆ ˆ n n i i i ii i n n i ii i x x y y x y nxy b a y bx x x x nx = = = = − − − = = = − − − ∑ ∑ ∑ ∑ 2 4C x y=： ( )0,1F F k l C ,A B ( )22 1 1F x y+ − =： ,M N ,A M BF BAλ=  1 2λ 2 3  ∈  ， k (Ⅱ)过 两点分别作曲线 的切线 ，两切线交于点 ，求 与 面积之积的最小值. 21.已知函数 ， ． （Ⅰ）当 时， 恒成立，求 的取值范围； （Ⅱ）当 时，研究函数 的零点个数； （Ⅲ）求证： (参考数据： )． 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修 4-4：坐标系与参数方程 在直角坐标系 中，圆 ，圆 ,以坐标原点 为极点，以 轴正 半轴为极轴，建立极坐标系. (1)求 的极坐标方程； (2)设曲线 （ 为参数且 ）, 与圆 交于 ，求 最大值. 23.已知函数 . (1)求不等式 的解集； (2)若函数 的最小值记为 ，设 ,且有 证明： 的 . ,A B C 1 2,l l P AMP BNP ( ) 31( ) ln( 1), 3f x a x g x x ax= + = − ( ) 1xh x e= − 0x ≥ ( )( )f x h x≤ a 0x < ( ) ( ) ( )F x h x g x= − 101095 3000 1000 2699e< < ln1.1 0.0953≈ xOy ( )2 2 1 1 1C x y− + =： ( )2 2 2 : 3 9C x y− + = O x 1 2C C、 3 cos ,: sin x tC y t α α =  = t 0t ≠ 3C 1 2C C、 A B、 2ABCS ( ) 2 1 1f x x x= − + + ( ) 3f x ≤ ( )y f x= m ,a b R∈ 2 2a b m+ = 2 2 1 4 18 1 1 7a b + ≥+ +