2019届二轮复习三角（含积化和差、和差化积）学案（全国通用）

2019届二轮复习三角（含积化和差、和差化积）学案（全国通用）

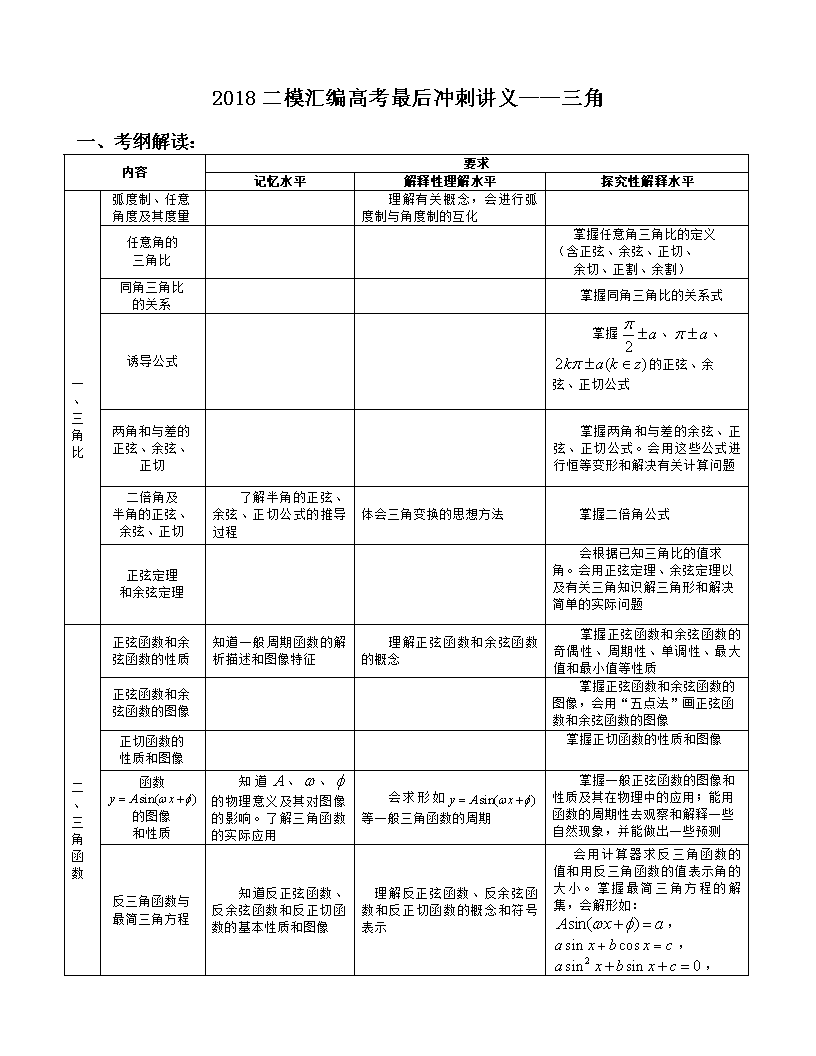
‎2018二模汇编高考最后冲刺讲义——三角 ‎ 一、考纲解读：‎ 内容 要求 记忆水平 解释性理解水平 探究性解释水平 一 ‎、‎ 三角比 弧度制、任意角度及其度量 理解有关概念，会进行弧度制与角度制的互化 任意角的 三角比 掌握任意角三角比的定义（含正弦、余弦、正切、‎ 余切、正割、余割）‎ 同角三角比 的关系 ‎ 掌握同角三角比的关系式 诱导公式 ‎ 掌握、、的正弦、余弦、正切公式 两角和与差的正弦、余弦、正切 ‎ 掌握两角和与差的余弦、正弦、正切公式。会用这些公式进行恒等变形和解决有关计算问题 二倍角及 半角的正弦、余弦、正切 ‎ 了解半角的正弦、余弦、正切公式的推导过程 体会三角变换的思想方法 掌握二倍角公式 正弦定理 和余弦定理 会根据已知三角比的值求角。会用正弦定理、余弦定理以及有关三角知识解三角形和解决简单的实际问题 二 ‎、‎ 三角函数 正弦函数和余弦函数的性质 知道一般周期函数的解析描述和图像特征 理解正弦函数和余弦函数的概念 ‎ 掌握正弦函数和余弦函数的奇偶性、周期性、单调性、最大值和最小值等性质 正弦函数和余弦函数的图像 掌握正弦函数和余弦函数的图像，会用“五点法”画正弦函数和余弦函数的图像 正切函数的 性质和图像 ‎ 掌握正切函数的性质和图像 函数的图像 和性质 知道、、的物理意义及其对图像的影响。了解三角函数的实际应用 ‎ 会求形如等一般三角函数的周期 掌握一般正弦函数的图像和性质及其在物理中的应用；能用函数的周期性去观察和解释一些自然现象，并能做出一些预测 反三角函数与最简三角方程 知道反正弦函数、反余弦函数和反正切函数的基本性质和图像 ‎ 理解反正弦函数、反余弦函数和反正切函数的概念和符号表示 会用计算器求反三角函数的值和用反三角函数的值表示角的大小。掌握最简三角方程的解集，会解形如：‎ ‎，，，‎ 等 简单的三角方程 三、‎ 理 拓展 ‎ 半角的正弦、‎ 余弦、正切 公式的运用 掌握半角的正弦、余弦和正切公式及其基本运用，具有一定的三角变换能力 积化和差与 和差化积 掌握积化和差与和差化积公式的基本运用 二、知识梳理：‎ ‎1、若，则；角的终边越“靠近”轴时，角的正弦、正切的绝对值就较大，角的终边“靠近”轴时，角的余弦、余切的绝对值就较大.‎ ‎【例1】已知，若，则的取值范围是_____________.‎ ‎【答案】‎ ‎【分析】由且，即知其角的终边应“靠近”轴，所以.‎ ‎【例2】方程的解的个数为_____________个.‎ ‎【答案】1‎ ‎【分析】在平面直角坐标系中作出函数与的图像，由函数都是奇函数，而当时恒成立.在时，，所以两函数图像只有一个交点（坐标原点），即方程只有一个解.同样：当时，方程只有唯一解.‎ ‎2、求某个角或比较两角的大小：通常是求该角的某个三角函数值（或比较两个角的三角函数值的大小），然后再定区间、求角（或根据三角函数的单调性比较出两个角的大小）.比如：由未必有；由同样未必有；两个角的三角函数值相等，这两个角未必相等，如；则；或；若，则；若，则.‎ ‎【例1】已知都是第一象限的角，则“”是“”的（　　）‎ A、 充分不必要条件；B、必要不充分条件；C、充要条件；D、既不充分又不必要条件.‎ ‎【答案】D ‎【分析】都是第一象限的角，不能说明此两角在同一单调区间内.如都是第一象限的角，但.选D.‎ ‎【例2】已知，则“”是“”的（　　）‎ A、 充分不必要条件；B、必要不充分条件；C、充要条件；D、既不充分又不必要条件.‎ ‎【答案】C ‎【分析】注意到由，则可以看作是一三角形的两内角.选C.‎ ‎3、已知一个角的某一三角函数值求其它三角函数值或角的大小，一定要根据角的范围来确定；能熟练掌握由的值求的值的操作程序；给（一个角的三角函数）值求（另一个三角函数）值的问题，一般要用“给值”的角表示“求值”的角，再用两角和（差）的三角公式求得.‎ ‎【例1】已知是第二象限的角，且，利用表示_____________‎ ‎【答案】‎ ‎【分析】由是第二象限的角，知，.‎ ‎【例2】已知，求的值.‎ ‎【答案】‎ ‎【分析】由得：，则或.又，所以.由万能公式得，.‎ 知.‎ ‎4、欲求三角函数的周期、最值、单调区间等，应注意运用二倍角正（余）弦公式，半角公式降次即：；引入辅助角（特别注意，经常弄错）使用两角和、差的正弦、余弦公式（合二为一），将所给的三角函数式化为的形式.函数的周期是函数周期的一半.‎ ‎【例1】函数的最小正周期为________；最大值为_________；单调递增区间为_________；在区间上，方程的解集为___________.‎ ‎【分析】由.所以函数的最小正周期为；最大值为2；单调递增区间满足，，即；由，则，‎ 或得或，又由得解集为.注意：辅助角的应用：.其中，且角所在的象限与点所在象限一致.‎ ‎5、当自变量的取值受限制时，求函数的值域，应先确定的取值范围，再利用三角函数的图像或单调性来确定的取值范围，并注意A的正负；千万不能把取值范围的两端点代入表达式求得.‎ ‎【例1】已知函数，求的最大值与最小值.‎ ‎【答案】最大、最小值分别为与.‎ ‎【分析】函数.由，则，，所以函数的最大、最小值分别为与.‎ ‎6、三角形中边角运算时通常利用正弦定理、余弦定理转化为角（或边）处理.有关的齐次式（等式或不等式），可以直接用正弦定理转化为三角式；当知道△ABC三边平方的和差关系，常联想到余弦定理解题；正弦定理应记为（其中R是△ABC外接圆半径.‎ ‎【例1】在△ABC中，分别是对边的长.已知成等比数列，且，求的大小及的值.‎ ‎【答案】‎ ‎【分析】由成等比数列得，则化成，由余弦定理得，.由得，所以=.‎ ‎7、在△ABC中：；，，‎ ‎，等常用的结论须记住.三角形三内角A、B、C成等差数列，‎ 当且仅当.‎ ‎【例1】（1）已知△ABC三边成等差数列，求B的范围；‎ ‎ （2）已知△ABC三边成等比数列，求角B的取值范围.‎ ‎【答案】（1）；（2）‎ ‎【分析】（1）由△ABC的三边成等差数列，则，，消去化得.所以.‎ （2） 同样可以求得.‎ ‎【例2】在△ABC中，若，则△ABC的形状一定是（　　）‎ ‎ A、等腰直角三角形；　　B、直角三角形；　　C、等腰三角形；　　D、等边三角形.‎ ‎【答案】C ‎【分析】在三角形ABC中：，‎ 则.所以△ABC是等腰三角形.‎ ‎【例3】△ABC中，内角A、B、C的对边分别为，已知成等比数列，且.‎ （1） 求的值；（2）设，求的值.‎ ‎【答案】（1）；（2）3‎ ‎【分析】（1）先切化弦：.‎ 由成等比，，所以.‎ 由得，则.‎ ‎（2）注意到，所以，则.又由余弦定理 得：，得，，所以.‎ ‎8、这三者之间的关系虽然没有列入同角三角比的基本关系式，但是它们在求值过程中经常会用到，要能熟练地掌握它们之间的关系式：.求值时能根据角的范围进行正确的取舍.‎ ‎【例1】已知关于的方程有实数根，求实数的取值范围.‎ ‎【答案】或.‎ ‎【分析】由，令，则，其中.则关于的方程在上有解.注意到方程两根之积为1，若有实根必有一根在内，只要△即可，得或.‎ ‎【例2】已知且，则__________.‎ ‎【答案】‎ ‎【分析】此类问题经常出现在各类考试中，而且错误率都比较高.原因是不能根据角所在的象限，对函数值 进行正确的取舍.由平方得，又由知.‎ 则有.，得.‎ 有，所以.‎ ‎9、正（余）弦函数图像的对称轴是平行于轴且过函数图像的最高点或最低点，两相邻对称轴之间的距离是半个周期；正（余）弦函数图像的对称中心是图像与“平衡轴”‎ 的交点，两相邻对称中心之间的距离也是半个周期. 函数的图像没有对称轴，对称中心为.两相邻对称轴之间的距离也是半个周期.‎ ‎【例1】已知函数，且是偶函数，则满足条件的最小正数_________；‎ ‎【答案】‎ ‎【分析】是偶函数，则是它图像的一条对称轴.时，函数取最大（小）值.，.所以满足条件的最小正数.‎ ‎【例2】若函数的图像关于点成中心对称，则_________.‎ ‎【答案】‎ ‎【分析】由的图像关于点成中心对称知，.‎ ‎10、积化和差公式 和差化积公式 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 口诀一：伞加伞，伞在前；伞减伞，鱼在前；‎ 鱼加鱼，两条鱼；鱼减鱼，负两把伞.‎ 口诀二：帅加帅 = 帅哥；帅减帅 = 哥帅；‎ 姑加姑 = 姑姑；哥减哥 = 负嫂嫂.‎ ‎【例1】求证： ‎ ‎【答案】证明 方法一：‎ ‎ = ‎ ‎ =‎ ‎ =‎ 方法二：‎ ‎ = ‎ ‎ =，所以，原等式成立.‎ ‎【例2】已知求 ‎【答案】（1）；（2）‎ ‎【分析】一般地，已知两角的正余弦的和与差，求两角和与差的正余弦，往往采用和差化积或者平方后求和与差。‎ 三、 ‎2018二模汇编：‎ 四、直击高考：‎ ‎1．填空题 ‎1、（2009年理6文10）．函数的最小值是 ‎ ‎【答案】‎ ‎2、（2009年理11）.当，不等式成立，则实数的取值范围是____________.‎ ‎【答案】‎ ‎3、（2009年理12文13）．已知函数.项数为27的等差数列满足,且公差. 若，则当=______时,. ‎ ‎【答案】14‎ ‎4、（2010年理4）．行列式的值为_________.‎ ‎【答案】‎ ‎5、（2010年文3）．行列式的值是 ‎ ‎【答案】0.5‎ ‎6、（2011文4）函数的最大值为 ‎ ‎【答案】‎ ‎7、（2011年理6文8）．在相距2千米的．两点处测量目标，若，‎ ‎ 则．两点之间的距离是 千米。‎ ‎【答案】‎ ‎8、（2011年理8）．函数的最大值为 。‎ ‎【答案】‎ ‎9、（2011年理11文12）在正三角形中，是上的点，，则 ‎ ‎【答案】.‎ ‎10、（2012年理3）函数的值域是 .‎ ‎【答案】 ‎ ‎11、（2012年文3）函数的最小正周期是 .‎ ‎【答案】 ‎ ‎12、（2013年文9）．若，则 ．‎ ‎【答案】-‎ ‎13、（2013年理11）若，则．‎ ‎【答案】‎ 14、 ‎（2014年理1文1）函数的最小正周期是 ．‎ ‎【答案】‎ 15、 ‎（2014年理12）设常数使方程在闭区间上恰有三个解，则 ．‎ ‎【答案】‎ 16、 ‎（2014年文12）方程在区间上的所有的解的和等于 ．‎ ‎【答案】‎ ‎17、（2015年文1）函数的最小正周期为 _________. ‎ 分析：本题是基础题目，主要考查余弦的二倍角公式，属于常考题目。 ‎ 答案：‎ ‎18、（2015年理13文14）已知函数．若存在，，，满足，且 ‎（，），则的最小值 为 ．‎ ‎【答案】‎ ‎【解析】因为，所以，因此要使得满足条件的最小，须取 即 ‎【考点定位】三角函数性质 ‎19、（2016年理7）方程在区间上的解为___________‎ ‎【答案】或 ‎20、（2017年11）设、，且，则的最小值等于 ‎ ‎ ‎【答案】‎ ‎2．选择题 ‎1、（2010年理15文16）.“”是“”成立的 （ ）‎ ‎ 充分不必要条件. 必要不充分条件.‎ ‎ 充分条件. 既不充分也不必要条件 ‎【答案】‎ ‎2、（2010年理18）某人要制作一个三角形，要求它的三条高的长度分别为，则此人能 （ ）‎ ‎ 不能作出这样的三角形 作出一个锐角三角形 ‎ 作出一个直角三角形 作出一个钝角三角形 ‎【答案】‎ ‎3、（2010年文18）若的三个内角满足，则 ( ) 学 ‎ ‎ 一定是锐角三角形. 一定是直角三角形.‎ ‎ 一定是钝角三角形. 可能是锐角三角形，也可能是钝角三角形.‎ ‎ 【答案】 ‎ ‎4、（2011年文 17）若三角方程与的解集分别为和，则（ ）‎ ‎. . . .‎ ‎【答案】‎ ‎5、（2012年理16文17）在中，若，则的形状是（ ）‎ A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定 ‎ 【答案】C ‎6、（2012年理18）设，，在中，正数的个数是（ ）‎ A．25 B．50 C．75 D．100‎ ‎【答案】D ‎7、（2012年文18）若（），则在中，正数的个数是（ ）‎ ‎ A．16 B.72 C.86 D.100‎ ‎【答案】C ‎8、（2015年文理17）已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（ ）‎ ‎ A． B． C． D．‎ ‎【答案】D ‎3．解答题 ‎1、（2009年理20）已知的角、、所对的边分别是、、，设向量，‎ ‎， .‎ ‎（1）若//，求证：为等腰三角形；w.w.w s.5.u.c.o.m ‎ ‎（2）若⊥，边长，角，求的面积 .‎ ‎【答案】证明：（1）‎ 即，其中R是三角形ABC外接圆半径，为等腰三角形 ‎（2）由题意可知 由余弦定理可知， w.w.w s.5.u.c.o.m ‎ ‎2、（2010年文理19）已知，化简：=0‎ ‎【答案】‎ x O y P A ‎3、（2012年文理21）海事救援船对一艘失事船进行定位：以失事船的当前位置为原点，以正北方向为y轴正方向建立平面直角坐标系（以1海里为单位长度），则救援船恰在失事船的正南方向12海里A处，如图. 现假设：①失事船的移动路径可视为抛物线；②定位后救援船即刻沿直线匀速 前往救援；③救援船出发小时后，失事船所在位置的横坐标为.‎ （1） 当时，写出失事船所在位置P的纵坐标. 若此时两船恰好会合，‎ 求救援船速度的大小和方向；‎ ‎（2）问救援船的时速至少是多少海里才能追上失事船？‎ ‎【答案】（1）时，P的横坐标xP=，代入抛物线方程中，得P的纵坐标yP=3. ‎ ‎ 由 AP =，得救援船速度的大小为海里/时. ‎ ‎ 由tan∠OAP=，得∠OAP=arctan，故救援船速度的方向为北偏东arctan弧度. ‎ ‎（2）设救援船的时速为海里，经过小时追上失事船，此时位置为.‎ ‎ 由，整理得. ‎ ‎ 因为，当且仅当=1时等号成立，‎ ‎ 所以，即.因此，救援船的时速至少是25海里才能追上失事船. ‎ ‎4、（2013年文21）已知函数，其中常数．‎ ‎（1）令，判断函数的奇偶性并说明理由；‎ ‎（2）令，将函数的图像向左平移个单位，再往上平移个单位，得到函数的图像．对任意的，求在区间上零点个数的所有可能值．‎ ‎【答案】（1）= ‎ ‎ ‎ ‎ 所以，既不是奇函数也不是偶函数。‎ ‎（2）=‎ ‎ 将的图像向左平移个单位，再向上平移1个单位后得到 ‎ 令 ‎ 因为恰含有10个周期，所以 ‎ 当是零点时，在上零个数为21‎ ‎ 当不是零点时，上恰有 ‎ 两个零点，故在上有20个零点。‎ ‎ 综上，‎ ‎5、（2013年理21）已知函数，其中常数； _X_X_ ‎ ‎（1）若在上单调递增，求的取值范围；‎ ‎（2）令，将函数的图像向左平移个单位，再向上平移1个单位，得到函数的图像，区间（且）满足：在上至少含有30个零点，在所有满足上述条件的中，求的最小值．‎ ‎【答案】(1)因为，根据题意有 ‎ (2) ，‎ ‎ 或， 即的零点相离间隔依次为和，故若在上至少含有30个零点，则的最小值为．‎ ‎6、（2014年理21）如图，某公司要在两地连线上的定点处建造广告牌，其中为顶端，长35米，长80米．设点在同一水平面上，从和看的仰角分别为．‎ ‎（1）设计中是铅垂方向，若要求，问的长至多为多少（结果精确到0.01米）？‎ ‎（2）施工完成后，与铅垂方向有偏差．现在实测得，‎ 求的长（结果精确到0.01米）．‎ ‎[解 ：（1）记．根据已知得，，，‎ ‎ 所以，解得．因此，的长至多约为28.28米．‎ ‎（2）在中，由已知，，，‎ ‎ 由正弦定理得 ，解得．‎ ‎ 在中，有余弦定理得， 解得．‎ ‎ 所以，的长约为26.93米．‎ ‎7、（2015年理20）（本题满分14分）本题共有2小题，第小题满分6分，第小题满分8分 如图，，，三地有直道相通，千米，千米，千米.现甲、乙两警员同时从地出发匀速前往地，经过小时，他们之间的距离为（单位：千米）.甲的路线是，速度为千米/小时，乙的路线是，速度为千米/小时.乙到达地后原地等待.设时乙到达地.‎ ‎（1）求与的值；‎ ‎（2）已知警员的对讲机的有效通话距离是千米.当时，求的表达式，并判断在上得最大值是否超过？说明理由.‎ ‎【答案】（1），（2），不超过.‎ ‎（2）甲到达用时小时；乙到达用时小时，从到总用时小时．‎ 当时，‎ ‎；‎ 当时，.‎ 所以.‎ 因为在上的最大值是，在上的最大值是，所以 在上的最大值是，不超过.‎ ‎【考点定位】余弦定理 ‎8、（2015年文21）（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．‎ 如图，，，三地有直道相通，千米，千米，千米．现甲、乙两警员同时从地出发匀速前往地，经过小时，他们之间的距离为（单位：千米）．甲的路线是，速度为5千米/小时，乙的路线是，速度为8千米/小时．乙到达地后在原地等待．设时，乙到达地．‎ ‎（1）求与的值；‎ ‎（2）已知警员的对讲机的有效通话距离是3千米．当时，求的表达式，并判断在上的最大值是否超过3? 说明理由．‎ 分析：本题是解三角形与函数最值综合的一道应用题，虽然牵扯到分段函数，但并不是很难，主要考察学生的基础知识——余弦定理的应用及二次函数求最值求法.‎ 答案：（1），设此时甲运动到点，则，在中，‎ ‎（2）当时，乙在上，设为点，设此时甲在点，则：，‎ ‎，‎ 当时，乙在点不动，设此时甲在点，则：，‎ 当时，，且的最大值超过了.‎ ‎9、（2017年文18）已知函数，. ‎ ‎（1）求的单调递增区间；‎ ‎（2）设△ABC为锐角三角形，角A所对边，角B所对边，若，求△ABC的面积. ‎ ‎【解析】（1），，单调递增区间为 ‎（2），∴或，‎ 根据锐角三角形，，∴，‎