2017年高考试题——数学理(北京卷)解析版
绝密★本科目考试启用前
2017 年普通高等学校招生全国统一考试
数 学(理)(北京卷)
【试卷点评】
2017 年北京高考数学试卷,试卷内容上体现新课程理念,贴近中学数学教学,坚持对基础知识、基本
技能以及数学思想方法的考查。我先说一说 2017 年总体试卷的难度,2017 年文科也好、理科也好,整个试
卷难度较 2015、2016 年比较平稳,北京高考应该是从 2014 年以前和 2014 年以后,2015、2016 年卷子难度
都比较低,今年延续了前两年,整体难度比较低。今天我说卷子简单在于第 8 题和第 14 题,难度下降了,
相比 2014、2015、2016,整体都下降了。
1.体现新课标理念,实现平稳过渡。试卷紧扣北京考试大纲,新增内容的考查主要是对基本概
念、基本公式、基本运算的考查,难度不大。对传统内容的考查在保持平稳的基础上进行了适度创新,符
合北京一贯的风格。
2.关注通性通法,试卷淡化了特殊的技巧,全面考查通性通法,体现了以知识为载体,以方法
为依托,题目没有偏怪题,以能力考查为目的的命题要求。
3.体现数学应用,联系实际,例如理科第17 题考查了样本型的概率问题,第三问要求不必证明、
直接给出结论(已经连续6年),需注重理解概念的本质原理, 第8 题本着创新题的风格,结合生活中的实
际模型进行考查,像14 年的成绩评定、15 年的汽车燃油问题,都是由生活中的实际模型转化来的,对推动
数学教学中关注身边的数学起到良好的导向。
【试卷解析】
本试卷共 5 页,150 分。考试时长 120 分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试
结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共 40 分)
一、选择题共 8 小题,每小题 5 分,共 40 分。在每小题列出的四个选项中,选出符合题目要求的一项。
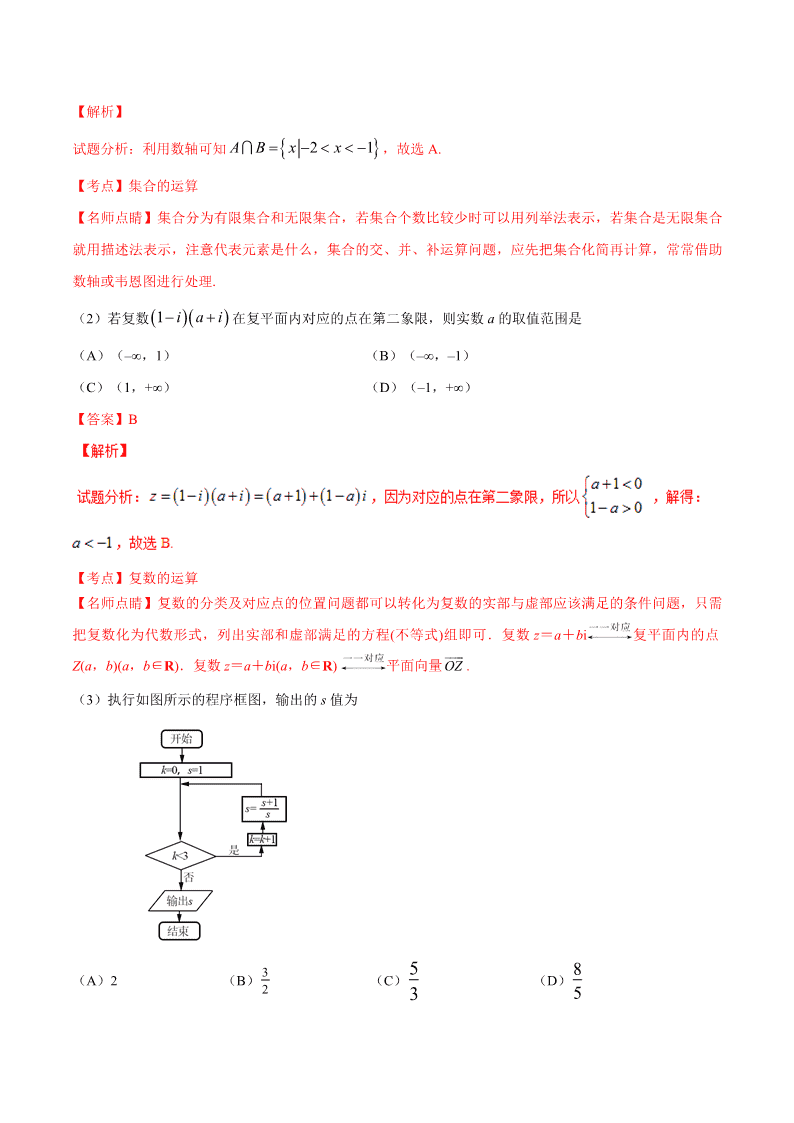
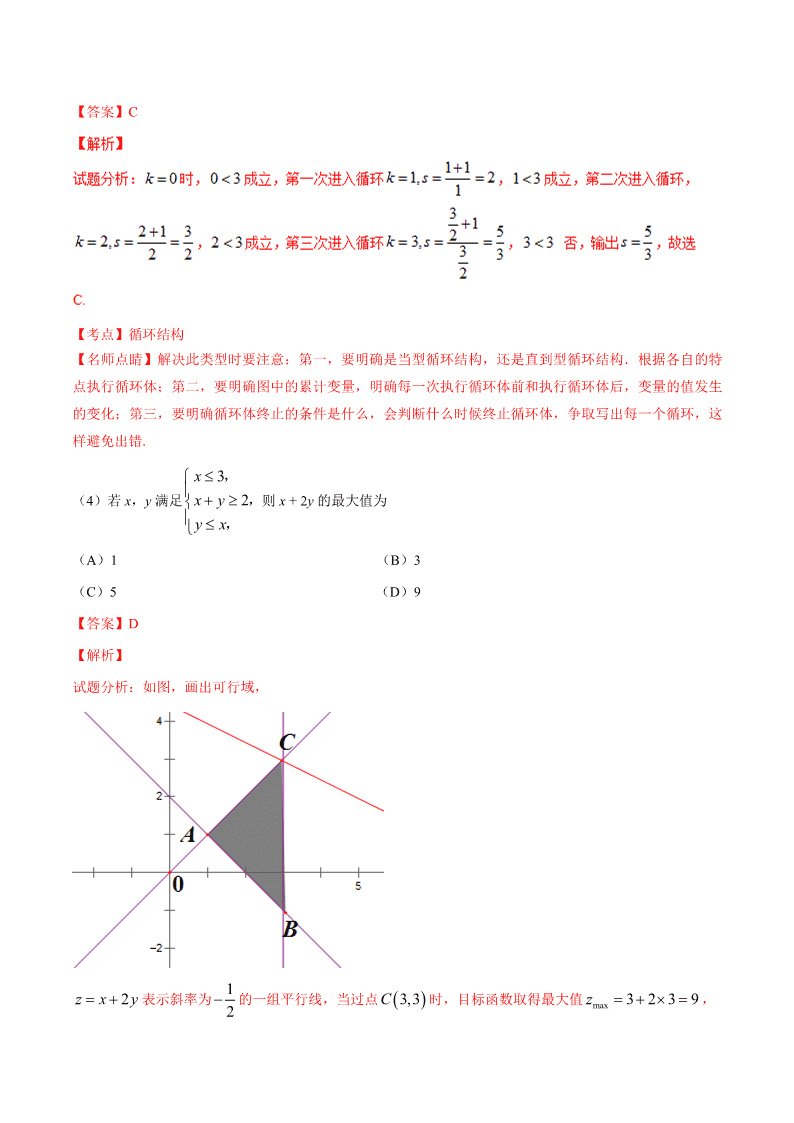
(1)若集合 A={x|–2
3},则 A B=
(A){x|–2 n pn p n p
B PD A 3
2( 1,2, )2M (2,4,0)D 2(3,2, )2MC
MC BDP | | 2 6sin | cos , | 9| || |
MCMC
MC
< > nn
n
MC BDP 2 6
9
(Ⅰ)从服药的 50 名患者中随机选出一人,求此人指标 y 的值小于 60 的概率;
(Ⅱ)从图中 A,B,C,D 四人中随机.选出两人,记 为选出的两人中指标 x 的值大于 1.7 的人数,
求 的分布列和数学期望 E( );
(Ⅲ)试判断这 100 名患者中服药者指标 y 数据的方差与未服药者指标 y 数据的方差的大小.(只需写出结论)
【答案】(Ⅰ)0.3;(Ⅱ)详见解析;(Ⅲ)在这 100 名患者中,服药者指标 数据的方差大于未服药者指
标 数据的方差.
【解析】
(Ⅱ)由图知,A,B,C,D 四人中,指标 的值大于 1.7 的有 2 人:A 和 C.
所以 的所有可能取值为 0,1,2.
.
所以 的分布列为
0 1 2
y
y
x
2 1 1 2
2 2 2 2
2 2 2
4 4 4
C C C C1 2 1( 0) , ( 1) , ( 2)C 6 C 3 C 6P P P
故 的期望 .
(Ⅲ)在这 100 名患者中,服药者指标 数据的方差大于未服药者指标 数据的方差.
【考点】1.古典概型;2.超几何分布;3.方差的定义.
【名师点睛】求分布列的三种方法
1.由统计数据得到离散型随机变量的分布列;
2.由古典概型求出离散型随机变量的分布列;
3.由互斥事件的概率、相互独立事件同时发生的概率及 n 次独立重复试验有 k 次发生的概率求离散型随机
变量的分布列.
(18)(本小题 14 分)
已知抛物线 C:y2=2px 过点 P(1,1).过点(0, )作直线 l 与抛物线 C 交于不同的两点 M,N,过点 M
作 x 轴的垂线分别与直线 OP,ON 交于点 A,B,其中 O 为原点.
(Ⅰ)求抛物线 C 的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A 为线段 BM 的中点.
【答案】(Ⅰ)方程为 ,抛物线 C 的焦点坐标为( ,0),准线方程为 .(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)代入点 求得抛物线的方程,根据方程表示焦点坐标和准线方程;(Ⅱ)设直线 l 的方程
为 ( ),与抛物线方程联立,得到根与系数的关系,直线 ON 的方程为 ,联立求得
点 的坐标 ,证明 .
试题解析:解:(Ⅰ)由抛物线 C: 过点 P(1,1),得 .
所以抛物线 C 的方程为 .
抛物线 C 的焦点坐标为( ,0),准线方程为 .
(Ⅱ)由题意,设直线 l 的方程为 ( ),l 与抛物线 C 的交点为 , .
由 ,得 .
P 1
6
2
3
1
6
1 2 1( ) 0 1 2 16 3 6E
y y
1
2
2y x 1
4
1
4x
P
1
2y kx 0k 2
2
yy xx
B 2 1
1
2
( , )y yx x
1 2
1 1
2
2 0y yy xx
2 2y px 1
2p
2y x
1
4
1
4x
1
2y kx 0k 1 1( , )M x y 2 2( , )N x y
2
1
2y kx
y x
2 24 (4 4) 1 0k x k x
则 , .
因为点 P 的坐标为(1,1),所以直线 OP 的方程为 ,点 A 的坐标为 .
直线 ON 的方程为 ,点 B 的坐标为 .
因为
,
所以 .
故 A 为线段 BM 的中点.
【考点】1.抛物线方程;2.直线与抛物线的位置关系
【名师点睛】本题考查了直线与抛物线的位置关系,考查了转换与化归能力,当看到题目中出现直线与圆
锥曲 线时,不需要特殊技巧,只要联立直线与圆锥曲线的方程,借助根与系数关系,找准题设条件中突显
的或隐含的等量关系,把这种关系“翻译”出来,有时不一定要把结果及时求出来,可能需要整
体代换到后面的计算中去,从而减少计算量.
(19)(本小题 13 分)
已知函数 .
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)求函数 在区间 上的最大值和最小值.
【答案】(Ⅰ) ;(Ⅱ)最大值 1;最小值 .
【解析】
试题分析:(Ⅰ)根据导数的几何意义,求斜率再代入切线方程公式 ;(Ⅱ)设
1 2 2
1 kx x k
1 2 2
1
4x x k
y x 1 1( , )x y
2
2
yy xx 2 1
1
2
( , )y yx x
2 1 1 2 2 1 1 2
1 1
2 2
22y y y y y y x xy xx x
1 2 2 1 1 2
2
1 1( ) ( ) 22 2kx x kx x x x
x
1 2 2 1
2
1(2 2) ( )2k x x x x
x
2 2
2
1 1(2 2) 4 2
kk k k
x
0
2 1
1 1
2
2y yy xx
( ) e cosxf x x x
( )y f x (0, (0))f
( )f x π[0, ]2
1y 2
0 0 0y f f x
,求 ,根据 确定函数 的单调性,根据单调减求函数的最大值 ,
可以知道 恒成立,所以函数 是单调递减函数,根据单调性求最值.
试题解析:(Ⅰ)因为 ,所以 .
又因为 ,所以曲线 在点 处的切线方程为 .
【考点】1.导数的几何意义;2.利用导数求函数的最值.
【名师点睛】这道导数题并不难,比一般意义上的压轴题要简单很多,第二问比较有特点是需要求二阶导
数,因为 不能判断函数的单调性,所以需要再求一次导数,设 ,再求 ,一般这
时就可求得函数 的零点,或是 恒成立,这样就能知道函数 的单调性,根据单调性求最值,
从而判断 的单调性,求得最值.
(20)(本小题 13 分)
设 和 是两个等差数列,记 ,
其中 表示 这 个数中最大的数.
(Ⅰ)若 , ,求 的值,并证明 是等差数列;
(Ⅱ)证明:或者对任意正数 ,存在正整数 ,当 时, ;或者存在正整数 ,使
得 是等差数列.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
h x f x h x 0h x h x 0 0h
0h x f x f x
( ) e cosxf x x x ( ) e (cos sin ) 1, (0) 0xf x x x f
(0) 1f ( )y f x (0, (0))f 1y
f x h x f x h x
h x h x h x
y f x
{ }na { }nb 1 1 2 2max{ , , , }n n nc b a n b a n b a n ( 1,2,3, )n
1 2max{ , , , }sx x x 1 2, , , sx x x s
na n 2 1nb n 1 2 3, ,c c c { }nc
M m n m nc Mn m
1 2, , ,m m mc c c
试 题 分 析 : ( Ⅰ ) 分 别 代 入 求 , 观 察 规 律 , 再 证 明 当 时 ,
, 所 以 关 于 单 调 递 减 . 所 以
,即证明;(Ⅱ)首先求 的通项公式,分
三种情况讨论证明.
(Ⅱ)设数列 和 的公差分别为 ,则
.
所以
①当 时,取正整数 ,则当 时, ,因此 .
此时, 是等差数列.
②当 时,对任意 ,
此时, 是等差数列.
③当 时,
1 2 3, ,c c c 3n
1 1( ) ( ) 2 0k k k kb na b na n k kb na *k N
1 1 2 2 1 1max{ , , , } 1n n nc b a n b a n b a n b a n n nc
1 1 10, 0, 0d d d
{ }na { }nb 1 2,d d
1 2 1 1 1 1 2 1( 1) [ ( 1) ] ( )( 1)k kb na b k d a k d n b a n d nd k
1 1 2 1 2 1
1 1 2 1
( 1)( ),
,n
b a n n d nd d ndc
b a n d nd
当 时,
当 时,
1 0d 2
1
dm d n m 1 2nd d 1 1nc b a n
1 2, , ,m m mc c c
1 0d 1n
1 1 2 1 1 2 1( 1)max{ ,0} ( 1)(max{ ,0} ).nc b a n n d b a n d a
1 2 3, , , , ,nc c c c
1 0d
当 时,有 .
所以
对任意正数 ,取正整数 ,
故当时, .
【考点】1.新定义;2.数列的综合应用;3.推理与证明.
【名师点睛】近年北京卷理科压轴题一直为新信息题,本题考查学生对新定义的理解能力和使用能力,本
题属于偏难问题,反映出学生对于新的信息的的理解和接受能力,本题考查数列的有关知识及归纳法证明
方法,即考查了数列(分段形函数)求值,又考查了归纳法证明和对数据的分析研究,考查了学生的分析
问题能力和逻辑推理能力,本题属于拔高难题,特别是第二两步难度较大,适合选拔优秀学生.
2
1
dn d 1 2nd d
1 1 2 1 1 2
1 1 1 2
( 1)( ) ( )nc b a n n d nd b dn d d a dn n n
1 1 1 2 1 2( ) | |.n d d a d b d
M 1 2 1 1 2 2
1 1
| |max{ , }M b d a d d dm d d
nc Mn