高中数学选修2-2课件数学：2_2_2《反证法》课件（新人教A版选修2-2）

高中数学选修2-2课件数学：2_2_2《反证法》课件（新人教A版选修2-2）

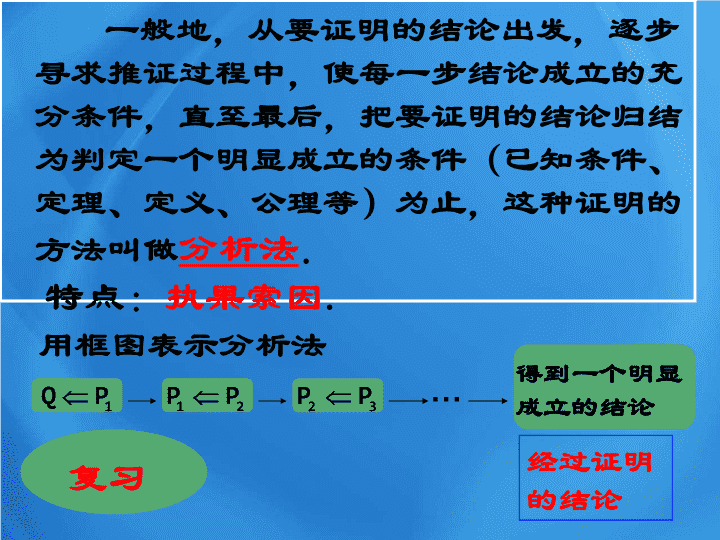
2.2.2 反证法 经过证明的结论 一般地，从要证明的结论出发，逐步寻求推证过程中，使每一步结论成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件（已知条件、定理、定义、公理等）为止，这种证明的方法叫做 分析法 ． 特点： 执果索因 . 用框图表示分析法 得到一个明显成立的结论 … 复习 思考题 : 甲、乙、丙三箱共有小球 384 个 , 先由甲箱取出若干放进乙、丙两箱内 , 所放个数分别为乙、丙箱内原有个数 , 继而由乙箱取出若干个球放进甲、丙两箱内 , 最后由丙箱取出若干个球放进甲、乙两箱内 , 方法同前 . 结果三箱内的小球数恰好相等 . 求甲、乙、丙三箱原有小球数 甲 :208 个 , 乙 :112 个 , 丙 :64 个 思考？ A 、 B 、 C 三个人， A 说 B 撒谎， B 说 C 撒谎， C 说 A 、 B 都撒谎。则 C 必定是在撒谎，为什么？ 分析 : 假设 C 没有撒谎 , 则 C 真 . - - -- - 那么 A 假且 B 假 ; 由 A 假 , 知 B 真 . 这与 B 假矛盾 . 那么 假设 C 没有撒谎不成立 ; 则 C 必定是在撒谎 . 反证法： 假设命题结论的反面成立，经过正确的推理 , 引出矛盾，因此说明假设错误 , 从而证明原命题成立 , 这样的的证明方法叫反证法。 反证法的思维方法： 正难则反 反证法的基本步骤： （ 1 ）假设命题结论不成立，即假设结论的反面成 -- ----- 立； （ 2 ）从这个 假设出发 ，经过推理论证，得出 矛盾 ； （ 3 ）从矛盾判定假设不正确，从而肯定命题的结 - ----- 论正确 归缪矛盾： （ 1 ）与已知条件矛盾； （ 2 ）与已有公理、定理、定义矛盾； （ 3 ）自相矛盾。 应用反证法的情形： (1) 直接证明困难 ; (2) 需分成很多类进行讨论． （ 3) 结论为 “ 至少 ” 、 “ 至多 ” 、 “ 有无穷多个 ” --- 类命题； （ 4 ） 结论为 “ 唯一 ” 类命题； 例 1 ：用反证法证明： 如果 a>b>0 ，那么 例 2 已知 a≠0 ，证明 x 的方程 ax=b 有且只有一个根。 P 例 3 ：证明：圆的两条不全是直径的相交弦不能互相平分 . 已知：在⊙ O 中 , 弦 AB 、 CD 相交于 P ，且 AB 、 CD 不全是直径 求证： AB 、 CD 不能互相平分。 A B C D O 例 4 求证： 是无理数。 作业