数学理卷·2018届河北省石家庄高三教学质量检测（二）（2018

数学理卷·2018届河北省石家庄高三教学质量检测（二）（2018

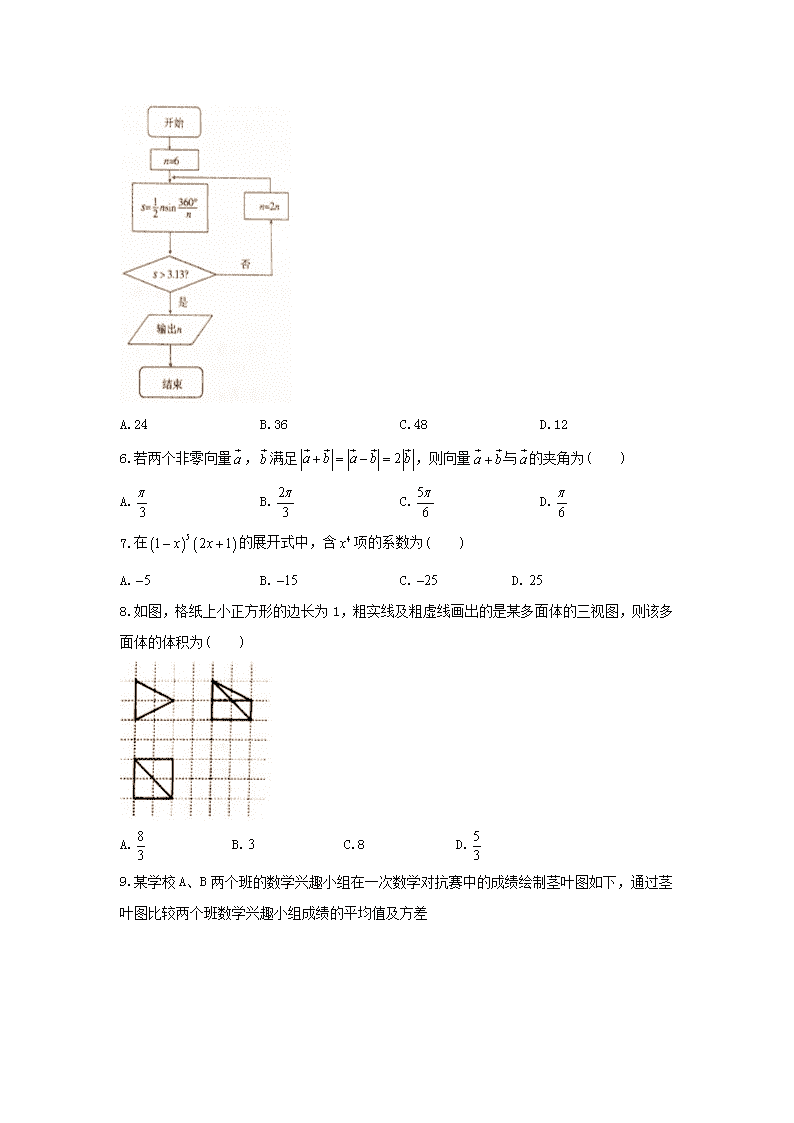
河北省石家庄2018届高三教学质量检测（二）‎ 理科数学 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.设集合，，则下列结论正确的是( )‎ A. B.‎ C. D.‎ ‎2.已知复数满足，若的虚部为，则复数在复平面内对应的点在( )‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎3.在等比数列中，2，，则( )‎ A.28 B.32 C.64 D.14‎ ‎4.设且，则“”是“”的( )‎ A.必要不充分条件 B.充要条件 C.既不充分也不必要条件 D.充分不必要条件 ‎5.我国魏晋期间的伟大的数学家刘徽，是最早提出用逻辑推理的方式来论证数学命题的人，他创立了“割圆术”，得到了著名的“徽率”，即圆周率精确到小数点后两位的近似值，如图就是利用“割圆术”的思想设计的一个程序框图，则输出的值为( )(参考数据：，，)‎ A.24 B.36 C.48 D.12‎ ‎6.若两个非零向量，满足，则向量与的夹角为( )‎ A. B. C. D.‎ ‎7.在的展开式中，含项的系数为( )‎ A. B. C. D.‎ ‎8.如图，格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体的体积为( )‎ A. B. C.8 D.‎ ‎9.某学校A、B两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下，通过茎叶图比较两个班数学兴趣小组成绩的平均值及方差 ‎①A班数学兴趣小组的平均成绩高于B班的平均成绩 ‎②B班数学兴趣小组的平均成绩高于A班的平均成绩 ‎③A班数学兴趣小组成绩的标准差大于B班成绩的标准差 ‎④B班数学兴趣小组成绩的标准差小于A班成绩的标准差 其中正确结论的编号为( )‎ A.①④ B.②③ C.②④ D.①③‎ ‎10.已知函数的部分图象如图所示，已知点，，若将它的图象向右平移个单位长度，得到函数的图象，则函数的图象的一条对称轴方程为( )‎ A. B. C. D.‎ ‎11.倾斜角为的直线经过椭圆右焦点，与椭圆交于、两点，且，则该椭圆的离心率为( )‎ A. B. C. D.‎ ‎12.已知函数是定义在区间上的可导函数，满足且(为函数的导函数)，若且，则下列不等式一定成立的是( )‎ A. B.‎ C. D. ‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.用1，2，3，4，5组成无重复数字的五位数，若用，，，，分别表示五位数的万位、千位、百位、十位、个位，则出现特征的五位数的概率为_____________.‎ ‎14.设变量满足约束条件，则的最大值为_____________.‎ ‎15.已知数列的前项和，如果存在正整数，使得成立，则实数的取值范围是_____________.‎ ‎16.在内切圆圆心为的中，，，，在平面内，过点作动直线，现将沿动直线翻折，使翻折后的点在平面上的射影落在直线上，点在直线上的射影为，则的最小值为_____________.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.已知的内角的对边长分别为，且.‎ ‎(1)求角的大小；‎ ‎(2)设为边上的高，，求的范围.‎ ‎18.随着络的发展，上购物越来越受到人们的喜爱，各大购物站为增加收入，促销策略越来越多样化，促销费用也不断增加，下表是某购物站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据：‎ 月份 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 促销费用 ‎2‎ ‎3‎ ‎6‎ ‎10‎ ‎13‎ ‎21‎ ‎15‎ ‎18‎ 产品销量 ‎1‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ (1) 根据数据可知与具有线性相关关系，请建立关于的回归方程(系数精确到)；‎ (2) 已知6月份该购物站为庆祝成立1周年，特制定奖励制度：以(单位：件)表示日销量，，则每位员工每日奖励100元；，则每位员工每日奖励150元；，则每位员工每日奖励200元.现已知该站6月份日销量服从正态分布，请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位).‎ 参考数据：，，其中，分别为第个月的促销费用和产品销量，.‎ 参考公式：‎ (1) 对于一组数据，，…，，其回归方程的斜率和截距的最小二乘估计分 别为，.‎ (2) 若随机变量服从正态分布，则，.‎ ‎19.如图，三棱柱中，侧面为的菱形，.‎ ‎(1)证明：平面平面.‎ ‎(2)若，直线与平面所成的角为，求直线与平面所成角的正弦值.‎ ‎20.已知圆的圆心在抛物线上，圆过原点且与抛物线的准线相切.‎ ‎(1)求该抛物线的方程；‎ ‎(2)过抛物线焦点的直线交抛物线于两点，分别在点处作抛物线的两条切线交于点，求三角形面积的最小值及此时直线的方程.‎ ‎21.已知函数.‎ ‎(1)讨论函数的单调性；‎ ‎(2)若函数存在极大值，且极大值为1，证明：.‎ ‎22.在直角坐标系中，曲线的参数方程为(其中为参数)，曲线.以原点为极点，轴的正半轴为极轴建立极坐标系.‎ ‎(1)求曲线、的极坐标方程；‎ ‎(2)射线与曲线、分别交于点(且均异于原点)当时，求的最小值.‎ ‎23.已知函数.‎ ‎(1)当时，求的解集；‎ ‎(2)若，当，且时，，求实数的取值范围.‎ 石家庄市2017-2018学年高中毕业班第二次质量检测试题 理科数学答案 一、选择题 ‎1-5BABCC 6-10DBAAD 11‎‎-12AC 二、填空题 ‎13． 14． 3‎ ‎15． 16. ‎ 三、解答题 ‎17.解：（1）在△ABC中 ‎（2）‎ ‎18（1）由题可知， ‎ 将数据代入得 ‎ ‎ 所以关于的回归方程 ‎ ‎（2）由题6月份日销量服从正态分布，则 日销量在的概率为， ‎ 日销量在的概率为， ‎ 日销量的概率为， ‎ 所以每位员工当月的奖励金额总数为 元. ‎ ‎19.证明：（1）连接交于，连接 侧面为菱形， ‎ ‎， 为的中点， ‎ 又，平面 平面 平面平面. ‎ ‎（2）由，，， 平面，平面 从而，，两两互相垂直，以为坐标原点，的方向为轴正方向，建立如图所示空间直角坐标系 直线与平面所成的角为，‎ 设，则，又，△是边长为2的等边三角形 ‎ ‎，‎ 设是平面的法向量，则即 令则 ‎ 设直线与平面所成的角为 则 直线与平面所成角的正弦值为. ‎ ‎20.解：（1）由已知可得圆心，半径，焦点，准线 因为圆C与抛物线F的准线相切，所以， ‎ 且圆C过焦点F，‎ 又因为圆C过原点，所以圆心C必在线段OF的垂直平分线上，‎ 即 ‎ 所以，即，抛物线F的方程为 ‎ ‎（2）易得焦点，直线L的斜率必存在，设为k，即直线方程为 设 得，， ‎ 对求导得，即 直线AP的方程为，即，‎ 同理直线BP方程为 设，‎ 联立AP与BP直线方程解得，即 ‎ 所以，点P到直线AB的距离 ‎ 所以三角形PAB面积，当仅当时取等号 综上：三角形PAB面积最小值为4，此时直线L的方程为. ‎ ‎21．解:‎ ‎（Ⅰ）由题意，‎ ① 当时，，函数在上单调递增；‎ ② 当时，函数单调递增，，故当时，，当时，，所以函数在上单调递减，函数在上单调递增； ‎ ③ 当时，函数单调递减，，故当时，，当时，，所以函数在上单调递增，函数在上单调递减．‎ ‎（Ⅱ）由（Ⅰ）可知若函数存在极大值，则，且，解得， 故此时，‎ 要证，只须证，及证即可，‎ 设，．‎ ‎，令 ‎，所以函数单调递增，‎ 又，，‎ 故在上存在唯一零点，即．‎ 所以当，， 当时，，所以函数在上单调递减，函数在上单调递增，‎ 故，‎ 所以只须证即可，‎ 由，得，‎ 所以，又，所以只要即可，‎ 当时，‎ 所以与矛盾，‎ 故，得证．‎ ‎（另证）‎ 当时，‎ 所以与矛盾；‎ 当时，‎ 所以与矛盾；‎ 当时，‎ 得，故 成立，‎ 得，所以，即．‎ ‎22.解：（1）曲线的普通方程为，的极坐标方程为 的极坐标方程为 ‎（2）联立与的极坐标方程得，‎ 联立与的极坐标方程得，‎ 则= =‎ ‎= ‎ ‎（当且仅当时取等号）.‎ 所以的最小值为 ‎23.‎ 解：当时，‎ 当时，无解；‎ 当时，的解为；‎ 当时，无解；‎ 综上所述，的解集为 当时，‎ 所以可化为 又的最大值必为、之一 ‎ …………………9分 即即 又所以所以取值范围为