数学文卷·2017届辽宁省盘锦市辽河油田第二高级中学高三上学期期末考试（2017

数学文卷·2017届辽宁省盘锦市辽河油田第二高级中学高三上学期期末考试（2017

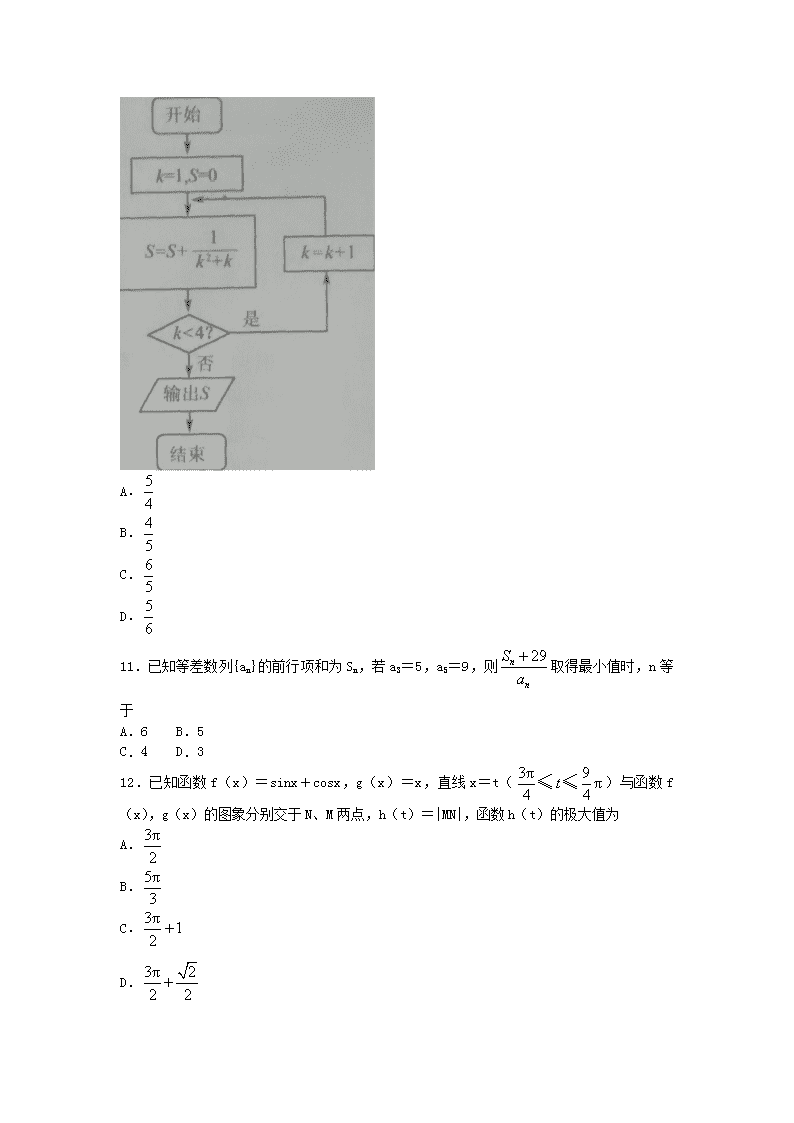
文科数学试题 第Ⅰ卷 一、选择题：‎ ‎1．已知集合A＝{x|x＜0或x＞2}，B＝{x|－1＜x＜1），则等于 A．{x|－1＜x＜1） B．{x|x＜0或x＞2}‎ C．{x|x≤－1或x＞2} D．{x|x≤－1或x≥1}‎ ‎2．如果复数（其中i为虚数单位，b为实数）为纯虚数，那么b＝‎ A．1 B．2 C．4 D．－4‎ ‎3．已知a＝（1，k），b＝（k，4），若a与b反向，则k的值为 A．－2 B．0 C．2 D．±2‎ ‎4．直线y＝2x－1被圆x2＋y2＝1截得的弦长等于 A．‎ B．‎ C．‎ D．2‎ ‎5．命题p：，log2x≥1，则 A．p是真命题，：，log2x0＜1‎ B．p是假命题，：，log2x＜1‎ C．p是假命题，：，log2x0＜1‎ D．p是真命题，：，log2x＜1‎ ‎6．某三棱柱的三视图如图所示，则该三棱柱的表面积是 A．‎ B．‎ C．‎ D．‎ ‎7．如图，某几何图形由半径均为1的两相切圆，以及他们的外公切线围成，现从该图形中任取一点，则该点取自阴影部分的概率为 A．‎ B．‎ C．‎ D．‎ ‎8．设m，n是两条不同的直线，α，β是两个不同的平面，以下判断正确的是 A．若m⊥β，n⊥β，n⊥α，则m⊥α B．若m⊥n，n⊥β，β⊥α，则m⊥α C．若m⊥n，n∥α，则m⊥α D．若m∥β，β∥α，则m⊥α ‎9．设a＝log32，b＝ln2，，则 A．b＞a＞c B．c＞6＞a C．b＞c＞a D．c＞a＞b ‎10．如果执行如图的框图，则输出的数S＝‎ A．‎ B．‎ C．‎ D．‎ ‎11．已知等差数列{an}的前行项和为Sn，若a3＝5，a5＝9，则取得最小值时，n等于 A．6 B．5‎ C．4 D．3‎ ‎12．已知函数f（x）＝sinx＋cosx，g（x）＝x，直线x＝t（）与函数f（x），g（x）的图象分别交于N、M两点，h（t）＝|MN|，函数h（t）的极大值为 A．‎ B．‎ C．‎ D．‎ 第Ⅱ卷 二、填空题：‎ ‎13．双曲线（a＞0，b＞0）地 一条渐近线方程y＝x，则其离心率为________．‎ ‎14．已知经过函数f（x）＝bx＋ex图象上点P（1，f（1））处的切线与直线3x－y平行，则b＝________．‎ ‎15．已知函数，在△ABC中，角A、B、C的对边分别是a、b、c且满足，则f（A）的取值范围是________．‎ ‎16．已知抛物线C：y2＝2px（p＞0）的准线为l，过M（1，0）且斜率为的直线与l相交于点Q，与C的一个交点为B，若M为AB的中点，则p＝________．‎ 三、解答题：‎ ‎17． Sn是数列{an}的前n项和．数列{an}满足an＋1－2an＝0，且S5＝62．‎ ‎（Ⅰ）求数列{an}的通项公式；‎ ‎（Ⅱ）若bn＝11－2log2an，求b1＋b2＋…＋bn．‎ ‎18．某市高三在期中考试后把全市数学成绩按照大于等于120分为“优秀”，120分以下为“待转优”进行统计分析．其中市一中“励志班”和“普通班"的成绩统计列联表如下：‎ 优秀 待转优 总计 励志班 ‎11‎ ‎44‎ ‎55‎ 普通班 ‎20‎ ‎30‎ ‎50‎ 合计 ‎30‎ ‎75‎ ‎105‎ ‎（Ⅰ）根据列联表的数据，计算k的值并判断能有多大把握认为“成绩与班级有关”；‎ ‎（Ⅱ）若按下面的方法从励志班优秀的学生中抽取一人：把励志班优秀的11名学生从2到12进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号．试求抽到6号或10号的概率．‎ 附：‎ P（K2≥k0）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎19．如图，在三棱柱ABC－A1B1C1中，AA1⊥底面ABC，AD⊥平面A1BC，其垂足D落在A1B上．‎ ‎（Ⅰ）求证：BC⊥A1B；‎ ‎（Ⅱ）若，AB＝BC＝2，P为AC的中点，求三棱锥A1－PBC的体积．‎ ‎20．已知函数．‎ ‎（Ⅰ）若a＞0，证明：f（x）在定义域内是增函数；‎ ‎（Ⅱ）若f（x）在上的最小值为，求a的值．‎ ‎21．已知椭圆E：的焦点在x轴上，抛物线C：与椭圆E交于A，B两点，直线AB过抛物线的焦点．‎ ‎（Ⅰ）求椭圆E的方程和离心率e的值；‎ ‎（Ⅱ）已知过点H（2，0）的直线l与抛物线C交于M、N两点，又过M、N作抛物线C的切线l1，l2。，使得l1⊥l2，问这样的直线l是否存在？若存在，求直线l的方程；若不存在，说明理由．‎ ‎22．选修4－4：坐标系与参数方程 已知在平面直角坐标系中，曲线C的方程是x2＋y2－2y＝0，以O为极点，x轴正半轴为极轴，取相同的长度单位建立极坐标系，直线l的参数方程是（t为参数）．‎ ‎（Ⅰ）将曲线C的直角坐标方程化为极坐标方程；‎ ‎（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求|MN|的取值范围．‎ ‎23．选修4－5：不等式选讲 已知f（x）＝|x＋2|＋|x－1|．‎ ‎（Ⅰ）求不等式f（x）＞5的解集；‎ ‎（Ⅱ）若f（x）≥a2－2a恒成立，求实数a的取值范围．‎ 文科数学·参考答案、提示及评分细则 ‎1．C ‎2．A ‎3．A ‎4．A ‎5．A ‎6．B ‎7．D ‎8．A ‎9．B ‎10．B ‎11．A ‎12．C ‎13．‎ ‎14．3－e ‎15．‎ ‎16．2‎ ‎17．解：（Ⅰ）∵an＋1－2an＝0，即an＋1＝2an，∴数列{an}是以2为公比的等比数列．‎ ‎，a1＝2．‎ ‎∴数列{an}的通项公式an＝2n．‎ ‎（Ⅱ）∵an＝2n，∴bn＝11－2n，‎ ‎∴b1＝9，bn＋1－bn＝－2，‎ ‎∴{bn}是公差为－2的等差数列．‎ ‎∴‎ ‎18．解：（Ⅰ）根据列联表中的数据，得到 因此有97.5％的把握认为“成绩与班级有关系”．‎ ‎（Ⅱ）设“抽到6号或10号”为事件A，先后两次抛掷一枚均匀的骰子，出现的点数为（x，y），则所有的基本事件有（1，1），（1，2），（1，3），…，（6，6），共36个．‎ 事件A包含的基本事件有（1，5），（2，4），（3，3），（4，2），（5，1），（4，6），（5，5），（6，4），共8个，‎ ‎∴抽到6号或10号的概率为．‎ ‎19．解：（Ⅰ）∵三棱柱ABC－A1B1C1中A1A⊥平面ABC，又，∴A1A⊥BC ‎∵AD⊥平面A1BC，且，∴AD⊥BC．‎ 又，，A1A∩AD＝A，‎ ‎∴BC⊥平面A1AB，‎ 又，∴BC⊥A1B．‎ ‎（Ⅱ）在三棱柱ABC－A1B1C1中AA1⊥底面ABC，∴A1A⊥AB．∵AD⊥平面A1BC，其垂足D落在A1B上，∴AD⊥A1B．‎ 在Rt△ABD中，，AB＝BC＝2，∴，∠ABD＝60°，在Rt△ABA1中，．‎ 由（Ⅰ）知BC⊥平面A1AB，，从而BC⊥AB，‎ ‎．‎ ‎∵P为AC的中点，∴，‎ ‎∴．‎ ‎20．解：（Ⅰ）由题意知f（x）的定义域为（0，＋∞），‎ ‎．‎ ‎∵a＞0，∴f′（x）＞0，故f（x）在（0，＋∞）上是单调递增函数．‎ ‎（Ⅱ）由（Ⅰ）可知，．‎ ‎①若a≥－1，则x＋a≥0，即f′（x）≥0在上恒成立，‎ 此时f（x）在上为增函数，‎ ‎∴，∴（舍去）；‎ ‎②若a≤－e，则x＋a≤0，即f′（x）≤0在上恒成立，‎ 此时f（x）在上为减函数，‎ ‎∴，∴（舍去）‎ ‎③若－e＜a＜－1，令f′（x）＝0得x＝－a，‎ 当－a＜x＜e时，f′（x）＞0，∴f（x）在（－a，e）上为增函数，‎ 当1＜x＜－a时，f′（x）＜0，∴f（x）在（1，－a）上为减函数，‎ ‎∴，‎ ‎∴‎ 综上所述，．‎ ‎21．解：（Ⅰ）∵x2＝2py，∴．∴代入得 ‎∴，代点A到得t＝4．‎ ‎∴椭圆E：，a＝2，b＝1，∴，∴离心率．‎ ‎（Ⅱ）依题意，直线l的斜率必存在，设直线l的方程为y＝k（x－2），M（x1，y1），N（x2，y2）．‎ 因为，所以 所以切线l1，l2的斜率分别为，．‎ 当l1⊥l2时，，即x1x2＝－2．‎ 由得，‎ 所以，解得．‎ 又恒成立，‎ 所以存在直线l的方程是，即．‎ ‎22．解：（Ⅰ）∵x2＋y2＝ρ2，x＝ρcosθ，y＝ρsinθ，‎ ‎∴曲线C的极坐标方程为ρ＝2sinθ．‎ ‎（Ⅱ）将直线l的参数方程化为直角坐标方程，得．‎ 令y＝0，得x＝2，即M点的坐标为（2，0）．‎ 又曲线C为圆，圆C的圆心坐标为（0，1），半径r＝1，则．‎ ‎∴．‎ ‎，∴范围是．‎ ‎23．解：（Ⅰ）．‎ ‎∴2x＋1＞5，x＞2，－2x－1＞5，x＜－3．‎ 得f（x）＞5的解集为{x|x＜－3或x＞2}．‎ ‎（Ⅱ）∵f（x）＝|x－1|＋|x＋2|≥3‎ ‎∴f（x）≥a2－2a，化为a2－2a≤3‎ ‎∴－1≤a≤3即a∈‎