2018-2019学年河北省石家庄市高二上学期期末考试数学（文）试题（解析版）

2018-2019学年河北省石家庄市高二上学期期末考试数学（文）试题（解析版）

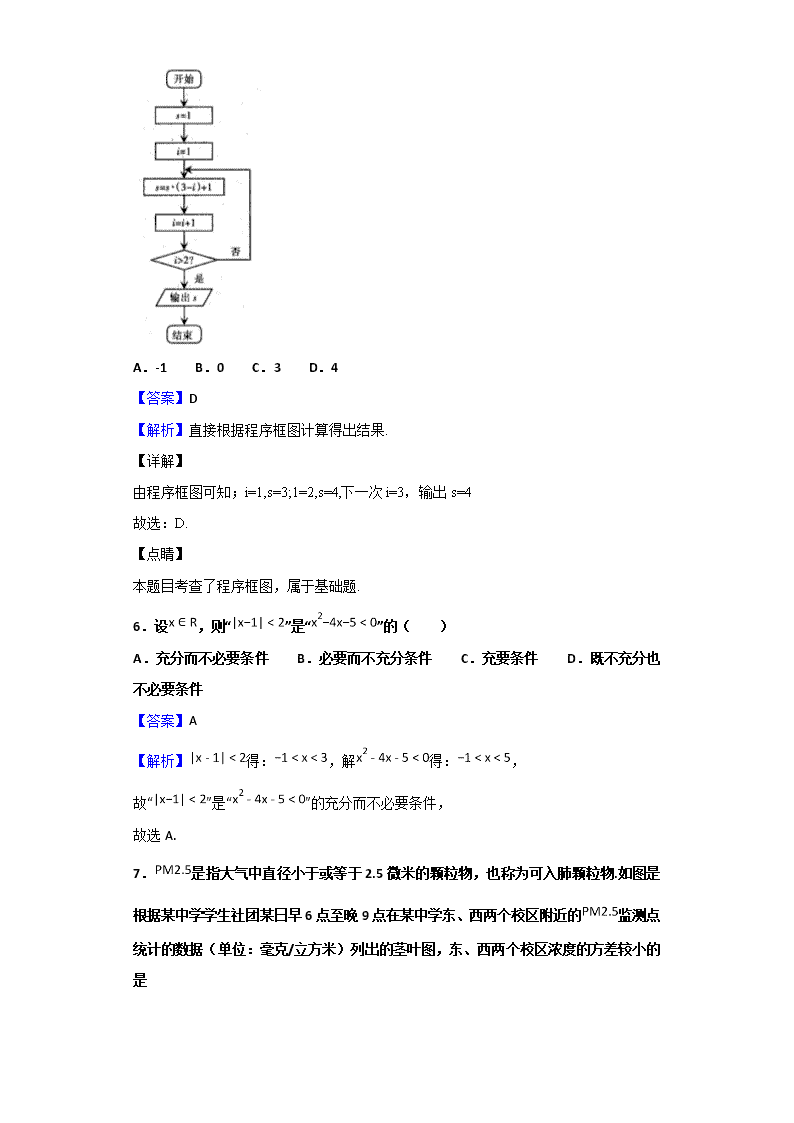
‎2018-2019学年河北省石家庄市高二上学期期末考试数学（文）试题 一、单选题 ‎1．命题“若则”的逆否命题是（ ）‎ A．若则 B．若则 C．若则 D．若则 ‎【答案】B ‎【解析】本题主要考查命题及其关系。逆否命题是将原命题的条件与结论否定，然后再将否定后的条件和结论互换，故命题“若则”的逆否命题是“若，则”。故选 ‎2．一个年级有22个班，每个班同学从1～50排学号，为了交流学习经验，要求每班学号为19的学生留下进行交流，这里运用的是 A．分层抽样法 B．抽签法 C．随机数表法 D．系统抽样法 ‎【答案】D ‎【解析】根据系统抽样的定义进行判断即可．‎ ‎【详解】‎ 每个班同学以1﹣50排学号，要求每班学号为19的同学留下来交流，‎ 则数据之间的间距差相同，都为50，‎ 所以根据系统抽样的定义可知，这里采用的是系统抽样的方法．‎ 故选：D．‎ ‎【点睛】‎ 本题主要考查抽样的定义和应用，要求熟练掌握简单抽样，系统抽样和分层抽样的定义，以及它们之间的区别和联系，比较基础．‎ ‎3．抛物线的焦点坐标是 A． B． C． D．‎ ‎【答案】B ‎【解析】先将方程化简为标准形式，即可得焦点坐标．‎ ‎【详解】‎ 由抛物线可得x2＝4y，故焦点坐标为（0，1）‎ 故选：B．‎ ‎【点睛】‎ 本题主要考查抛物线的简单性质，属于基础题．‎ ‎4．已知命题：，；命题：，，则下列说法中正确的是 A．是假命题 B．是真命题 C．是真命题 D．是假命题 ‎【答案】C ‎【解析】先判断命题的真假，进而求得复合命题真假判断真值表得到答案.‎ ‎【详解】‎ 命题p，，即命题p为真，‎ 对命题q，去 ，所以命题q为假，为真 所以是真命题 ‎ 故选：C.‎ ‎【点睛】‎ ‎(1)对于一些简单命题，判断为真，许推理证明，若判断为假，只需找出一个反例即可；‎ ‎(2)对于复合命题的真假判断应利用真值表；‎ ‎(3)也可以利用“互为逆否命题”的等价性，通过判断其逆否命题的真假来判断原命题的真假.‎ ‎5．阅读下边的程序框图，运行相应的程序，则输出的值为 A．-1 B．0 C．3 D．4‎ ‎【答案】D ‎【解析】直接根据程序框图计算得出结果.‎ ‎【详解】‎ 由程序框图可知；i=1,s=3;1=2,s=4,下一次i=3，输出s=4‎ 故选：D.‎ ‎【点睛】‎ 本题目考查了程序框图，属于基础题.‎ ‎6．设，则“”是“”的（ ）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】A ‎【解析】得：，解得：， 故“”是“”的充分而不必要条件， 故选A.‎ ‎7．是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物.如图是根据某中学学生社团某日早6点至晚9点在某中学东、西两个校区附近的监测点统计的数据（单位：毫克/立方米）列出的茎叶图，东、西两个校区浓度的方差较小的是 A．东校区 B．西校区 C．东、西两个校区相等 D．无法确定 ‎【答案】A ‎【解析】根据茎叶图得数据分布，即可得到两地浓度的方差大小.‎ ‎【详解】‎ 根据茎叶图可知，东校区数据集中在0.06和0.07之间，数据分布比较稳定；‎ 而西校区则分布比较分散，不如东校区集中，‎ 所以东校区方差较小.‎ 故选：A.‎ ‎【点睛】‎ 本题目考查了统计图中茎叶图，以及方差代表的是数据的稳定性，注意不能去计算，这样费时费力，属于中等偏下题目.‎ ‎8．方程有实根的概率为 A． B． C． D．‎ ‎【答案】A ‎【解析】根据方程有实根△≥0，得到a的范围，利用几何概型的概率求法解答．‎ ‎【详解】‎ 方程有实根，‎ 则△＝4﹣4a2≥0，解得﹣1≤a≤1，a∈[﹣1，2]的区间长度为3，‎ a∈[﹣1，1]的区间长度为2，‎ 所以方程x2+2x+a2＝0（a∈[﹣1，2]）有实根的概率为，‎ 故选：A．‎ ‎【点睛】‎ 本题考查了几何概型的概率求法；几何概型的概率的值是通过长度、面积、和体积的比值得到．‎ ‎9．圆与直线的位置关系 A．相切 B．相离 C．相交 D．不能确定 ‎【答案】C ‎【解析】据题意，先求出直线过定点（1,1），再判断出点与圆的位置关系，可得直线与圆的位置关系.‎ ‎【详解】‎ 直线化简为 ‎ ‎ 易知直线过定点(1,1)‎ 而 知点在圆内 直线与圆相交.‎ 故选：C.‎ ‎【点睛】‎ 本题目考查直线过定点的问题以及点与圆的位置关系，注意没必要联立方程解方程组，然后用判别式来求解，这样子运算量较大，属于中档题.‎ ‎10．设函数，则在区间上的最大值为（ ）‎ A．-1 B．0 C． D．‎ ‎【答案】B ‎【解析】，有。令，解得， （舍去）.当变化时， 和的变化情况如下：‎ ‎1‎ ‎-‎ ‎0‎ ‎+‎ ‎0‎ 极小值 ‎0‎ 所以当或时， 有最大值0.故选 ‎11．某人在微信群中发了一个8元“拼手气”红包，被甲、乙、丙三人抢完，若三人均领到整数元，且每人至少领到1元，则甲领到的钱数不少于其他任何人的概率为 A． B． C． D．‎ ‎【答案】B ‎【解析】利用隔板法得到共计有n21种领法，利用列举法求得甲领到的钱数不少于其他任何人的情况总数m＝8，由此能求出结果．‎ ‎【详解】‎ 如下图，利用隔板法，‎ 得到共计有n21种领法，‎ 甲领3元“甲领取的钱数不少于其他任何人”的情况有2种，即乙领3元，丙领2元或丙领3元，乙领2元，记为（乙2，丙3）或（丙2，乙3）；‎ 甲领4元“甲领取的钱数不少于其他任何人”的情况有3种，即（乙1，丙3）或（丙1，乙3）或（乙2，丙2）‎ 甲领5元“甲领取的钱数不少于其他任何人”的情况有2种，即（乙1，丙2）或（丙1，乙2）；‎ 甲领6元“甲领取的钱数不少于其他任何人”的情况只有1种，即（乙1，丙1）‎ ‎“甲领取的钱数不少于其他任何人”的情况总数m＝2+3+2+1＝6，‎ ‎∴甲领取的钱数不少于其他任何人的概率p．‎ 故选B．‎ ‎【点睛】‎ 本题考查概率的求法，考查隔板法等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．‎ ‎12．已知离心率为的双曲线的右焦点为，为坐标原点，以 为直径的圆与双曲线的一条渐近线相交于、两点.若的面积为2，则实数的值为 A．2 B． C．4 D．8‎ ‎【答案】B ‎【解析】利用双曲线离心率求出渐近线方程，利用三角形面积，结合离心率即可得到方程组求出a即可.‎ ‎【详解】‎ 因为双曲线的右焦点为，为坐标原点，以为直径的圆与双曲线的一条渐近线相交于、两点,所以，‎ ‎ ‎ 所以三角形面积 ‎ 双曲线离心率 ‎ 解得 ‎ 故选：B.‎ ‎【点睛】‎ 本题考查了双曲线的性质渐近线，离心率以及圆的相关知识，是一道较为综合的题型，必须掌握好圆锥曲线等相关知识点，属于中档题.‎ 二、填空题 ‎13．命题“，”的否定是__________．‎ ‎【答案】，‎ ‎【解析】根据特征命题的否定为全称命题，求得结果.‎ ‎【详解】‎ 命题“，”是特征命题 所以其否定命题： ‎ 故答案为：‎ ‎【点睛】‎ 本题考查了命题的否定，特征命题的否定是全称命题，属于基础题.‎ ‎14．曲线在处的切线方程是__________．‎ ‎【答案】‎ ‎【解析】试题分析：，，且，所以所求切线方程为，即．‎ ‎【考点】导数的几何意义．‎ ‎15．椭圆的两个焦点分别为、，以为边作正三角形，若椭圆恰好平分三角形的另两边，则该椭圆的离心率为__________．‎ ‎【答案】‎ ‎【解析】设椭圆与正三角形另两条边的交点分别是A，B，‎ 由题设条件知AF1=AB=BF2=c，∠F1AF2=90°， ‎ ‎ ‎ 故答案为：．‎ 点睛：这个题目考查的是椭圆的离心率的求法；将几何图形的特点和圆锥曲线联系到一起。求离心率的常用方法有：定义法，根据椭圆或者双曲线的定义列方程；数形结合的方法，利用图形的几何特点构造方程；利用点在曲线上，将点的坐标代入方程，列式子。‎ ‎16．设为抛物线：的焦点，过作直线交抛物线于、两点，为坐标原点，则面积的最小值为__________．‎ ‎【答案】‎ ‎【解析】由抛物线的焦点坐标，设直线AB的方程，代入抛物线方程，利用韦达定理，弦长公式及点到直线的距离公式，求得面积的表达式，求得最小值．‎ ‎【详解】‎ 根据题意，抛物线的焦点为F（，0）．‎ 由题意知直线AB的斜率不为0，可设直线AB的方程为x＝my+，‎ 由消去x，得y2y-9＝0，‎ 设A（x1，y1）、B（x2，y2），‎ 由根与系数的关系可得y1+y2，y1y2＝-9．‎ ‎∴丨AB丨••,‎ O到直线AB的距离d，‎ 则△OAB的面积S丨AB丨•d•••，‎ ‎∴m＝0时，S最小为，‎ 故答案为．‎ ‎【点睛】‎ 本题考查直线与抛物线的位置关系，考查韦达定理，弦长公式及点到直线距离公式的应用，考查计算能力，属于中档题．‎ ‎17．某校100名高二学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：，，，，.‎ ‎（Ⅰ）求图中的值；‎ ‎（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分.‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】（Ⅰ）由频率分布直方图得，概率之和为1求得a；‎ ‎（Ⅱ）累加各组组中值与频率的成绩可估得平均值.‎ ‎【详解】‎ 解析：（Ⅰ）依题意，得，‎ 解得.‎ ‎（Ⅱ）这100名学生语文成绩的平均分为 ‎ .‎ ‎【点睛】‎ 本题考查了对频率分布直方图的认识，以及平均数的求法，属于基础题.‎ 三、解答题 ‎18．已知命题：，命题：，若是的必要不充分条件，求实数的取值范围.‎ ‎【答案】‎ ‎【解析】根据￢p是￢q的必要不充分条件得出是的必要不充分条件，从而求出a的取值范围．‎ ‎【详解】‎ 由是的必要不充分条件，则是的必要不充分条件，‎ 从而有：‎ 解得：‎ ‎∴实数的取值范围是.‎ ‎【点睛】‎ 本题利用考查了充分、必要条件，也考查了不等式的解法与应用问题，是基础题目．‎ ‎19．已知圆过点和，且圆心在直线上.‎ ‎（1）求圆的标准方程；‎ ‎（2）求直线：被圆截得的弦长.‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】（Ⅰ）设出圆心坐标和圆的标准方程，将点带入求出结果即可；‎ ‎（Ⅱ）利用圆心到直线的距离和圆的半径解直角三角形求得弦长.‎ ‎【详解】‎ 解：（Ⅰ）由题意可设圆心坐标为，则圆的标准方程为，‎ ‎∴‎ 解得 故圆的标准方程为.‎ ‎（Ⅱ）圆心到直线的距离，‎ ‎∴‎ 直线被圆截得的弦长为.‎ ‎【点睛】‎ 本题考查了圆的方程，以及直线与圆相交求弦长的知识，属于基础题.‎ ‎20．随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ 时间代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎（1）求关于的回归方程 ‎（2）用所求回归方程预测该地区2018年（）的人民币储蓄存款.‎ ‎（参考公式： ，，）‎ ‎【答案】（1）（2）10.8‎ ‎【解析】分析：（1）先求出，，，根据回归直线方程的求法求出b的值，再代入，，求出的值即可。‎ ‎（2）由回归直线方程，代入t的值预测。‎ 详解：（1）由题意，，，，，‎ ‎∴，，∴关于的回归方程.‎ ‎（2）时，（千亿元）.‎ 点睛：本题考查了回归直线方程的求法及简单应用，对计算能力要求较高，细心耐心计算，属于简单题。‎ ‎21．已知点，椭圆的离心率为，是椭圆的右焦点，直线的斜率为，为坐标原点.‎ ‎（1）求的方程；‎ ‎（2）设过点的动直线与相交于两点，问：是否存在直线，使以为直径的圆经过原点，若存在，求出对应直线的方程，若不存在，请说明理由.‎ ‎【答案】（1）；（2）或.‎ ‎【解析】试题分析：（1）设出，由直线的斜率为求得，结合离心率求得，再由隐含条件求得，则椭圆方程可求；（2）当轴时，不合题意；当直线斜率存在时，设直线：代入椭圆方程化简，由判别式大于求得的范围，若存在以为直径的圆经过点原点，求出，即，得到，符合，进一步求出值，则直线方程可求得.‎ 试题解析：(1)设，由条件知， ，得.‎ 又，所以，‎ ‎.‎ 故的方程为.‎ ‎(2)当垂直于轴时不合题意，故设，.‎ 将代入，得．‎ 当，即时，‎ ‎，，‎ 所以．‎ 若存在以为直径的圆经过点原点，则，‎ 即，即，‎ 所以，符合，所以存在，符合题意，‎ 此时或.‎ ‎22．已知，函数（，为自然对数的底数）.‎ ‎（Ⅰ）当时，求函数的单调递增区间；‎ ‎（Ⅱ）若函数在上单调递增，求的取值范围.‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】（Ⅰ）求得a=2的函数f(x)的导数，利用导数的正负求出原函数的单调区间；‎ ‎（Ⅱ）原函数在上单调递增，即导函数在(-1,1)大于等于0恒成立，在解不等式求得a的范围.‎ ‎【详解】‎ ‎（Ⅰ）当时，.‎ 令，解得 所以，函数的单调递增区间为.‎ ‎（Ⅱ）方法1：若函数在上单调递增，则在上恒成立.‎ 即，令.‎ 则在上恒成立.‎ 只需，得：‎ 方法2：，令，即，‎ 解得.‎ 所以，的增区间为 又因为在上单调递增，所以 ‎ 即，解得.‎ ‎【点睛】‎ 本题目考查了导函数的应用，函数单调性的求法以及二次函数恒成立问题，属于中档题.‎