2017届高考文科数学(全国通用)二轮文档讲义:第2编专题2-2-1函数的图象与性质
专题二 函数与导数
第一讲 函数的图象与性质
[必记公式及概念]
1.指数与对数式的七个运算公式
(1)am·an=am+n;
(2)(am)n=amn;
(3)loga(MN)=logaM+logaN(a>0且a≠1,M>0,N>0);
(4)loga=logaM-logaN(a>0且a≠1,M>0,N>0);
(5)logaMn=nlogaM(a>0且a≠1,M>0);
(6)alogaN=N(a>0且a≠1,N>0);
(7)logaN=(a>0且a≠1,b>0且b≠1,M>0,N>0).
2.单调性定义
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,且x1
f(x2)成立,则f(x)在D上是减函数).
3.奇偶性定义
对于定义域内的任意x(定义域关于原点对称),都有f(-x)=-f(x)成立,则f(x)为奇函数(都有f(-x)=f(x)成立,则f(x)为偶函数).
4.周期性定义
周期函数f(x)的最小正周期T必须满足下列两个条件:
(1)当x取定义域内的每一个值时,都有f(x+T)=f(x);
(2)T是不为零的最小正数.
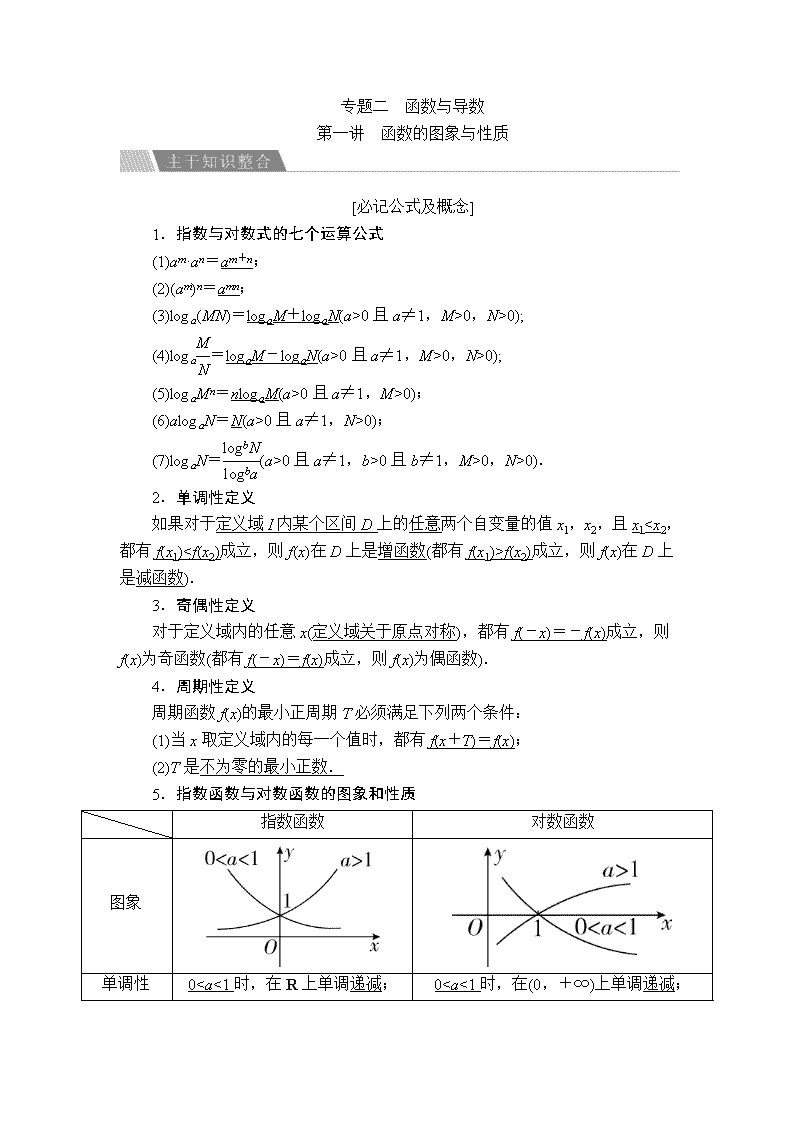
5.指数函数与对数函数的图象和性质
指数函数
对数函数
图象
单调性
01时,在R上单调递增
01时,在(0,+∞)上单调递增
续表
指数函数
对数函数
函数值
性质
00时,01
01时,y<0;
当00
a>1,
当x>0时,y>1;
当x<0时,01
当x>1时,y>0;
当00)或向右(a<0)平移|a|个单位得到y=f(x+a)的图象;
将y=f(x)的图象向上(a>0)或向下(a<0)平移|a|个单位得到y=f(x)+a的图象.
(2)对称变换
①作y=f(x)关于y轴的对称图象得到y=f(-x)的图象;
②作y=f(x)关于x轴的对称图象得到y=-f(x)的图象;
③作y=f(x)关于原点的对称图象得到y=-f(-x)的图象;
④将y=f(x)在x轴下方的图象翻折到上方,与y=f(x)在x轴上方的图象合起来得到y=|f(x)|的图象;
⑤将y=f(x)在y轴左侧部分去掉,再作右侧关于y轴的对称图象合起来得到y=f(|x|)的图象.
4.函数的周期性与对称性的关系
(1)若f(x)的图象有两条对称轴x=a和x=b(a≠b),则f(x)必为周期函数,且它的一个周期是2|b-a|;
(2)若f(x)的图象有两个对称中心(a,0)和(b,0)(a≠b),则f(x)必为周期函数,且它的一个周期是2|b-a|;
(3)若f(x)的图象有一条对称轴x=a和一个对称中心(b,0)(a≠b),则f(x)必为周期函数,且它的一个周期是4|b-a|.
[失分警示]
1.函数具有奇偶性时,定义域关于原点对称,但定义域关于原点对称时,函数不一定具有奇偶性.
2.求单调区间易忽略函数的定义域,切记单调区间必须是定义域的子集且当同增(减)区间不连续时,不能用并集符号连接.
3.忽略函数的单调性、奇偶性、周期性的定义中变量取值的任意性.
4.画图时容易忽略函数的性质,图象左右平移时平移距离的确定易出错.
考点 函数的概念及其表示
典例示法
典例1 (1)[2014·山东高考]函数f(x)=的定义域为( )
A. B.(2,+∞)
C.∪(2,+∞) D.∪[2,+∞)
[解析] 要使函数f(x)有意义,需使(log2x)2-1>0,即(log2x)2>1,∴log2x>1或log2x<-1,解之得x>2或00,b>0,c<0 B.a<0,b>0,c>0
C.a<0,b>0,c<0 D.a<0,b<0,c<0
[解析] ∵f(x)=的图象与x,y轴分别交于N,M,且点M的纵坐标与点N的横坐标均为正,∴x=->0,y=>0,故a<0,b>0,又函数图象间断点的横坐标为正,∴-c>0,故c<0,故选C.
[答案] C
1.作函数图象的方法及注意点
常用描点法和图象变换法.图象变换法常用的有平移变换、伸缩变换和对称变换.尤其注意y=f(x)与y=f(-x),y=-f(x),y=-f(-x),y=f(|x|),y=|f(x)|及y=af(x)+b的相互关系.
2.辨识函数图象的两种方法
(1)直接根据函数解析式作出函数图象,或者是根据图象变换作出函数的图象;
(2)利用间接法排除、筛选错误与正确的选项,可以从如下几个方面入手:
①从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;
②从函数的单调性,判断图象的变化趋势;
③从函数的奇偶性,判断图象的对称性:如奇函数在对称的区间上单调性一致,偶函数在对称的区间上单调性相反;
④从函数的周期性,判断图象的循环往复;
⑤从特殊点出发,排除不符合要求的选项.
灵活应用上述方法,可以很快判断出函数的图象.
3.函数图象在方程、不等式中的应用策略
(1)研究两函数图象的交点个数:在同一坐标系中分别作出两函数的图象,数形结合求解;
(2)确定方程根的个数:当方程与基本函数有关时,可以通过函数图象来研究方程的根,方程f(x)=0的根就是函数f(x)图象与x轴的交点的横坐标,方程f(x)=g(x)的根就是函数f(x)与g(x)图象交点的横坐标;
(3)研究不等式的解:当不等式问题不能用代数法求解但其对应函数的图象可作出时,常将不等式问题转化为两函数图象的上、下关系问题,从而利用数形结合求解.
针对训练
1.[2016·贵州七校联考]已知函数f(x)的图象如图所示,则f(x)的解析
式可以是( )
A.f(x)=
B.f(x)=
C.f(x)=-1
D.f(x)=x-
答案 A
解析 由函数图象可知,函数f(x)为奇函数,应排除B、C.若函数为f(x)=x-,则x→+∞时,f(x)→+∞,排除D,故选A.
2.[2016·江西南昌二模]现有四个函数:①y=xsinx,②y=xcosx,③y=x|cosx|,④y=x·2x的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
A.④①②③ B.①④③②
C.③④②① D.①④②③
答案 D
解析 由于函数y=xsinx是偶函数,由图象知,函数①对应第一个图象;函数y=xcosx为奇函数,且当x=π时,y=-π<0,故函数②对应第三个图象;函数y=x|cosx|为奇函数,故函数③与第四个图象对应;函数y=x·2x为非奇非偶函数,与第二个图象对应.综上可知,选D.
考点 函数的性质及应用
典例示法
题型1 函数性质的判定
典例3 [2015·广东高考]下列函数中,既不是奇函数,也不是偶函数的是( )
A.y= B.y=x+
C.y=2x+ D.y=x+ex
[解析] 选项A中的函数是偶函数;选项B中的函数是奇函数;选项C中的函数是偶函数;只有选项D中的函数既不是奇函数也不是偶函数.
[答案] D
题型2 函数性质的应用
典例4 [2015·天津高考]已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数.记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
A.a0,f′(1)=4-e>0,f′(2)=8-e2>0,所以存在x0∈是函数f(x)的极小值点,即函数f(x)在(0,x0)上单调递减,在(x0,2)上单调递增,且该函数为偶函数,符合条件的图象为D.
2.[2016·全国卷Ⅱ]已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则 (xi+yi)=( )
A.0 B.m
C.2m D.4m
答案 B
解析 因为f(x)+f(-x)=2,y==1+,所以函数y=f(x)与y=的图象都关于点(0,1)对称,所以xi=0,yi=×2=m,故选B.
3.[2015·全国卷Ⅰ]若函数f(x)=xln (x+)为偶函数,则a=________.
答案 1
解析 解法一:由题意得f(x)=xln (x+)=f(-x)=-xln (-x),所以+x=,解得a=1.
解法二:由f(x)为偶函数有ln (x+)为奇函数,令g(x)=ln (x+),有g(-x)=-g(x),以下同解法一.
[其它省市高考题借鉴]
4.[2016·山东高考]已知函数f(x)的定义域为R.当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>时,f=f.则f(6)=( )
A.-2 B.-1
C.0 D.2
答案 D
解析 由题意可知,当-1≤x≤1时,f(x)为奇函数,且当x>时,f(x+1)=f(x),所以f(6)=f(5×1+1)=f(1).而f(1)=-f(-1)=-[(-1)3-1]=2,所以f(6)=2.故选D.
5.[2015·浙江高考]存在函数f(x)满足:对于任意x∈R都有( )
A.f(sin2x)=sinx B.f(sin2x)=x2+x
C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|
答案 D
解析 通过举反例排除.本题主要考查函数的概念,即对于任一变量x有唯一的y与之相对应.对于A、B,当x=或时,sin2x均为1,而sinx与x2+x此时均有两个值,故A,B错误;对于C,当x=1或-1时,x2+1=2,而|x+1|有两个值,故C错误,故选D.
6.[2015·湖南高考]设函数f(x)=ln (1+x)-ln (1-x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
答案 A
解析 由题意可得,函数f(x)的定义域为(-1,1),且f(x)=ln =ln ,易知y=-1在(0,1)上为增函数,故f(x)在(0,1)上为增函数,又f(-x)=ln (1-x)-ln (1+x)=-f(x),故f(x)为奇函数,选A.
一、选择题
1.[2016·山东莱芜模拟]已知函数f(x)的定义域为[3,6],则函数y=的定义域为( )
A. B.
C. D.
答案 B
解析 要使函数y=有意义,需满足
⇒⇒≤x<2.故选B.
2.[2014·湖南高考]已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )
A.-3 B.-1
C.1 D.3
答案 C
解析 令x=-1得,f(-1)-g(-1)=(-1)3+(-1)2+1=1.∵f(x),g(x)分别是偶函数和奇函数,
∴f(-1)=f(1),g(-1)=-g(1),
即f(1)+g(1)=1.故选C.
3.[2014·全国卷Ⅰ]设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.f(x)g(x)是偶函数 B.|f(x)|g(x)是奇函数
C.f(x)|g(x)|是奇函数 D.|f(x)g(x)|是奇函数
答案 C
解析 由题意可知f(-x)=-f(x),g(-x)=g(x),对于选项A,f(-x)·g(-x)=-f(x)·g(x),所以f(x)g(x)是奇函数,故A项错误;对于选项B,|f(-x)|g(-x)=|-f(x)|g(x)=|f(x)|g(x),所以|f(x)|g(x)是偶函数,故B项错误;对于选项C,f(-x)|g(-x)|=-f(x)|g(x)|,所以f(x)|g(x)|是奇函数,故C项正确;对于选项D,|f(-x)·g(-x)|=|-f(x)g(x)|=|f(x)g(x)|,所以|f(x)g(x)|是偶函数,故D项错误,选C.
4.[2016·辽宁实验中学月考]函数y=f(x)在[0,2]上单调递增,且函数f(x+2)是偶函数,则下列结论成立的是( )
A.f(1)0,由此可排除B,故选D.
6.[2016·湖北黄冈一模]已知函数f(x)=|log2x|,正实数m,n满足m1.
又f(x)在[m2,n]上的最大值为2,由图象知:f(m2)>f(m)=f(n),
∴f(x)max=f(m2),x∈[m2,n].
故f(m2)=2,易得n=2,m=.
7.如图,过单位圆O上一点P作圆O的切线MN,点Q为圆O上一动点,当点Q由点P逆时针方向运动时,设∠POQ=x,弓形PRQ的面积为S,则S=f(x)在x∈[0,2π]上的大致图象是( )
答案 B
解析 S=f(x)=S扇形PRQ+S△POQ=(2π-x)·12+sinx=π-x+sinx,则f′(x)=(cosx-1)≤0,所以函数S=f(x)在[0,2π]上为减函数,当x=0和x=2π时,分别取得最大值与最小值.又当x从0逐渐增大到π时,cosx逐渐减小,切线斜率逐渐减小,曲线越来越陡;当x从π逐渐增大到2π时,cosx逐渐增大,切线斜率逐渐增大,曲线越来越平缓.结合选项可知,B正确.
8.[2016·辽宁五校第二次联考]已知f(x)是定义在R上的偶函数,在区间[0,+∞)上为增函数,且f=0,则不等式f(logx)>0的解集为( )
A. B.(2,+∞)
C.∪(2,+∞) D.∪(2,+∞)
答案 C
解析 由已知f(x)在R上为偶函数,且f=0,
∴f(logx)>0等价于f(|logx|)>f.
又f(x)在[0,+∞)上为增函数,
∴|logx|>,即logx>或logx<-,
解得02,故选C.
二、填空题
9.[2015·山东高考]已知函数f(x)=ax+b(a>0,a≠1)的定义域和值域都是[-1,0],则a+b=________.
答案 -
解析 ①当01时,函数f(x)在[-1,0]上单调递增,由题意可得即显然无解.
所以a+b=-.
10.[2016·浙江杭州模拟]已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+1)=;②函数y=f(x+1)的图象关于y轴对称;③对于任意的x1,x2∈[0,1],且x1f(x2).则f,f(2),f(3)从小到大排列是________.
答案 f(3)0.回答下列问题:
(1)判断f(x)在(-1,1)上的奇偶性,并说明理由;
(2)判断函数f(x)在(0,1)上的单调性,并说明理由;
(3)若f=,试求f-f-f的值.
解 (1)令x=y=0⇒f(0)=0,
令y=-x,则f(x)+f(-x)=0⇒f(-x)=-f(x)⇒f(x)在(-1,1)上是奇函数.
(2)设00,
故-1<<0,则f>0,
即当0f(x2),
∴f(x)在(0,1)上单调递减.
(3)由于f-f=f+f
=f=f.
同理,f-f=f,
f-f=f,
∴f-f-f=2f=2×=1.
12.函数f(x)是定义在R上的偶函数,且对任意实数x,都有f(x+1)=f(x-1)成立,已知当x∈[1,2]时,f(x)=logax.
(1)求x∈[-1,1]时,函数f(x)的表达式;
(2)求x∈[2k-1,2k+1](k∈Z)时,函数f(x)的表达式;
(3)若函数f(x)的最大值为,在区间[-1,3]上,解关于x的不等式f(x)>.
解 (1)因为f(x+1)=f(x-1),且f(x)是R上的偶函数,所以f(x+2)=f(x),
所以f(x)=
(2)当x∈[2k-1,2k]时,
f(x)=f(x-2k)=loga(2+x-2k),
同理,当x∈(2k,2k+1]时,
f(x)=f(x-2k)=loga(2-x+2k),
所以f(x)=
(3)由于函数是以2为周期的周期函数,故只需要考查区间[-1,1],
当a>1时,由函数f(x)的最大值为,
知f(0)=f(x)max=loga2=,即a=4,
当0,所以-2,
所以0的解集为(,4-),
综上所述不等式的解集为(-2,2-)∪(,4-).