2013江西卷(文)数学试题
2013·江西卷(文科数学)
1. 复数z=i(-2-i)(i为虚数单位)在复平面内所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
1.D [解析] z=1-2i,故选D.
2. 若集合A={x∈|ax2+ax+1=0}中只有一个元素,则a=( )
A.4 B.2 C.0 D.0或4
2.A [解析] 当a=0时,A=∅;当a≠0时,Δ=a2-4a=0,则a=4,故选A.
3. 若sin=,则cos α=( )
A.- B.-
C. D.
3.C [解析] cos α=1-2sin2 =,故选C.
4. 集合A={2,3},B={1,2,3}, 从A,B中各任意取一个数,则这两数之和等于4的概率是( )
A. B.
C. D.
4.C [解析] 从A,B中任取一个数,共有6种取法,其中两数之和为4的是(2,2),(3,1),故P==,故选C.
5. 总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08 B.07
C.02 D.01
5.D [解析] 选出来的5个个体编号依次为:08,02,14,07,01.故选D.
6. 下列选项中,使不等式x<
0⇒x<0或x>1,求交集得x<-1,故选A.
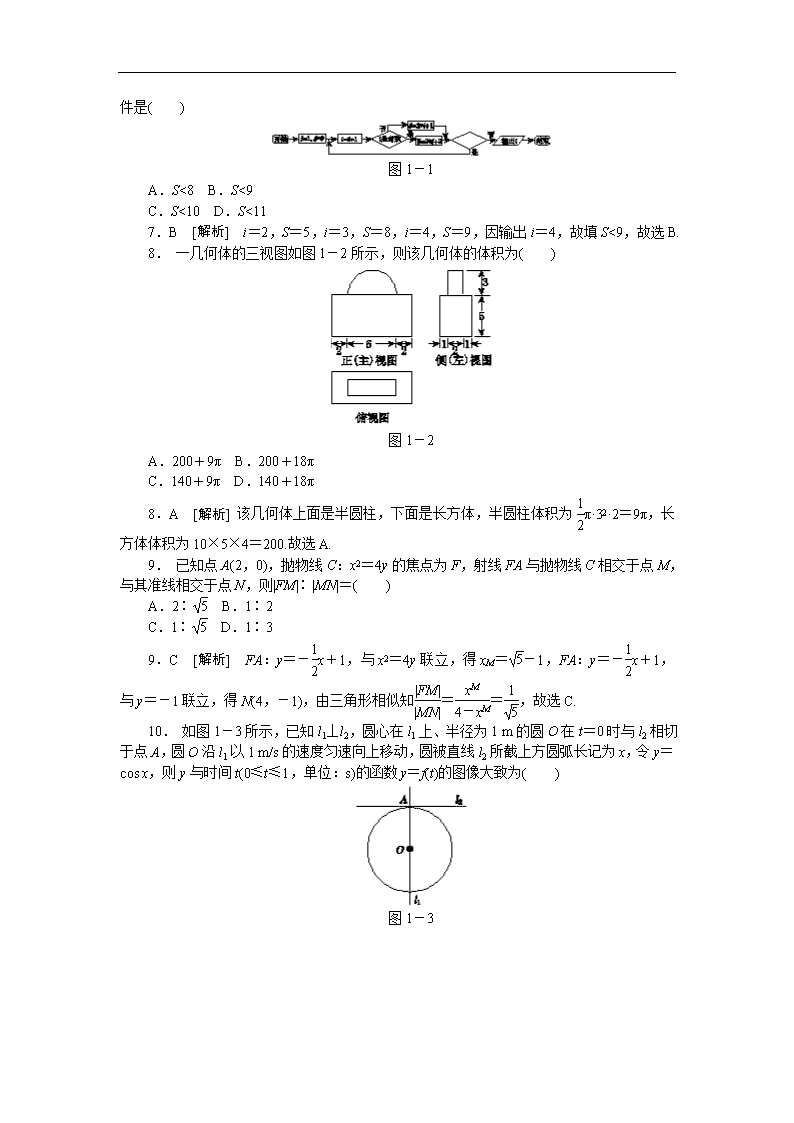
7. 阅读如图1-1所示的程序框图,如果输出i
=4,那么空白的判断框中应填入的条件是( )
图1-1
A.S<8 B.S<9
C.S<10 D.S<11
7.B [解析] i=2,S=5,i=3,S=8,i=4,S=9,因输出i=4,故填S<9,故选B.
8. 一几何体的三视图如图1-2所示,则该几何体的体积为( )
图1-2
A.200+9π B.200+18π
C.140+9π D.140+18π
8.A [解析] 该几何体上面是半圆柱,下面是长方体,半圆柱体积为π·32·2=9π,长方体体积为10×5×4=200.故选A.
9. 已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|=( )
A.2∶ B.1∶2
C.1∶ D.1∶3
9.C [解析] FA:y=-x+1,与x2=4y联立,得xM=-1,FA:y=-x+1,与y=-1联立,得N(4,-1),由三角形相似知==,故选C.
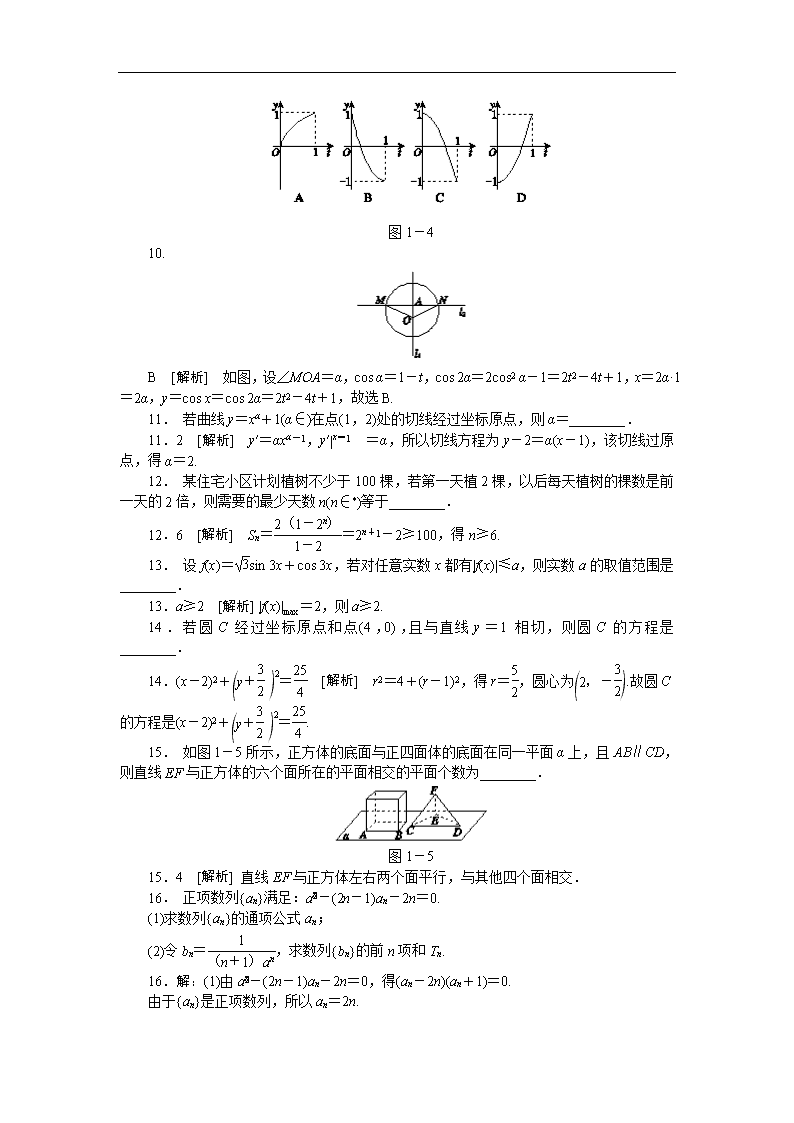
10. 如图1-3所示,已知l1⊥l2,圆心在l1上、半径为1 m的圆O在t=0时与l2相切于点A,圆O沿l1以1 m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=cos x,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图像大致为( )
图1-3
图1-4
10.
B [解析] 如图,设∠MOA=α,cos α=1-t,cos 2α=2cos2 α-1=2t2-4t+1,x=2α·1=2α,y=cos x=cos 2α=2t2-4t+1,故选B.
11. 若曲线y=xα+1(α∈)在点(1,2)处的切线经过坐标原点,则α=________.
11.2 [解析] y′=αxα-1,y′=α,所以切线方程为y-2=α(x-1),该切线过原点,得α=2.
12. 某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵数是前一天的2倍,则需要的最少天数n(n∈*)等于________.
12.6 [解析] Sn==2n+1-2≥100,得n≥6.
13. 设f(x)=sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
13.a≥2 [解析] |f(x)|max=2,则a≥2.
14. 若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是________.
14.(x-2)2+= [解析] r2=4+(r-1)2,得r=,圆心为.故圆C的方程是(x-2)2+=.
15. 如图1-5所示,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.
图1-5
15.4 [解析] 直线EF与正方体左右两个面平行,与其他四个面相交.
16. 正项数列{an}满足:a-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an;
(2)令bn=,求数列{bn}的前n项和Tn.
16.解:(1)由a-(2n-1)an-2n=0,得(an-2n)(an+1)=0.
由于{an}是正项数列,所以an=2n.
(2)由an=2n,bn=,则bn==,
Tn=
==.
17. 在△ABC中,角A,B,C的对边分别为a,b,c,已知sin Asin B+sin Bsin C+cos 2B=1.
(1)求证:a,b,c成等差数列;
(2)若C=,求的值.
17.解:(1)证明:由题意得sin Asin B+sin Bsin C=2sin2 B,
因为sin B≠0,所以sin A+sin C=2sin B,
由正弦定理,有a+c=2b,即a,b,c成等差数列.
(2)由C=,c=2b-a及余弦定理得(2b-a)2=a2+b2+ab,
即有5ab-3b2=0,所以=.
18. 小波以游戏方式决定是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图1-6)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋.
(1)写出数量积X的所有可能取值;
(2)分别求小波去下棋的概率和不去唱歌的概率.
图1-6
18.解:(1)X的所有可能取值为-2,-1,0,1.
(2)数量积为-2的有·,共1种;
数量积为-1的有·,·,·,·,·,·,共6种;
数量积为0的有·,·,·,·,共4种;
数量积为1的有·,·,·,·,共4种.
故所有可能的情况共有15种.
所以小波去下棋的概率为P1=;
因为去唱歌的概率为P2=,所以小波不去唱歌的概率P=1-P2=1-=.
19., 如图1-7所示,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3.
(1)证明:BE⊥平面BB1C1C;
(2)求点B1到平面EA1C1的距离.
图1-7
19.解:(1)证明:过B作CD的垂线交CD于F,则BF=AD=,EF=AB-DE=1,FC=2.
在Rt△BEF中,BE=.
在Rt△CFB中,BC=.
在△BEC中,因为BE2+BC2=9=EC2,故BE⊥BC.
由BB1⊥平面ABCD得BE⊥BB1.
所以BE⊥平面BB1C1C.
(2)三棱锥E-A1B1C1的体积V=·AA1·S△A1B1C1=.
在Rt△A1D1C1中,A1C1==3 .
同理,EC1==3 ,A1E==2 .
故S△A1C1E=3 .
设点B1到平面EA1C1的距离为d,则三棱锥B1-A1C1E的体积
V=·d·S△A1C1E=d,
从而d=,d=.
20., 椭圆C:+=1(a>b>0)的离心率e=,a+b=3.
(1)求椭圆C的方程;
(2)如图1-8所示,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.
证明:2m-k为定值.
图1-8
20.解:(1)因为e==,
所以a=c,b=c,代入a+b=3得,c=,a=2,b=1,
故椭圆C的方程为+y2=1.
(2)方法一:因为B(2,0),P不为椭圆顶点,则直线BP的方程为y=k(x-2),①
①代入+y2=1,解得P.
直线AD的方程为y=x+1.②
①与②联立解得M.
由D(0,1),P,N(x,0)三点共线知
=,解得N.
所以MN的斜率为m===,
则2m-k=-k=(定值).
方法二:
设P(x0,y0)(x0≠0,±2),则k=.
直线AD的方程为:y=(x+2),
直线BP的方程为:y=(x-2),
直线DP的方程为:y-1=x,令y=0,由于y0≠1可得N,
联立
解得M,
因此MN的斜率为
m==
==.
所以2m-k=-
=
=
=
=(定值).
21., 设函数
f(x)=a为常数且a∈(0,1).
(1)当a=时,求f;
(2)若x0满足f(f(x0))=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f(f(x1))),B(x2,f(f(x2))),C(a2,0),记△ABC的面积为S(a),求S(a)在区间上的最大值和最小值.
21.解:(1)当a=时,f=,
f=f=2=.
(2)f(f(x))=
当0≤x≤a2时,由x=x解得x=0,
因为f(0)=0,故x=0不是f(x)的二阶周期点;
当a20.
(或令g(a)=a3-2a2-2a+2,
g′(a)=3a2-4a-2=3,
因a∈(0,1),g′(a)<0,则g(a)在区间上的最小值为g=>0,
故对于任意a∈,g(a)=a3-2a2-2a+2>0,
S′(a)=·>0)
则S(a)在区间上单调递增,
故S(a)在区间上的最小值为S=,最大值为S=.