高考数学【理科】真题分类详细解析版专题5 三角函数（原卷版）

高考数学【理科】真题分类详细解析版专题5 三角函数（原卷版）

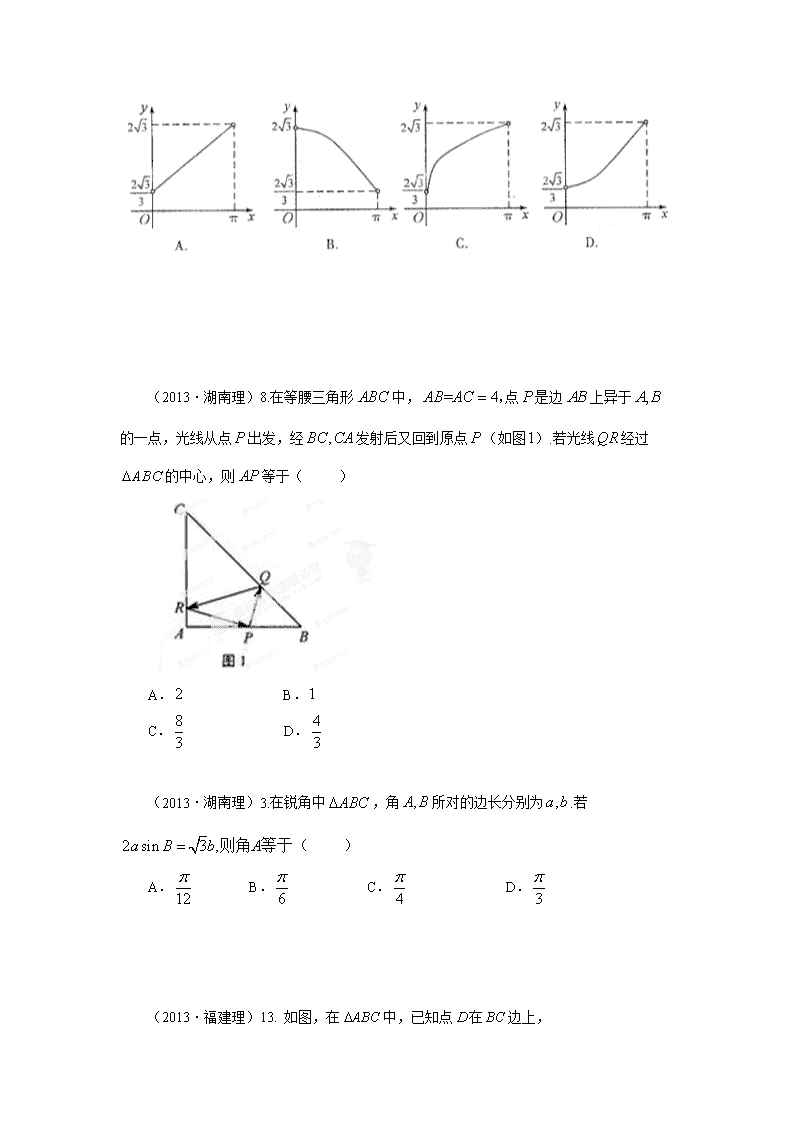
专题05 三角函数 ‎【2013高考真题】‎ ‎（2013·新课标I理）15、设当x=θ时，函数f(x)＝sinx－2cosx取得最大值，则cosθ=______‎ ‎（2013·浙江理）6.已知，则（ ）‎ A. B. C. D.‎ ‎（2013·天津理）6. 在△ABC中, 则 = （ ）‎ ‎ (A) (B) (C) (D) ‎ ‎（2013·上海理）11．若，‎ 则 ‎（2013·上海理）4．已知△ABC的内角A、B、C所对应边分别为a、b、c，若，则角C的大小是_______________（结果用反三角函数值表示）‎ ‎（2013·陕西理）7. 设△ABC的内角A, B, C所对的边分别为a, b, c, 若, 则△ABC的形状为 （ ）‎ ‎ (A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定 ‎（2013·山东理）5.将函数的图象沿轴向左平移个单位后，得到一 个偶函数的图象，则的一个可能取值为 A. B. C. D. ‎ ‎（2013·辽宁理）（9）已知点 A． B． ‎ C． D．‎ ‎（2013·辽宁理）（6）在，内角所对的边长分别为 A． B． C． D． ‎ ‎（2013·江西理） 11．函数y=sin2x+2sin2x的最小正周期T为_______.‎ ‎（2013·新课标Ⅱ理）（15）设θ为第二象限角，若tan（θ+）=，则sinθ+cosθ=_________.‎ ‎（2013·江西理）10.如图，半径为1的半圆O与等边三角形ABC夹在两平行线，之间//,与半圆相交于F,G两点，与三角形ABC两边相交于Ｅ，Ｄ两点，设弧的长为，，若从平行移动到，则函数的图像大致是 ‎[ ‎ ‎ ‎ ‎（2013·湖南理）8.在等腰三角形中，点是边上异于的一点，光线从点出发，经发射后又回到原点（如图）.若光线经过的中心，则等于（ ）‎ A． B． ‎ C． D． ‎ ‎（2013·湖南理）3.在锐角中，角所对的边长分别为.若（ ）‎ A． B． C． D． ‎ ‎（2013·福建理）13. 如图，在中，已知点在边上，‎ ‎,, , 则的长为_____ ‎ ‎（2013·大纲理）13.已知是第三象限角，，则 ‎ ‎（2013·大纲理）12.已知函数，下列结论中错误的是（ ）‎ A．的图像关于点中心对称 ‎ B．的图像关于直线对称 C．的最大值为 ‎ ‎ D．既是奇函数，又是周期函数 ‎（2013·北京理）15. (本小题共13分)在△ABC中，a=3，b=2，∠B=2∠A.‎ ‎(I)求cosA的值； ‎ ‎ (II)求c的值.‎ ‎（2013·浙江理）16. 中，,是的中点，若，则________。‎ ‎（2013·安徽理）（12）设的内角所对边的长分别为。若，则则角_________.‎ ‎（2013·安徽理）（16）（本小题满分12分）‎ 已知函数 的最小正周期为。‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）讨论在区间上的单调性。‎ ‎（2013·新课标Ⅱ理）（17）（本小题满分12分）‎ ‎△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB。‎ ‎（Ⅰ）求B；‎ ‎（Ⅱ）若b=2，求△ABC面积的最大值。‎ ‎（2013·大纲理）18.（本小题满分12分）‎ 设的内角A、B、C的对边分别为a、b、c，.‎ ‎（Ⅰ）求B；‎ ‎（Ⅱ）若，求C.‎ ‎（2013·福建理）20.（本小题满分14分）‎ 已知函数的周期为，图象的一个对称中心为，将函数图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将得到的图象向右平移个单位长度后得到函数的图象。‎ （1） 求函数与的解析式 （2） 是否存在，使得按照某种顺序成等差数列？若存在，请确定的个数，若不存在，说明理由；‎ （1） 求实数与正整数，使得在内恰有2013个零点 ‎（2013·广东理）16．（本小题满分12分）‎ 已知函数,.‎ ‎(Ⅰ) 求的值； ‎ ‎ (Ⅱ) 若,,求．‎ ‎（2013·湖南理）17．（本小题满分12分）已知函数。‎ ‎（I）若是第一象限角，且。求的值；‎ ‎（II）求使成立的x的取值集合。‎ ‎（2013·江西理）16．（本小题满分12分）‎ 在△ABC中，角A，B，C所对的边分别为a，b，c，已知 ‎（1）求角B的大小；‎ ‎（2）若a+c=1，求b的取值范围.‎ ‎（2013·辽宁理）17．（本小题满分12分）‎ 设向量 ‎（I）若 ‎（II）设函数 ‎（2013·辽宁理）22．（本小题满分10分）选修4-1：几何证明选讲 如图，‎ ‎（I）‎ ‎（II）‎ ‎（2013·山东理）17.设的内角所对的边分别为，且，。‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求的值。‎ ‎（2013·陕西理）16. (本小题满分12分)‎ 已知向量, 设函数. ‎ ‎ (Ⅰ) 求f (x)的最小正周期. ‎ ‎ (Ⅱ) 求f (x) 在上的最大值和最小值. ‎ ‎（2013·上海理）21．（6分+8分）已知函数，其中常数；‎ ‎（1）若在上单调递增，求的取值范围；‎ ‎（2）令，将函数的图像向左平移个单位，再向上平移1个单位，得到函数的图像，区间（且）满足：在上至少含有30个零点，在所有满足上述条件的中，求的最小值．‎ ‎（2013·天津理）15． (本小题满分13分)‎ 已知函数. ‎ ‎(Ⅰ) 求f(x)的最小正周期; ‎ ‎(Ⅱ) 求f(x)在区间上的最大值和最小值. ‎ ‎【2012高考真题】‎ ‎1．（2012·湖北卷）函数f(x)＝xcosx2在区间（0,4]上的零点个数为(　　)‎ A．4 B．5‎ C．6 D．7‎ ‎2．（2012·辽宁卷）已知sinα－cosα＝，α∈(0，π)，则tanα＝(　　)‎ A．－1 B．－ C. D．1‎ ‎3．（2012·福建卷）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：‎ ‎ ‎ ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎4．（2012·重庆卷）设f(x)＝4cossinωx－cos(2ωx＋π)，其中ω＞0.‎ ‎(1)求函数y＝f(x)的值域；‎ ‎(2)若f(x)在区间上为增函数，求ω的最大值．‎ ‎5．（2012·广东卷）已知函数f(x)＝2cos(其中ω>0，x∈R)的最小正周期为10π.‎ ‎(1)求ω的值；‎ ‎(2)设α，β∈，f＝－，f＝，求cos(α＋β)的值．‎ ‎7．（2012·湖南卷）函数f(x)＝sin(ωx＋φ)的导函数y＝f′(x)的部分图象如图1－5所示，其中，P为图象与y轴的交点，A，C为图象与x轴的两个交点，B为图象的最低点．‎ ‎(1)若φ＝，点P的坐标为，则ω＝________；‎ ‎(2)若在曲线段与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为________．‎ 图1－5‎ ‎8．（2012·北京卷）已知函数f(x)＝.‎ ‎(1)求f(x)的定义域及最小正周期；‎ ‎(2)求f(x)的单调递增区间．‎ ‎9．（2012·山东卷）已知向量m＝(sinx,1)，n＝(A>0)，函数f(x)＝m·n的最大值为6.‎ ‎(1)求A；‎ ‎(2)将函数y＝f(x)的图象向左平移个单位，再将所得图象上各点的横坐标缩短为原来的倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)在上的值域．‎ ‎10．（2012·陕西卷） 函数f(x)＝Asin＋1(A>0，ω>0)的最大值为3，其图像相邻两条对称轴之间的距离为.‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)设α∈，f＝2，求α的值．‎ ‎12．（2012·陕西卷）函数f(x)＝Asin＋1(A>0，ω>0)的最大值为3，其图像相邻两条对称轴之间的距离为.‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)设α∈，f＝2，求α的值．‎ ‎13．（2012·安徽卷）设函数f(x)＝cos2x＋＋sin2x.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)设函数g(x)对任意x∈R，有g＝g(x)，且当x∈时，g(x)＝－f(x)．求g(x)在区间（－π，0]上的解析式．‎ ‎15．（2012·全国卷）当函数y＝sinx－cosx(0≤x<2π)取得最大值时，x＝________.‎ ‎16．（2012·湖北卷）已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx,2 cosωx)．设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈.‎ ‎(1)求函数f(x)的最小正周期；‎ ‎(2)若y＝f(x)的图象经过点，求函数f(x)在区间上的取值范围．‎ ‎17．（2012·课标全国卷）已知ω>0，函数f(x)＝sin在单调递减，则ω的取值范围是(　　)‎ A. B. C. D．(0,2]‎ ‎18．（2012·浙江卷）把函数y＝cos2x＋1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，然后向左平移1个单位长度，再向下平移1个单位长度，得到的图象是(　　)‎ 图1－1‎ ‎19．（2012·重庆卷）设tanα，tanβ是方程x2－3x＋2＝0的两根，则tan(α＋β)的值为(　　)‎ A．－3 B．－‎1 C．1 D．3‎ ‎20．（2012·课标全国卷）已知a，b，c分别为△ABC三个内角A，B，C的对边，acosC＋asinC－b－c＝0.‎ ‎(1)求A；‎ ‎(2)若a＝2，△ABC的面积为，求b，c.‎ ‎21．（2012·重庆卷）设f(x)＝4cossinωx－cos(2ωx＋π)，其中ω＞0.‎ ‎(1)求函数y＝f(x)的值域；‎ ‎(2)若f(x)在区间上为增函数，求ω的最大值．‎ ‎22．（2012·广东卷）已知函数f(x)＝2cos(其中ω>0，x∈R)的最小正周期为10π.‎ ‎(1)求ω的值；‎ ‎(2)设α，β∈，f＝－，f＝，求cos(α＋β)的值．‎ ‎23．（2012·安徽卷）在平面直角坐标系中，点O(0,0)，P(6,8)，将向量绕点O按逆时针方向旋转后得向量，则点Q的坐标是(　　)‎ ‎24．（2012·安徽卷）设函数f(x)＝cos2x＋＋sin2x.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)设函数g(x)对任意x∈R，有g＝g(x)，且当x∈时，g(x)＝－f(x)．求g(x)在区间（－π，0]上的解析式．‎ ‎25．（2012·北京卷）已知函数f(x)＝.‎ ‎(1)求f(x)的定义域及最小正周期；‎ ‎(2)求f(x)的单调递增区间．‎ ‎26．（2012·福建卷）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：‎ ‎ ‎ ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎27．（2012·江苏卷）设α为锐角，若cos＝，则sin的值为________．‎ ‎28．（2012·全国卷）已知α为第二象限角，sinα＋cosα＝，则cos2α＝(　　)‎ A．－ B．－ C. D. ‎29．（2012·安徽卷）设函数f(x)＝cos2x＋＋sin2x.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)设函数g(x)对任意x∈R，有g＝g(x)，且当x∈时，g(x)＝－f(x)．求g(x)在区间（－π，0]上的解析式．‎ ‎30．（2012·福建卷）某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：‎ ‎ ‎ ‎(5)sin2(－25°)＋cos255°－sin(－25°)cos55°.‎ ‎(1)请从上述五个式子中选择一个，求出这个常数；‎ ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎31．（2012·湖北卷）已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx,2cosωx)．设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈.‎ ‎(1)求函数f(x)的最小正周期；‎ ‎(2)若y＝f(x)的图象经过点，求函数f(x)在区间上的取值范围．‎ ‎32．（2012·山东卷）若θ∈，sin2θ＝，则sinθ＝(　　)‎ A. B. C. D. ‎33．（2012·湖南卷）函数f(x)＝sinx－cos的值域为(　　)‎ ‎34．（2012·安徽卷）设函数f(x)＝cos2x＋＋sin2x.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)设函数g(x)对任意x∈R，有g＝g(x)，且当x∈时，g(x)＝－f(x)．求g(x)在区间（－π，0]上的解析式．‎ ‎35．（2012·湖北卷）已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx,2cosωx)．设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈.‎ ‎(1)求函数f(x)的最小正周期；‎ ‎(2)若y＝f(x)的图象经过点，求函数f(x)在区间上的取值范围．‎ ‎36．（2012·江西卷）若tanθ＋＝4，则sin2θ＝(　　)‎ A. B. C. D. ‎37．（2012·重庆卷）设tanα，tanβ是方程x2－3x＋2＝0的两根，则tan(α＋β)的值为(　　)‎ A．－3 B．－‎1 C．1 D．3‎ ‎38．（2012·重庆卷）设△ABC的内角A，B，C的对边分别为a、b、c，且cosA＝，cosB＝，b＝3，则c＝________.‎ ‎39．（2012·四川卷）如图1－1所示，正方形ABCD的边长为1，延长BA至E，使AE＝1，连结EC、ED，则sin∠CED＝(　　)‎ 图1－1‎ A. B. C. D. ‎40．（2012·上海卷）在△ABC中，若sin‎2A＋sin2B＜sin‎2C，则△ABC的形状是(　　)‎ A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定 ‎41．（2012·江西卷）在△ABC中，角A，B，C的对边分别为a，b，c.已知A＝，bsin－csin＝a.‎ ‎(1)求证：B－C＝；‎ ‎(2)若a＝，求△ABC的面积．‎ ‎42．（2012·辽宁卷）在△ABC中，角A，B，C的对边分别为a，b，c.角A，B，C成等差数列．‎ ‎(1)求cosB的值；‎ ‎(2)边a，b，c成等比数列，求sinAsinC的值．‎ ‎43．（2012·全国卷）△ABC的内角A、B、C的对边分别为a、b、c，已知cos(A－C)＋cosB＝1，a＝‎2c，求C.‎ ‎44．（2012·北京卷）在△ABC中，若a＝2，b＋c＝7，cosB＝－，则b＝________.‎ ‎45．（2012·湖北卷）设△ABC的内角A，B，C所对的边分别为a，b，c.若(a＋b－c)(a＋b＋c)＝ab，则角C＝________.‎ ‎46．（2012·浙江卷）在△ABC中，M是BC的中点，AM＝3，BC＝10，则·＝________.‎ ‎47．（2012·浙江卷）在△ABC中，内角A，B，C的对边分别为a，b，c.已知cosA＝，sinB＝cosC.‎ ‎(1)求tanC的值；‎ ‎(2)若a＝，求△ABC的面积．‎ ‎48．（2012·湖南卷）在△ABC中，AB＝2，AC＝3，·＝1，则BC＝(　　)‎ A. B. C．2 D. ‎49．（2012·陕西卷）在△ABC中，角A，B，C所对边的长分别为a，b，c，若a2＋b2＝‎2c2，则cosC的最小值为(　　)‎ A. B. C. D．－ ‎50．（2012·课标全国卷）已知a，b，c分别为△ABC三个内角A，B，C的对边，acosC＋asinC－b－c＝0.‎ ‎(1)求A；‎ ‎(2)若a＝2，△ABC的面积为，求b，c.‎ ‎51．（2012·安徽卷）设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的是________(写出所有正确命题的编号)．‎ ‎52．（2012·福建卷）已知△ABC的三边长成公比为的等比数列，则其最大角的余弦值为________．‎ ‎53．（2012·天津卷）在△ABC中，内角A，B，C所对的边分别是a，b，c.已知8b＝‎5c，C＝2B，则cosC＝(　　)‎ A. B．－ C．± D. ‎54．（2012·天津卷）已知函数f(x)＝sin＋sin＋2 cos2x－1，x∈R.‎ ‎(1)求函数f(x)的最小正周期；‎ ‎(2)求函数f(x)在区间上的最大值和最小值．‎ ‎55．（2012·四川卷）函数f(x)＝6cos2＋sinωx－3(ω＞0)在一个周期内的图象如图1－5所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．‎ 图1－5‎ ‎(1)求ω的值及函数f(x)的值域；‎ ‎(2)若f(x0)＝，且x0∈，求f(x0＋1)的值．‎ ‎56．（2012·江苏卷）在△ABC中，已知·＝3·.‎ ‎(1)求证：tanB＝3tanA；‎ ‎(2)若cosC＝，求A的值．‎ ‎57．（2012·浙江卷）在△ABC中，内角A，B，C的对边分别为a，b，c.已知cosA＝，sinB＝cosC.‎ ‎(1)求tanC的值；‎ ‎(2)若a＝，求△ABC的面积．‎ ‎58．（2012·陕西卷）在△ABC中，角A，B，C所对边的长分别为a，b，c，若a2＋b2＝‎2c2，则cosC的最小值为(　　)‎ A. B. C. D．－ ‎59．（2012·山东卷）如图1－4所示，在平面直角坐标系xOy 中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P的位置在(0,0)，圆在x轴上沿正向滚动，当圆滚动到圆心位于(2,1)时，的坐标为________．‎ 图1－4‎ ‎【2011高考真题精选】‎ ‎ 1.(2011年高考安徽卷理科9)已知函数，其中为实数，若对恒成立，且，则的单调递增区间是 ‎（A） （B）‎ ‎（C） （D）‎ ‎2.(2011年高考辽宁卷理科4)△ABC的三个内角A、B、C所对的边分别为a，b，c，asin AsinB+bcos‎2A=则（ ）‎ ‎ (A) (B) (C) (D)‎ ‎3.(2011年高考辽宁卷理科7)设sin，则（ ）‎ ‎(A) (B) (C) (D)‎ ‎4.(2011年高考浙江卷理科6)若，，，‎ ‎，则 ‎（A） （B） （C） （D）‎ ‎5．(2011年高考陕西卷理科6)函数在内 ‎ ‎（A）没有零点 （B）有且仅有一个零点 ‎ ‎（C）有且仅有两一个零点（D）有无穷个零点 ‎6.(2011年高考重庆卷理科6)若的内角所对的边满足，且，则的值为 ‎（A） (B) ‎ ‎(C)1 (D) ‎ ‎7.(2011年高考辽宁卷理科16)已知函数f（x）=Atan（x+）（＞0，），y=f（x）的部分图像如下图，则f（）=____________.‎ ‎8.(2011年高考安徽卷理科14)已知 的一个内角为120o，并且三边长构成公差为4的等差数列，则的面积为_______________‎ ‎9.(2011年高考重庆卷理科14)已知，且，则的值为 ‎ ‎10.(2011年高考全国卷理科14)已知a∈(，)，sinα=，则tan2α=‎ ‎11.(2011年高考安徽卷江苏7)已知 则的值为__________‎ ‎12．(2011年高考上海卷理科8)函数的最大值为 。‎ ‎13. (2011年高考山东卷理科17)（本小题满分12分）‎ 在ABC中，内角A，B，C的对边分别为a，b，c.已知.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若cosB=，,求的面积.‎ ‎14. (2011年高考天津卷理科15)（本小题满分13分）‎ 已知函数，‎ ‎（Ⅰ）求的定义域与最小正周期；‎ ‎（Ⅱ）设，若求的大小．‎ ‎15. (2011年高考江西卷理科17)（本小题满分12分）‎ 在△ABC中，角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin ‎ ‎（1）求sinC的值 ‎（2）若 a2+b2=4(a+b)-8，求边c的值 ‎17. (2011年高考广东卷理科16)（本小题满分12分）‎ 已知函数 ‎（1）求的值；‎ ‎（2）设求的值.‎ ‎18. (2011年高考湖北卷理科16)（本小题满分10分）‎ 设△ABC的内角A、B、C所对的边分别为，已知.‎ ‎(Ⅰ) 求△ABC的周长；‎ ‎(Ⅱ)求cos(A—C.)‎ ‎19．(2011年高考陕西卷理科18)（本小题满分12分）叙述并证明余弦定理 ‎20.(2011年高考重庆卷理科16)（本小题满分13分）‎ 设满足，求函数 在 上的最大值和最小值 ‎21. (2011年高考四川卷理科17)（本小题共12分）‎ 已知函数 ‎.‎ ‎22.(2011年高考全国卷理科17) (本小题满分l0分)(注意：在试题卷上作答无效)‎ ‎ △ABC的内角A、B、C的对边分别为a、b、c.己知A—C=90°，a+c=b，求C.‎ ‎24．(2011年高考北京卷理科15)（本小题共13分）‎ 已知函数。‎ ‎（Ⅰ）求的最小正周期：‎ ‎（Ⅱ）求在区间上的最大值和最小值。‎ ‎【2010年高考真题精选】‎ ‎1.（2010浙江理数）（9）设函数，则在下列区间中函数不存在零点的是 ‎（A） （B） （C） （D）‎ ‎2.（2010浙江理数）（4）设，则“”是“”的 ‎（A）充分而不必要条件 （B）必要而不充分条件 ‎（C）充分必要条件 （D）既不充分也不必要条件 ‎3.（2010全国卷2理数）（7）为了得到函数的图像，只需把函数的图像 ‎（A）向左平移个长度单位 （B）向右平移个长度单位 ‎（C）向左平移个长度单位 （D）向右平移个长度单位 ‎4.（2010辽宁理数）（5）设>0,函数y=sin(x+)+2的图像向右平移个单位后与原图像重合，则的最小值是 ‎（A） (B) (C) (D)3 ‎ ‎5.（2010江西理数）.E，F是等腰直角△ABC斜边AB上的三等分点，则（ ）‎ A. B. C. D. ‎ ‎6.（2010四川理数）（6）将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是 ‎（A） （B） ‎ ‎（C） （D）‎ ‎7.（2010天津理数）在△ABC中，内角A,B,C的对边分别是a,b,c，若，，则A=‎ ‎（A） （B） （C） （D）‎ ‎8.（2010湖北理数）3.在中，a=15,b=10,A=60°，则=‎ A － B C － D ‎ ‎9.（2010福建理数）的值等于（ ）‎ A． B． C． D．‎ ‎10.（2010浙江理数）（11）函数的最小正周期是_______________‎ ‎11.（2010全国卷2理数）（13）已知是第二象限的角，，则 ．‎ ‎12.（2010广东理数）11.已知a,b,c分别是△ABC的三个内角A,B,C所对的边，若a=1,b=, A+C=2B,则sinC= .‎ ‎13.（2010福建理数）已知函数和的图象的对称轴完全相同。若，则的取值范围是 。‎ ‎14.（2010江苏卷）定义在区间上的函数y=6cosx的图像与y=5tanx的图像的交点为P，过点P作PP1⊥x轴于点P1，直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为____________。‎ ‎15.（2010江苏卷）在锐角三角形ABC，A、B、C的对边分别为a、b、c，，则=_________。‎ ‎16.（2010浙江理数）（18）(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c，已知 ‎18.（2010江西理数）17.（本小题满分12高☆考♂资♀源*网分）‎ 已知函数。‎ ‎(1) 当m=0时，求在区间上的取值范围；‎ ‎(2) 当时，，求m的值。‎ ‎19.（2010北京理数）（15）（本小题共13分）‎ ‎ 已知函数。‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求的最大值和最小值。‎ ‎20.（2010四川理数）（19）（本小题满分12分）‎ ‎（Ⅰ）证明两角和的余弦公式；‎ ‎ 由推导两角和的正弦公式.‎ ‎（Ⅱ）已知△ABC的面积，且，求cosC.‎ 本小题主要考察两角和的正、余弦公式、诱导公式、同角三角函数间的关系等基础知识及运算能力。‎ ‎22.（2010福建理数）19．（本小题满分13分）‎ ‎。，轮船位于港口O北偏西且与该港口相距20海里的A处，并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以海里/小时的航行速度匀速行驶，经过t小时与轮船相遇。‎ ‎（1）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？‎ ‎（2）假设小艇的最高航行速度只能达到‎30海里/小时，试设计航行方案（即确定航行方向与航行速度的大小），使得小艇能以最短时间与轮船相遇，并说明理由。‎ ‎23.（2010江苏卷）17、（本小题满分14分）‎ 某兴趣小组测量电视塔AE的高度H(单位：m），如示意图，垂直放置的标杆BC的高度h=‎4m，仰角∠ABE=，∠ADE=。‎ 该小组已经测得一组、的值，tan=1.24，tan=1.20，请据此算出H的值；‎ 该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使与之差较大，可以提高测量精确度。若电视塔的实际高度为‎125m，试问d为多少时，-最大？‎ ‎24.（2010江苏卷）23.（本小题满分10分）‎ 已知△ABC的三边长都是有理数。‎ 求证cosA是有理数；（2）求证：对任意正整数n，cosnA是有理数。‎ ‎【2009年高考真题精选】 ‎ ‎1．(2009·山东文理3)将函数的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ). ‎ A. B. C. D. ‎ ‎2．(2009·浙江文理8)已知是实数，则函数的图象不可能是( )‎ ‎3．(2009·天津理7)已知函数的最小正周期为，为了得到函数的图象，只要将的图象 A 向左平移个单位长度 B 向右平移个单位长度 C 向左平移个单位长度 D 向右平移个单位长度 ‎ ‎4．(2009·江苏4)函数为常数，‎ 在闭区间上的图象如图所示，则 .‎ ‎5．(2009·海南理14)已知函数(>0, )的图像如图所示，则 =________________ ‎ ‎6．(2009·安徽文理16)在△ABC中，sin(C-A)=1,sinB=.‎ ‎(Ⅰ)求sinA的值；‎ ‎(Ⅱ)设AC=，求△ABC的面积.‎ 本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识，考查运算求解能力。 ‎ ‎7.（2009·宁夏海南理15）（本小题满分12分）‎ 为了测量两山顶M，N间的距离，飞机沿水平方向在A，B两点进行测量，A，B，M，N在同一个铅垂平面内（如示意图），飞机能够测量的数据有俯角和A，B间的距离，请设计一个方案，包括：①指出需要测量的数据（用字母表示，并在图中标出）；②用文字和公式写出计算M，N间的距离的步骤。‎ ‎8．(2009·山东理17)设函数。‎ ‎(Ⅰ)求函数的最大值和最小正周期； ‎ ‎(Ⅱ)设A，B，C为的三个内角，若，且C为锐角，求。‎ ‎9．(2009·广东理16)已知向量互相垂直，其中．‎ ‎(1)求的值；‎ ‎(2)若，求的值．‎ ‎10．(2009·浙江理18)在ABC中，角A、B、C所对应的边分别为a、b、c，且满足=,‎ ‎=3.‎ ‎(Ⅰ)求三角形ABC的面积； ‎ ‎(Ⅱ)若b+c=6,求a的值。‎ ‎11．(2009·天津理17)在⊿ABC中，BC=，AC=3，sinC=2sinA ‎ ‎(I) 求AB的值： ‎ ‎(II) 求sin的值 ‎【2008年高考真题精选】‎ ‎1．(2008·山东卷)函数的图象是 ‎2．(2008·山东卷)已知，则的值是 ‎(A)-　　　　(B) (C)- (D) ‎ ‎3．(2008·山东理科卷)已知a，b，c为△ABC的三个内角A，B，C的对边，向量m＝()，n＝(cosA,sinA).若m⊥n，且acosB+bcosA=csinC，则角B＝‎ ‎.‎ ‎4．(2008·江苏卷)的最小正周期为，其中，则 。‎ ‎5．(2008·广东理科卷)已知函数，，则的最小正周期是 ．‎ ‎6．(海南、宁夏理科卷)已知函数)在区间的图像如下：那么＝( )‎ A．1 B．‎2 ‎C． D． ‎ ‎7．(2008·海南、宁夏理科卷)( ) ‎ A． B． C． D．‎ ‎9．(2008·广东卷)已知函数，的最大值是1，其图像经过点．‎ ‎(1)求的解析式；‎ ‎(2)已知，且，，求的值．‎ ‎10．(2008·江苏卷)如图，在平面直角坐标系中，以轴为始边做两个锐角，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为。‎