高考数学专题复习:课时达标检测(十一) 函数的图象及其应用
课时达标检测(十一) 函数的图象及其应用
[练基础小题——强化运算能力]
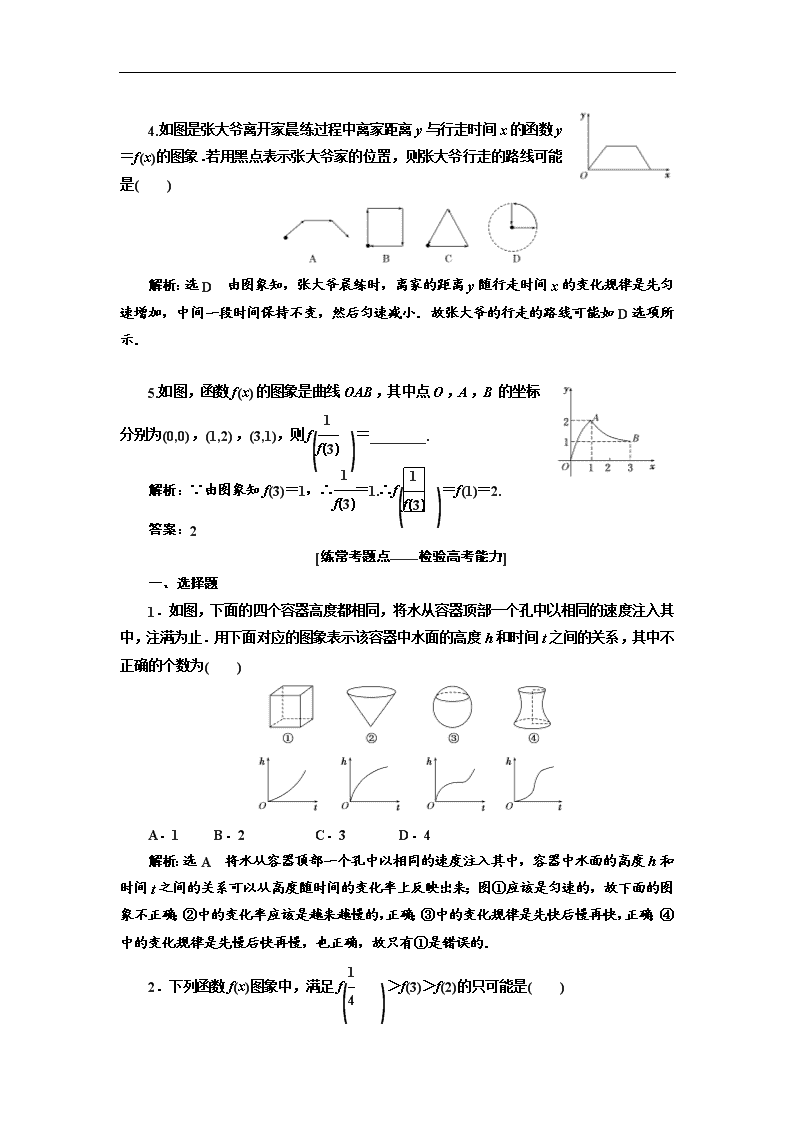
1.函数f(x)=的图象大致为( )
解析:选A 因为f(x)=,所以f(0)=f(π)=f(-π)=0,排除选项C,D;当0
0,所以当00,排除选项B,故选A.
2.已知定义在区间[0,2]上的函数y=f(x)的图象如图所示,则y=-f(2-x)的图象为( )
解析:选B 由y=f(x)的图象知,f(x)=当x∈[0,2]时,2-x∈[0,2],所以f(2-x)=故y=-f(2-x)=
3.若变量x,y满足|x|-ln=0,则y关于x的函数图象大致是( )
解析:选B 由|x|-ln=0,得y==利用指数函数图象可知选B.
4.如图是张大爷离开家晨练过程中离家距离y与行走时间x的函数y
=f(x)的图象.若用黑点表示张大爷家的位置,则张大爷行走的路线可能是( )
解析:选D 由图象知,张大爷晨练时,离家的距离y随行走时间x的变化规律是先匀速增加,中间一段时间保持不变,然后匀速减小.故张大爷的行走的路线可能如D选项所示.
5.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f=________.
解析:∵由图象知f(3)=1,∴=1.∴f=f(1)=2.
答案:2
[练常考题点——检验高考能力]
一、选择题
1.如图,下面的四个容器高度都相同,将水从容器顶部一个孔中以相同的速度注入其中,注满为止.用下面对应的图象表示该容器中水面的高度h和时间t之间的关系,其中不正确的个数为( )
A.1 B.2 C.3 D.4
解析:选A 将水从容器顶部一个孔中以相同的速度注入其中,容器中水面的高度h和时间t之间的关系可以从高度随时间的变化率上反映出来;图①应该是匀速的,故下面的图象不正确;②中的变化率应该是越来越慢的,正确;③中的变化规律是先快后慢再快,正确;④中的变化规律是先慢后快再慢,也正确,故只有①是错误的.
2.下列函数f(x)图象中,满足f>f(3)>f(2)的只可能是( )
解析:选D 因为f>f(3)>f(2),所以函数f(x)有增有减,排除A,B.在C中,f<f(0)=1,f(3)>f(0),即f<f(3),排除C,选D.
3.函数y=的图象大致是( )
解析:选C 由题意得,x≠0,排除A;当x<0时,x3<0,3x-1<0,∴>0,排除B;又∵x→+∞时,→0,∴排除D,故选C.
4.函数f(x)=的图象如图所示,则下列结论成立的是( )
A.a>0,b>0,c<0
B.a<0,b>0,c>0
C.a<0,b>0,c<0
D.a<0,b<0,c<0
解析:选C 函数定义域为{x|x≠-c},结合图象知-c>0,∴c<0.令x=0,得f(0)=,又由图象知f(0)>0,∴b>0.令f(x)=0,得x=-,结合图象知->0,∴a<0.故选C.
5.(2017·绵阳模拟)已知函数y=f(x)及y=g(x)的图象分别如图所示,方程f(g(x))=0和g(f(x))=0的实根个数分别为a和b,则ab=( )
A.24 B.15 C.6 D.4
解析:选A 由图象知,f(x)=0有3个根,分别为0,±m(m>0),其中14或a<0时,f(x)的图象与直线y=a只有一个交点,即方程f(x)=a只有一个实数根,所以a的取值范围是(-∞,0)∪(4,+∞).
12.设函数f(x)=x+的图象为C1,C1关于点A(2,1)的对称图象为C2,C2对应的函数为g(x).
(1)求函数g(x)的解析式;
(2)若直线y=b与C2有且仅有一个公共点,求b的值,并求出交点的坐标.
解:(1)设曲线C2上的任意一点为P(x,y),则P关于A(2,1)的对称点P′(4-x,2-y)在C1上,
所以2-y=4-x+,
即y=x-2+=,
所以g(x)=(x≠4).
(2)由=b,得(x-3)2=b(x-4)(x≠4).
所以x2-(b+6)x+4b+9=0(x≠4)(*)有唯一实根.
由Δ=[-(b+6)]2-4(4b+9)=b2-4b=0,
得b=0或b=4,
把b=0代入(*)式得x=3,所以g(3)==0;
把b=4代入(*)式得x=5,所以g(5)==4,
所以当b=0或b=4时,直线y=b与C2有且仅有一个公共点,且交点的坐标为(3,0)或(5,4).